基于时间相关性的风速威布尔分布优化方法
国电联合动力技术有限公司 王果毅 牟金磊 李润祥
风资源评估及建模过程是决定宏观区域选址、机型选择、电网运行调度、容量可信度计算等工作的决定性因素。在风资源评估过程中完整年风速是各项评估的基础依据。完整年风速数据通常通过建立测风塔进行采集。而测风塔的精密部件大多长期暴露于自然环境中,测风塔的损坏会导致风速数据的缺失。
基于历史实测数据提取信息所拟合的风速概率模型为基础,通过对该概率模型进行抽样,对风速缺失部分进行补全是处理风速缺失问题的常用方法。在众多的概率密度模型中,威布尔分布以其形式简单、描述灵活等优点为业内普遍接受。威布尔分布中包含两个关键参数,通常以K 和C 表示,两参数将会在威布尔分布的仿真过程中共同影响风速分布模型的分布情况及峰值位置。在实际操作中,威布尔分布的两参数有多种求法,常用方法有最大风速法、累积分布函数拟合、平均风速法、平均风速与标准差等。
纵观上述两参数的求法,都是通过以历史实测风速的年平均值及风速标准差为基础计算得到的,因此威布尔分布在对区域风场的风速分布概率的描述中有很好的表达效果。但是传统的两参数威布尔分布在描绘风速分布时,并没有考虑风速序列相邻数值间的相互影响关系,在仿真过程中仅能参考风速分布密度得到无序的概率序列,与实际工况中存在变化规律的风速序列存在较大差异。因此传统两参数威布尔分布在对风资源的评估中依旧存在一定局限性。
若将风速视为变量,变量间的相互影响关系通常以相关性进行描述。在众多的相关性描述方法中Copula 函数形式灵活、应用广泛,在不同领域内如水文、气候、经济等方面均有良好的应用效果,因此在描述风速序列相邻数值间的相互影响关系上同样具备参考价值。
本文提供一种基于时间相关性的风速描述方法,在传统两参数风速威布尔分布的基础上,结合基于Copula 函数对风资源信息中的时间相关性信息进行提取,并基于时间相关性在基于威布尔分布对风速抽样过程进行约束。仿真证明,该方法可为风资源评估过程中的风速缺失部分提供更符合自然工况的仿真数据,对威布尔分布的建模过程有显著的优化效果,在实际工程中具备良好的应用价值。
威布尔分布及Copula 函数
风速威布尔分布
威布尔分布是在风电行业内被广泛认可的风速密度函数,其主要形式如式(1)所示。
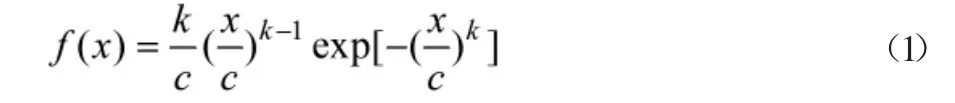
式中变量x 为风速;c 为描述风速的尺度参数;k 为描述风速分布的形状参数。C 值越大,威布尔分布所描述的风速均值越大;k 值越大,威布尔分布描述的风速分布越集中。关键参数有多种求法,其中较为常用的一种如式(2)所示。
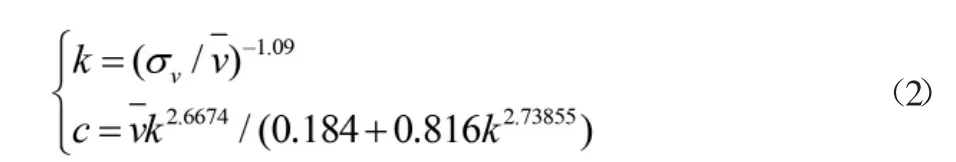

式中α 为0 到1 之间均匀分布的随机变量,x 为由α 及关键参数k 值及c 值所得到的模拟风速数值。在仿真过程中通过对α 进行随机抽样来建立风速序列。如图1 所示,该图为基于某风场威布尔分布所模拟的间隔为10 分钟、时长为一周的仿真风速,该序列所包含的风速数据有1008 个。该风速的关键参数K=2.6、C=7.45。
如图2 所示,该图为该风场的历史实测风速。
通过对比可以明显看出,相比于具有明显连续性的实测风速,基于威布尔分布所拟合的风速呈现明显的排列混乱且波动剧烈。因此,仅基于威布尔分布对风速进行模拟来补充风速的缺失部分存在明显的局限性。
Copula 函数
Copula 函数的主要功能,是反向求取多元随机变量的相关性关系,其表达形式如式(4)所示。
F(x1,x2,…,xn)=C(F1(x1),F2(x2),…,Fn(xn)) (4)
式中F(x1,x2,…,xn)为随机变量的联合分布;Fn(xn)为联合分布中第n 个变量的边缘分布;C(F1(x1),F2(x2),…,Fn(xn))为用以表达变量间相关性的Copula 函数。Copula 函数的实际原理是通过拟合随机变量的分布得到不同变量0 到1 之间均匀分布的特征值,以二元Copula 函数为例,式(5)为两个随机变量。

式中X1、X2为需要寻求相关性的随机变量,其中将x1、x2为[0.1]均匀分布的随机数,分别是X1、X2的特征值。当X1、X2表示风速时,结合式(3)可得,x1、x2分别是不同风速的α 值,f(x)、g(x)分别为不同关键参数威布尔分布的反函数。Copula函数相关性建模原理如式(6)所示。

式中K 为x1、x2基于Copula 函数相关性特性系数,x3为[0.1]均匀分布的随机数。通过对随机变量的特征值间建立函数关系,再由具备函数关系的特征值可以得到具备相关性的变量值。
由此可见,应用Copula 函数对随机变量相关性建模时充分地考虑了两变量之间的相关性及变量各自的随机性。
基于风速时间相关性的风速威布尔分布优化方法
根据上一节中的分析,基于威布尔分布的风速建模方法的局限性,主要在于对变量特征值α 的采样为随机抽样,忽略了风速序列相邻数值间的相互影响关系。
由Copula 函数对数值相关性的灵活且良好表达效果,提出基于风速时间相关性的风速威布尔分布优化方法。通过Copula 函数对风速数值间的相关性进行发掘,并结合Copula函数对风速建模过程进行优化。
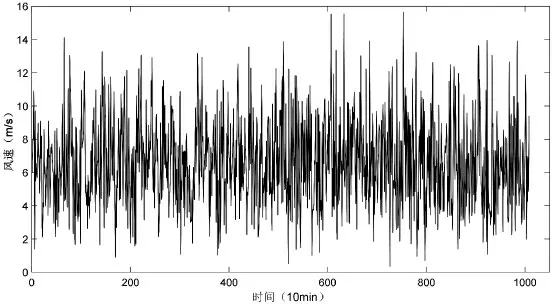
图1 基于威布尔分布的模拟风速
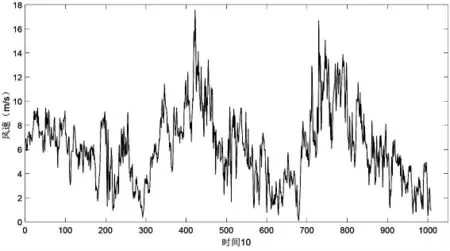
图2 历史实测风速
假设有一组风速,序列中包含(v1-vn)n 个风速数据,将风速序列需包含的数据如式(7)所示进行组合。
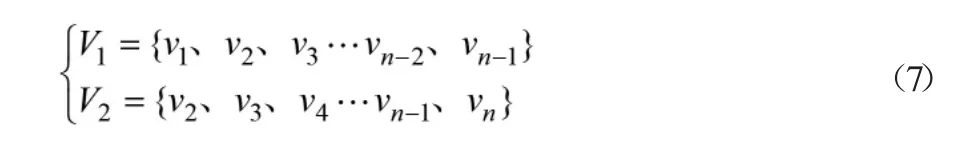
将V1 与V2 中的元素一一对应,就可以构成如式(8)所示的对应关系。

由式(8)所示的对应关系所得到的相关性关系可以认为是风速序列相邻点数值之间的相关性,即风速的时间相关性。对于相关性强弱的评估,通常以相关性系数作为评估标准,常用的相关性系数有kendall 相关性系数、spearman 相关性系数、pearson 相关性系数。由表1 所示,该表为实测数据及威布尔分布拟合的风速序列在不同类型相关性系数。

表1 不同类型相关性对比
根据表1 可以看出,实测风速具有极强的时间相关性,不同的相关性系数均达到0.8 以上,而基于威布尔分布的模拟风速相邻数据之间毫无相关性可言。因此提出基于风速时间相关性的风速威布尔分布优化方法,应用实测风速的强相关性对基于威布尔分布的风速建模过程进行约束。如式(9)~(11)所示。
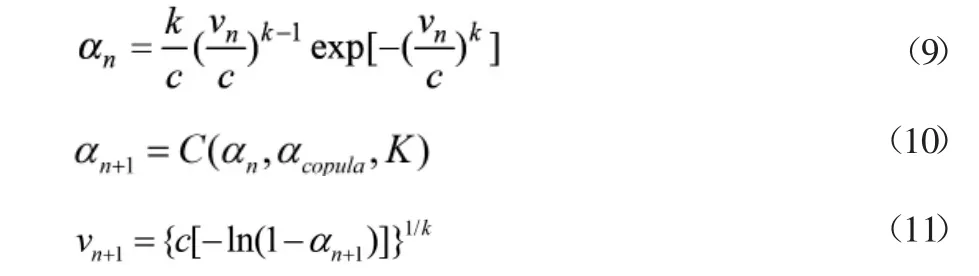
式(9)对应式(1),vn为风速序列中最后一个数据,基于威布尔分布求取该风速所对应的特征值αn。
式(10)对应式(6),基于αn及风速的时间相关性得到vn下一点需要拟合的风速vn+1所对应的特征值αn+1。
式(11)对应式(3),应用威布尔分布的反函数及由式(10)所得到的vn+1所对应的特征值αn+1共同得到风速vn+1的实际数值。
此时得到的vn+1将参考风速,根据式(9)~(11)求取vn+2。以此步骤进行循环,直至将风速的缺失部分填充完整。
综上所述,基于风速时间相关性的风速威布尔分布优化方法的流程如图3 所示。
仿真对比验证
模拟风序列的特性对比
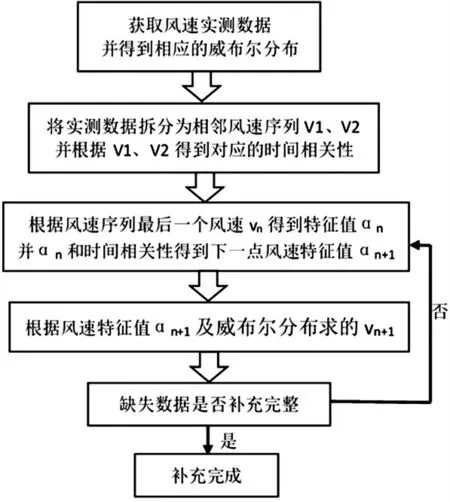
图3 基于风速时间相关性的风速威布尔分布优化方法流程

图4 基于风速时间相关性的风速威布尔分布优化方法模拟风速

表2 不同类型相关性对比
应用基于风速时间相关性的风速威布尔分布优化方法同样拟合,同样以10 分钟为间隔,时间跨度为一周,数据量为1008。模拟风速如图4 所示。
如式(7),将应用三种不同相关性系数对基于风速时间相关性的风速威布尔分布优化方法的模拟风速分为两个相邻风速序列,同样应用三种不同的相关性对两序列进行相关性评价,如表2 所示。
根据表2 所示的基于风速时间相关性的模拟风速时间相关性系数,对比表1 的两种不同风速的相关性可以看到,基于风速时间相关性的风速威布尔分布优化方法所得到的模拟风速的时间相关性更接近自然条件下实测风速的时间相关性。同样对比图4 及图1 可以看出,在时间相关性的约束下,所建立的风速具备更好的连续性及更具规律的波动性。

图5 基于风速时间相关性的风速威布尔分布优化方法模拟风速
如图5 所示,为基于风速时间相关性的风速威布尔分布优化方法的模拟风速对分布概率进行拟合的分布曲线,及实测风速对分布概率进行拟合的分布曲线进行比较。
图中虚线为实测风速的分布曲线,实线为基于风速时间相关性的风速威布尔分布优化方法的模拟风速的分布曲线。
通过图5 的对比可以得到结论,基于风速时间相关性的风速威布尔分布优化方法在对风速模拟过程优化的同时,依旧能够良好地保持风速的分布情况,该方法不仅对威布尔分布有显著的优化效果,同时对风速分布有良好的还原效果。模拟风序列的出力对比
风机出力模型如式(12)所示。

表中,V 表示风速;Vci为风机切入风速;Vco为风机切出风速;Vr表示额定风速;Pr表示风机额定功率;P(V)表示风速为V时对应的风机输出功率。风机工作中,风机功率输出如图6 所示。
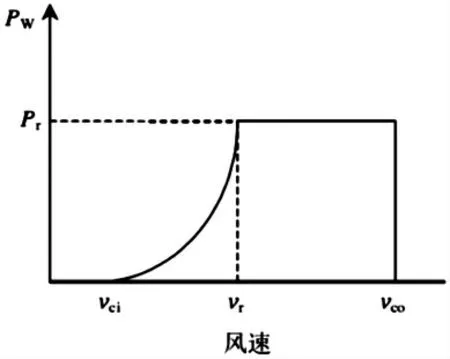
图6 风机功率输出曲线
由式(12)可知,风机出力与风速呈现三次方关系,风速的剧烈波动将会被急剧放大。如图7、图8 所示,图7 为基于威布尔分布模拟风速的风电场出力曲线,图8 为基于风速时间相关性的风速威布尔分布优化方法的模拟风速的风电场出力曲线。该风场拟采用20 台2.5 兆瓦风机。风机参数见表3。

图7 基于威布尔分布模拟风速的风电场出力曲线

表3 风机参数表
通过图7、图8 的对比可以得到结论,基于风速时间相关性的风速威布尔分布优化方法模拟风速在应用于风电场出力计算的工作中具备更好的连续性,可以更好地还原风电场的出力模式,相比于基于威布尔分布的风速模拟结果拥有更好的工程应用价值。
结论
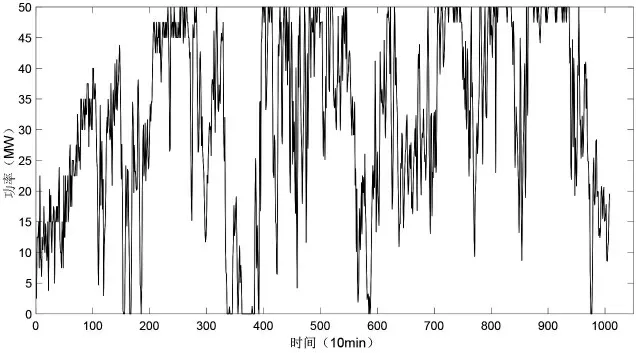
图8 基于风速时间相关性模拟风速的风电场出力曲线
风资源评估是风电工程的基础,而完整的风速数据是风资源评估工作的保障。因此,对缺失风速数据进行良好的补充,对风电工程的顺利开展具有重要意义。
基于威布尔分布的风速模拟在工程应用中依旧存在一定的缺陷,最明显的就是在对风速的模拟过程中未对风速序列的时间相关性进行充分考虑,导致所得到的风速序列波动过大、连续性差,而这个问题在对风电场出力评估的过程中将被剧烈放大。
为改善威布尔分布在风速模拟工作中的缺陷,本文提出一种基于风速时间相关性的风速威布尔分布优化方法,主要原理为应用Copula 函数对风速的时间相关性进行发掘,并用风速的时间相关性对风速模拟过程进行约束。经过仿真验证表明,该方法对风速模拟工作有巨大的改良效果,同时对风速分布依旧有良好的还原效果,可以得到还原性更好的风速仿真数据,更符合实际工程需求,在对风速理论改进的同时拥有良好的工程应用前景。

