数学课堂中教与学“擦肩而过”的现象研究——兼谈PCK的利与弊
顿继安
(北京教育学院 数学系,北京 100044)
1 问题的提出
美国学者舒尔曼(Shulman)1986年提出 PCK(Pedagogical Content Knowledge)理论,这一理论认为学科教师仅具有学科知识和教学知识是不够的,必须能够将学科知识与教学知识整合,也就是拥有特定内容,学生是怎么思维的,该怎么教的知识.PCK理论的提出源于传统教师教育中学科知识与教学知识处于相互割裂状态的情形,因此,一经提出就得到了教师教育研究者的高度关注,以PCK理论为基础,数学教育研究者提出数学教学内容知识(MPCK),既关于某一特定的数学内容该如何进行表述、呈现和解释,以使学生更容易接受和理解的知识.PCK理论强调教师能够“用学生能理解的方法来表述学科内容的知识”,这对于教师占绝对控制地位的课堂有效性的提高至关重要.
然而,中国世纪之交启动的课程改革提出“以学生为主体”,“转变学生学习方式”的要求,中小学数学课堂更强调给学生思考、探究的机会,提倡教师的教要尽可能以学生在思考与探究中表现出的智慧与困难作为教学资源,实现教师的教与学生的学的有机融合.在这样的背景下,中国中小学课堂教学实践中遇到的突出问题就是教师的预设与课堂的生成的矛盾,而这一矛盾的产生经常带来数学课堂中教与学“擦肩而过”现象的出现.像教师给了学生思考与探索的时间,但是当学生的探索与教师的预设不一致时,学生探索的方法和成果的潜在价值得不到珍视,学生的困难与问题也得不到分析和解决,此时教师教的活动并没能有效地服务于学生学的活动,这里称这一现象为教与学“擦肩而过”的现象.
研究表明,如果用PCK理论解释教与学“擦肩而过”的现象就是教师缺乏“关于特定内容的教学知识”,但是,这种解释将问题归因于表面,不利于解决教师专业发展中的根本问题.
2 两个案例
下面的两个案例分别来自五年级教师和九年级教师,是研究者根据自身亲历的两位老师的备课、上课和教师的课后研讨过程所获得的资料加以组织形成的.
案例1:最小公倍数(五年级)
授课教师背景:A老师,北京市中心城区某小学高级教师,区级骨干教师,教龄17年.
受A老师所在学校的邀请,研究者参与了A老师“最小公倍数”一课的研讨活动,经历了备课、上课、课后研讨的完整过程.
备课时,研究者建议,最小公倍数的定义是计算最小公倍数的基础,因此,定义得出后,不妨给学生一个探究的机会,让学生先利用最小公倍数的定义求出两个数的最小公倍数,然后教师组织同学一起总结规律,找到更加便捷的求最小公倍数的方法——因数分解法.
A老师接受了建议,决定尝试一下.
上课时,在得到最小公倍数的概念后,A老师首先请同学独立解决几个求最小公倍数的题目:(1)[1, 7];(2)[5, 6];(3)[9, 15];(4)[2, 8];(5)[4, 9];(6)[8, 12].
大约5分钟后,A老师组织同学进行交流.
师:你们认为哪些题目最好算?
生(齐答):第1题和第4题最好算.
师:怎么好算了?
生1:因为第1题中的1和7、第4题中的2和8有倍数关系,最小公倍数就是其中的大数.
师:我们发现了两个有倍数关系的数的最小公倍数就是其中的大数,非常好.那么,比这两个稍好算一些的呢?
生2:[5, 6]这两个数是相邻的,相邻的数相乘就是最小公倍数.
生3:不仅是[5, 6],[4, 9]=36,我认为如果两个数互质,那么最小公倍数就是两个数相乘.
师:我们又找到了一个规律,很好.[9, 15]这个题目你们是怎么算的?
生4:我用的是列举法,先列出9的倍数:9、18、36、45,发现45也是15的倍数,最小公倍数就是各自的倍数,所以9和15的最小公倍数就是45.
生 5(主动举手):老师,我慢慢发现,这种题也有简便方法,就是用最小公因数乘以大数:3×15=45……
师(打断生5):最小公因数?9和15的最小公因数是3吗?
生5:哦,是用不是1的那个最小公因数.我验证了,[8, 12]这个题目也行,它们(不是1的)的最小公因数是2,用2×12=24.
此时其他同学没有反应,A老师评论道:哦,你的发现挺好,但是对所有数都能用吗?下课你再研究研究.下面我们一起来看怎么求这种情况下的两个数的最小公倍数.
接下来,A老师向同学介绍了求最小公倍数的因数分解法.
下课后,研究者(记为D)对A老师进行了访谈:
D:你感觉怎么样?
A:开始感觉挺好的,没想到学生说得这么好,但生 5说出她的方法后就有点乱了.
D:你怎么看生5的方法?
A:我也不知道她的方法对不对,不知道该怎么办了!
D:我们来分析一下生5的方法.首先,她的发现适用范围有限,比如,对于6、12就不适用;但是既然适用于[9,15]、[8, 12],就一定有其道理,你看,对于[9, 15]=3×15,15显然是题目给的,那3从哪里来的?从9中出来的,可是9中有两个3(9=3×3),为什么只给了最小公倍数1个?另一个哪里去了?“藏”在15中了.这样,生6的发现是不是就有一般意义了:任意两个数求最小公倍数,一个数做因数,另一个数中比这个数“多”出来的因数也是最小公倍数的因数,这不就是因式分解求最小公倍数的原理吗?
A:哦!原来是这样,以前上课从没遇到过这种情况,就不知道怎么处理了.
案例2:圆周角定理(九年级)
授课教师背景:B老师,北京市某郊区中学一级教师,校级骨干教师,教龄7年.
“圆周角定理”是指:一条弧所对的圆周角等于圆心角的一半,如图1所示∠BOC=2∠BAC.
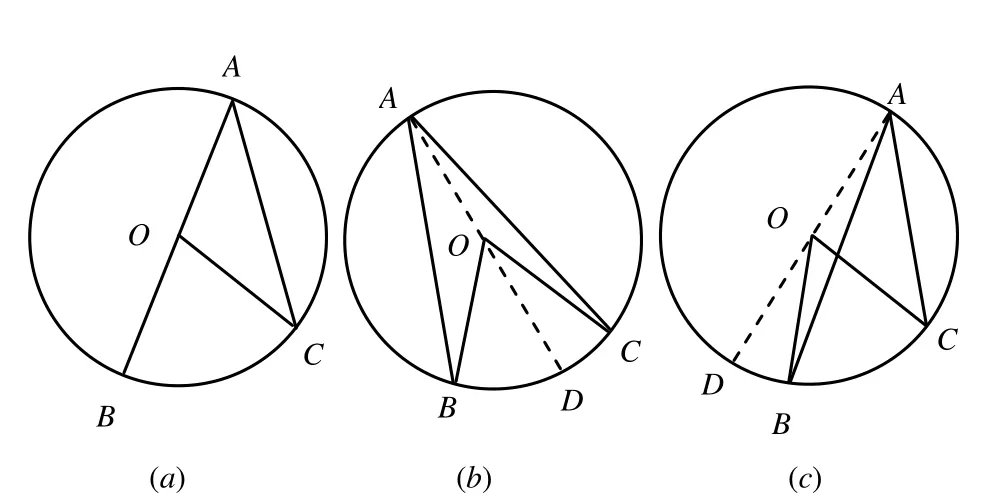
图1 圆周角定理
备课时,B老师通过问卷进行了学生调研,在回答“在与圆相关的计算和证明中常常需要添加辅助线,对于添加辅助线你有什么经验”的问题时,全班26名学生,有18名同学提到了“添加半径”.B老师分析道:学生的经验是添加半径、构造等腰三角形,但是这个定理的证明要添加直径(引自B老师的教学设计).
添加直径是教科书上的证明方法:
按照圆周角与圆心的关系分为3种情况(如图1所示).
在图1(a)中,∠BOC是等腰三角形AOC的顶角的外角,所以:∠BOC=2∠BAC.
图1(b)和图1(c)中,通过添加直径AD转化为图1(a)的情况即可.
课堂教学中,图1(a)和图1(b)的情况比较顺利,但是面对图 1(c)所示情况,学生普遍遇到了困难,不能完成添加直径转化为第一种情况的工作.此时,B老师做了引导,分析了图1(c)和图1(a)的关系,并连接了直径,然而,仍有许多学生处于困惑中,于是 B老师用彩色的粉笔,又仔细地描出对应的角,引导学生与图 1(a)进行比对,这时才有学生说“明白了”.
B老师在反思中写道:
在证明的过程中,大多数学生都走了偏路.
最困难的就是圆心在圆周角外的情况了,学生似乎毫无办法.即使有了前两种情况做铺垫,即使有的学生已经正确地添加了辅助线,但是仍然不能证出.于是我用彩色的粉笔,仔细地描出不同的角,原来这是一个作差的过程.有的学生恍然大悟了.定理虽然证完了,但是却没有时间进行定理的应用.
研究者在课堂中,观察到了这样一幕:生W面对第三种(图1(c))图形时,连接半径OA,于是问道:“为什么连接OA?”
W解释:这样就得到了等腰△OAC.
问:构造等腰三角形有什么用呢?
W:就有等角了.
问:那接下来呢?
W:还没想好.
接下来,由于 B老师开始集中讲解,该生没有再继续思考下去,但是该生在证明二倍角关系的时候能够联系起等腰三角形,这种思路是合理的,是不是也能够导致问题解决呢?研究者开始思考,得到了本题的另外一种证明方法.
因为△OAC是等腰三角形,∠DOC是顶角的外角,所以∠DOC=2∠OAC.
而题目要得到的结果是:∠BOC=2∠BAC,比较两式发现左边相差∠DOB,右边相差2∠OAB,而这恰好是由半径OA产生的等腰△OAB的顶角外角和底角,即∠DOB=2∠OAB,于是问题得以解决.
课后交流时,研究者将自己的观察与分析与 B以及在场的十几位老师交流时,大家也都感到惊诧:圆周角定理自己教了许多年,一直按照教科书的方式证明,也都知道添加直径是难点,但却没想过添加半径也能够证出,甚至是问题的本质,其实具体的证明方法真的不重要,真正的困难恰是学生不能从自己的已有经验和题目的具体特点出发,通过不断分析、调整、搭建题目条件与结论间的桥梁,直至解决问题的过程——从这个意义上看,B老师的教与学“擦肩而过”了.
3 对案例的分析
上面的案例中,教师 A的课堂出现的是教师从未遇到过的“意外”.导致这种意外发生的原因在于教师预先不知道学生面对最小公倍数这一特定问题会怎样思维,用 PCK理论解释就是:教师 A缺乏关于特定内容的教学知识,如果有了这种知识,A老师就能够更好地组织教学,避免教与学“擦肩而过”现象的发生.
显然,与A老师不同的是,B老师遇到的是自己预想之中的情形:对学生的调查和 B自己的经验都表明学生可能会添加半径做辅助线,做等腰三角形.也即 B具有关于圆周角定理这一特定内容学生是怎样思考的知识,但是,B却没有看到学生的方法的价值.原因在于 B认为“这个定理的证明要添加直径”,其潜台词就是“添加半径是解决不了问题的”.所以,B没有对学生的思维进行分析的原因不在于其缺乏的“学生是怎样思考的”知识,而是对圆周角定理的证明方法还有哪些,添加直径这种证明方法与学生经验中添加半径的方法的关系是怎样的缺乏思考和认识——这本质上是学科性知识,这种知识的缺失导致了 B的课堂中出现了教与学“擦肩而过”的现象.
实际上,如果进一步比较B老师课堂上生W的表现与A老师的课堂上生5的表现,可以发现两者之间具有很大的相似性.生5和生W在探究的过程中,首先发挥作用的是自身已有经验或者直觉——而这也是数学研究工作者面对问题时自然会产生的思维活动.如果再继续对经验或直觉进行批判性分析,也许就能够找到解决问题的路径,会发现自己的错误,而批判性分析在揭示了错误原因的同时,还可能成为新的发现源泉,就像前面对生5的方法的分析那样.
从这个意义上看,尽管表面上 A老师的课堂表现是由于出现了“意料之外”,在于不了解学生面对“最小公倍数”这一特定知识是如何思考的,但是根本原因在于 B老师的学科性知识的缺失.事实上,过于强调“特定内容的思考方式”是不利于问题解决的.数学知识浩如烟海,学生的思考方式更是五花八门,即使是同一个想法也可能会有不同的表现形式,即使有了几十年的教学经历仍然不能穷尽所有的情形.以学生的思考、探索为基础的课堂总会出现“意外”,因此,“特定内容的教学知识”不应该是影响其课堂决策的根本原因.从根本上看,解决 A老师问题的关键仍然在于发展数学学科性知识,不是扩充数学知识的数量,而是提高学科知识的质量,把重点放在提升教师对数学知识的产生过程的认识,帮助教师体会数学研究者面对问题的探究、思考方式的特点.
4 结论与讨论
在以学生的思考、探究为基础的数学课堂上,教师的教与学生的学出现“擦肩而过”现象的原因在于教师没能读懂学生的方法的潜在价值.要想解决这一问题,可以根据PCK理论,补充教师的关于特定内容的教学知识.按照这一策略,需要梳理中小学数学所有内容的教学知识,建立中(小)学数学PCK知识库,作为数学教师培训的内容之一——这是一项浩大的工程,目前也正成为中国学者关于PCK研究的热点.
但是,PCK理论中对“特定内容的教学知识”的强调存在着明显弊端.一方面,如上所述,依靠“穷尽各种可能”的方式面对充满活力和变数的学生探索过程是充满风险的.更为重要的是,强调“特定内容的教学知识”忽略了问题的本质,忽略了面对不同“特定内容”的探索和学习过程中的共性,忽略了教学中出现的问题的表层原因与根本原因的关系.这势必会导致张奠宙等批判的现象的出现:“数学教师培训的内容越来越泛化,只谈怎么教,无关教什么.”正如前面的分析,与特定内容的教学知识相比,教师的学科性知识的质量是导致课堂中出现教与学“擦肩而过”现象的更为根本的原因.因此,解决问题的根本途径应在于提高教师的数学学科知识水平,特别要重视数学学科性知识中的方法性知识.即,让老师们了解数学学科领域中知识的产生方式,数学研究者面对问题的探究、思考方式.
[1] 童莉.数学教师专业发展的新视角——数学教学内容知识(MPCK).数学教育学报,2010,19(4):23-27.
[2] 董涛.PCK研究回朔与对教师教育的意蕴——以数学学科为例[J].曲阜师范大学学报,2009,(4):121-124.
[3] 杨小丽.我国学者关于数学学科的PCK研究综述及对教师培训的启示[J].北京教育学院学报(自然科学版),2010,(6):48-52.
[4] 顿继安,张晓华.学科教学中漠视与低估学生的现象亟待关注[J].中小学管理,2008,(5):28-29.
[5] 李善良.我国高中数学课堂教学过程的演变与评析[J].数学通报,2010,(2):19-23.
[6] 张奠宙,赵小平.教什么永远比怎么教更重要[J].数学教学,2007,(10):封底.
- 数学教育学报的其它文章
- 培养儿童空间认知能力的有效途径探究——以拆拼孔明锁为例

