基于LSSVM的开关磁阻电机转子位置估算

徐宇柘 曹彦萍 钟 锐 屈 严 彭富林

(1东南大学国家专用集成电路系统工程技术研究中心,南京210096)

(2东南大学电子科学与工程学院,南京210096)

作为一种无需稀土材料的直流电机,开关磁阻电机(switched reluctance motor,SRM)具有结构简单、转矩大、成本低等特点,并在宽广的速度和功率范围内都能保持较高效率[1].近年来,随着稀土资源的日益减少,永磁无刷电机成本日益上升,SRM已逐渐引起电动车行业研究人员的重视.然而,位置传感器的引入不仅增加了电机结构的复杂性,又给安装、调试带来很大不便,严重削弱了SRM结构简单的优势.在恶劣环境下,位置传感器可能会脱落,造成安全隐患,降低了系统的可靠性[2].

为了增强SRM驱动系统的可靠性和鲁棒性,需要对无位置传感器控制技术进行研究[3].利用电机运行中电流、磁链等参数,估算出当前转子位置.然而,磁链在转子对齐位置的深饱和性使得SRM具有高非线性[4],增加了位置估算的复杂性.

位置估算的方法大致可分为主动法和被动法2种.主动法包括频率调制法和脉冲注入法.前者可用于位置估算[5],但是需要额外的脉冲发生电路;后者是指在电机的非导通相加入电压脉冲,与预设的电压值进行比较,估算出转子位置[6].但是,这2类典型的主动检测方法都需要对非导通相通入电流,影响电机运行.被动法包括观测器方法、模糊逻辑法、神经网络等.观测器方法的位置估算精度较高,但需要与磁饱和相关的复杂数学模型[7].模糊逻辑法的精度由规则的复杂度决定[8].神经网络具有较强的非线性映射能力,无需知道模型的先验知识,因而也常被用于位置估算[9];然而,神经网络所需样本大，存在局部极小点、过学习与欠学习等问题.支持向量机(SVM)[10]是以统计学习理论为基础的一种新型机器学习方法.它基于结构风险最小化原理,具有严格的数学依据,为解决小样本问题提供了很好的解决方案,并能有效避免上述神经网络的缺陷.文献[11]利用SVM建立转子位置预测模型,准确预测转子位置,实现了SRM的无位置传感器控制.最小二乘支持向量机(LSSVM)对SVM的损失函数和等式约束条件进行了修正,较之标准的SVM算法,简化了计算复杂性,提高了运算速度.文献[12-13]利用LSSVM分别建立了基于自感特性及矩角特性的SRM模型,并通过实测证明建模方法的正确性和有效性,避免了神经网络建模的固有缺陷,证明了LSSVM方法在回归预测方面的独特优势.

位置估算也属于回归预测.本文根据SRM磁特性数据,训练用于位置估算的LSSVM,并与改进的神经网络方法进行对比,分析其在精度及泛化能力上的优势.最后,搭建了一种基于LSSVM位置估算的SRM仿真模型,并将仿真结果和实测结果进行了对比.

1 LSSVM原理

SVM是建立在“结构风险”最小化理论基础上的,它将低维空间非线性样本经过核函数映射为高维空间中的线性样本,从而降低求解复杂性.LSSVM是支持向量机的一种改进,它将传统SVM中的不等式约束改为等式约束,且将误差平方和损失函数作为训练集的经验损失,从而把解二次规划问题转化为求解线性方程组问题,提高了求解问题的速度和收敛精度.

给定非线性系统的n个输入输出样本数据集(xi,yi),i=1,2,…,n,其中xi∈Rd,yi∈R,d为自变量维数.支持向量机利用此样本数据建立该系统的非线性模型.首先,通过一个非线性变换x→φ(x),将输入空间的样本点xi映射到一个高维的特征空间(Hilbert空间);然后,在该特征空间中进行线性建模,构造如下的最优决策函数:

f(x)=〈ω·φ(x)〉+b

(1)

式中,ω表示权重向量,且ω∈Rd;b表示阈值,且b∈R;〈·〉表示向量内积.

利用Vapnik结构风险最小化原则,可将寻找ω,b转化为对如下问题的优化:

(2)

s.t.yi=〈ω·φ(xi)〉+b+ξi

式中,ξi为松弛因子;c为正则化参数.

利用拉格朗日法求解这一优化问题,即

(3)

式中,αi≥0为拉格朗日乘子.

对式(3)求极值,令L对ω,b,ξi,αi分别取偏微分时值为0,解得

(4)

消去ω和ξ,得

(5)

式中

y={y1,y2,…,yn}
d={1,1,…,1}T
α={α1,α2,…,αn}T
Q=[φ(x1)Tφ(x2)T…φ(xn)T]T

采用最小二乘法求解式(5),求出α和b,得到基于核函数表示的非线性系统模型为

(6)

2 LSSVM位置估算

2.1 样本数据的获取

最小二乘支持向量机模型输入为电流i和磁链ψ,输出为角度θ,如图1所示.

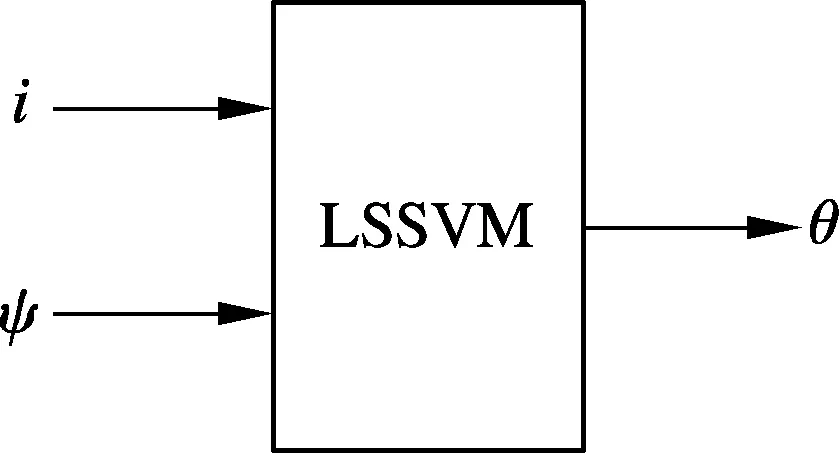
图1 基于LSSVM的位置估算

实验样机的参数设置如下:定转子结构为12/8极,额定功率为800 W,额定转速为3 600 r/min,额定转矩为2.1 N·m.

电机的磁链方程为

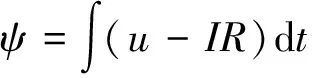
(7)

式中,u为相电压;I为相电流;R为绕组内阻.采用改进的DC脉冲法[14]得到不同角度下的相电压、相电流以及采样时间.由式(7)计算出磁链,并将ψ-I-θ磁链特性数据作为样本.

2.2 参数选择

核参数的选取对LSSVM预测的精度有很大影响.鉴于SRM的高度非线性及多变量耦合特点,本文选取非线性映射能力强、误差小的径向基(RBF)核函数,其基本形式为

(8)

式中,σ为宽度系数.

RBF核参数相对较少,更适用于SRM建模.该核函数需要确定校正因子γ和核宽度系数σ两个参数.本文中，将交叉验证法与凑试法相结合，选取最优参数对[11].

首先,采用交叉验证法寻优.选择训练点误差最小的2个参数值作为初始优化值,并统计参数的变化趋势对误差大小的影响.

然后,在确保训练点误差较小的前提下,分别以初始值为中心,根据总结的趋势适当缩放参数值,选取使训练点误差最小的一组参数值作为最终优化值.误差可分为以下2种形式:

1) 最大绝对误差.其定义式为

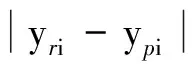
(9)

式中,yri为实测样本值;ypi为LSSVM预测的样本值.

2) 均方误差.其定义式为

(10)

最后,确定最优参数对为γ=35 000,σ=0.045.

2.3 LSSVM与神经网络位置估算比较

位置估算模块分别使用LSSVM和反向传播神经网络(BPNN)训练.图2为根据实验获取的样机磁链特性数据绘制的曲线.取其中676个数据作为训练样本,用于训练LSSVM和BPNN;将其余520个数据作为测试样本,用于验证精度和测试泛化能力.

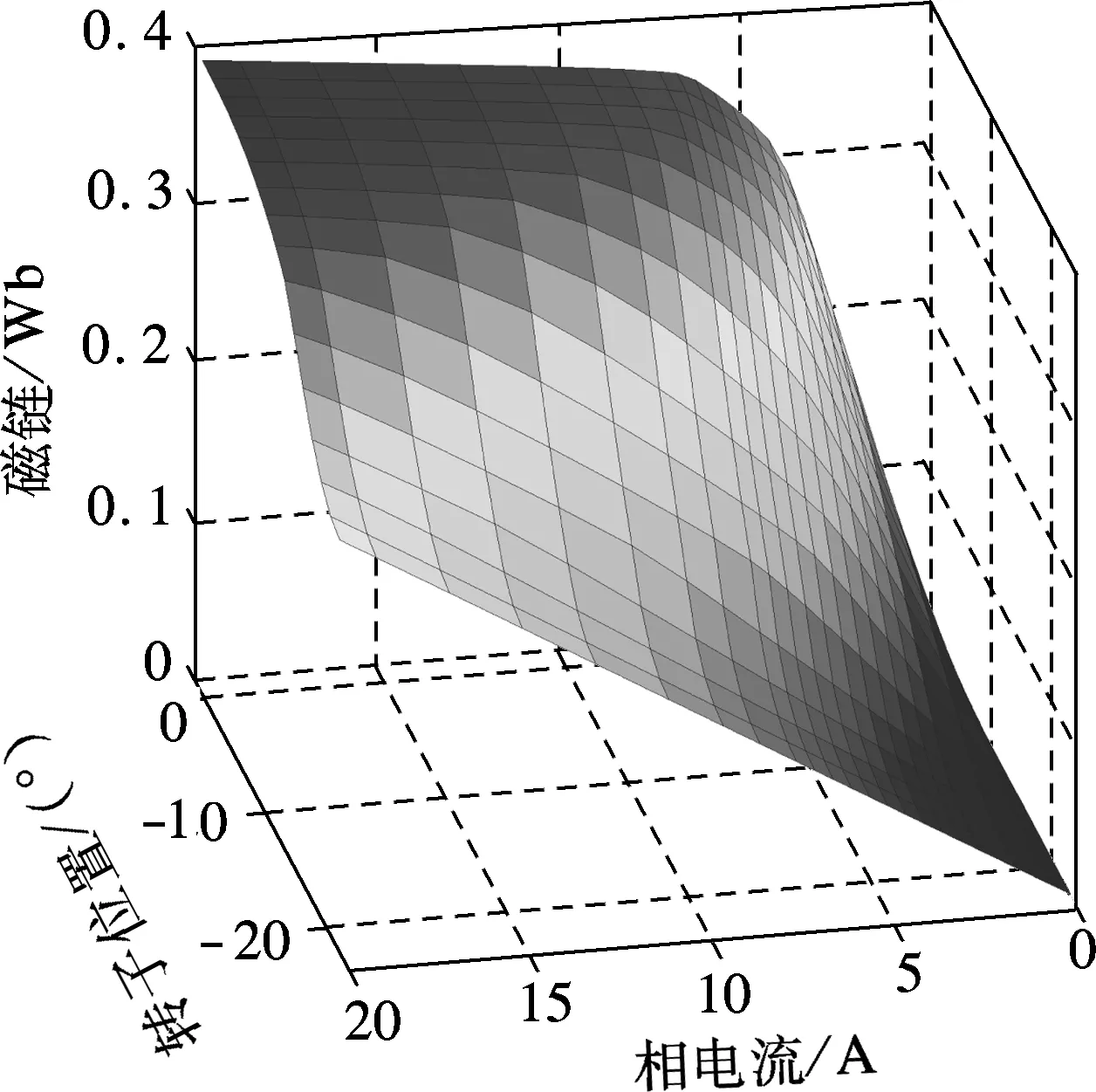
图2 样机磁特性数据曲线

神经网络采用改进的BPNN[15],此BPNN的运算速度较传统BPNN更快,同时保障精度不降低.经测试,神经元个数为15时效果最佳.利用训练样本对LSSVM和改进的BPNN进行训练,然后利用测试样本检验其泛化能力.对比结果见表1.由表可知,与改进的BPNN相比,LSSVM训练时间缩短了72%,训练样本的均方误差(MSE)减小了7.8%,测试样本的MSE减小了19.6%,即拥有更快的训练速度和较高的精度,且LSSVM测试样本的误差较训练样本减小64.5%,说明其泛化能力好,对未知数据的预测精度更高.

表1 LSSVM与改进BPNN的位置估算对比

3 仿真验证

为了验证本文建模方法的正确性,在Simulink软件中利用S函数建立SRM仿真系统(见图3).LSSVM位置估算模块输出转子位置的角度信息和速度,速度根据单位时间内转子经过的角度计算.SRM各相绕组交替开通,当一相电流为零时,无法对此相电流和磁链数据进行位置估算,可切换至相电流不为零的绕组,继续估算位置.SRM转动过程中总有一相电流不为零,最终可形成连续位置信号,输出范围为-22.5°～0°.为了方便比较,减少估算角度变换造成的误差影响,将仿真中实际角度输出设定在相同范围内.图4和图5中的实际值即表示仿真中转子位置,预测值表示LSSVM位置估算的值.

图3 LSSVM位置估算Simulink仿真系统图

图4 2 300 r/min时的转子位置预测值与仿真实际值

图5 800 r/min时的转子位置预测值与实测值

转速为2 300 r/min、负载为2.75 N·m时的角度波形与误差波形见图4.由图可知,LSSVM的最大转子位置预测误差为0.33°.

转速为800 r/min、负载为3.75 N·m时的角度波形与误差波形见图5.由图可知,LSSVM的最大转子位置预测误差为0.42°

初始转速为2 300 r/min时,负载由2.75 N·m突变到5 N·m,LSSVM位置估算模块输出的速度变化曲线和转子位置估算的误差曲线见图6.由图可知,速度变化期间,位置预测最大误差仅为0.6°,表明其具有良好的鲁棒性.

图4～图6所示的稳态和动态仿真结果表明,LSSVM的位置估算模块不仅能在不同转速下预测真实转子位置,还能在负载突变情况下准确预测速度变化趋势,位置预测的平均误差在0.1°以内.

需要指出的是,LSSVM对检测干扰敏感.实际应用中,磁链获取是对相电压的连续积分,为减少误差累积,应在每个相周期结束后复位磁链值归零.电流采样中,除硬件电路滤波外,应加入必要的软件滤波,推荐采用限幅滑动平均滤波,其优点是对脉冲性干扰抑制好,平滑度高,且延迟小.

图6 负载由2.75 N·m突变到5 N·m时的速度和位置预测误差

4 结语

本文利用LSSVM建立了SRM的转子位置估算模块,选择合适参数并训练了LSSVM.与改进的BPNN位置估算相比,LSSVM的训练时间缩短了72%,训练样本的均方误差减小了7.8%,测试样本的均方误差减小了19.6%,且泛化能力强.仿真验证结果表明，在稳态和动态情况下,LSSVM位置预测的平均误差在0.1°以内.LSSVM的位置估算模块能输出精确的转子位置信息,为精确的角度位置控制提供了基础,避免了位置传感器的固有缺点,简化了电机结构,提高了开关磁阻电机的可靠性.

)

[1]Soares F, Branco P J C. Simulation of a 6/4 switched reluctance motor based on Matlab/Simulink environment [J].IEEETransactionsonAerospaceandElectronic, 2001,37(3): 989-1009.

[2]Mese E, Torrey D A. An approach for sensorless position estimation for switched reluctance motors using artificial neural networks [J].IEEETransactiononPowerElectronics, 2002,17(1): 66-75.

[3]Fahimi B, Emadi A, Sepe R B. Four-quadrant position sensorless control in SRM drives over the entire speed range [J].IEEETransactionsonPowerElectronics, 2005,20(1): 154-163.

[4]Krishnan R.Switchedreluctancemotordrives:modeling,simulation,analysis,design,andapplications[M]. New York: CRC Press, 2001: 1-25.

[5]Ehssai M, Husaln I, Kulkami A B. Elimination of discrete position sensor sad current in switched reluctance motor drives [J].IEEETransactionsonIndustryApplications, 1992,28(1): 128-135.

[6]Afjei E, Cheshmehbaygi H M, Nouri H. Detecting the rotor position by employing pulse injection technique and digital pulse width modulation decoder in switched reluctance motor [C]//IEEEInternationalElectricMachines&DrivesConference. Antalya, Turkey, 2007: 40-44.

[7]Khalil A, Underwood S, Husain I, et al. Four-quadrant pulse injection and sliding-mode-observer-based sensorless operation of a switched reluctance machine over entire speed range including zero speed [J].IEEETransactionsonIndustryApplications, 2007,43(3): 714-723.

[8]Cheok A D, Wang Z. Fuzzy logic rotor position estimation based switched reluctance motor DSP drive with accuracy enhancement [J].IEEETransactionsonPowerElectronics, 2005,20(4): 908-921.

[9]Mese E. A rotor position estimator for switched reluctance motors using CMAC [J].EnergyConversionandManagement, 2003,44(4): 1229-1245.

[10]Cristianini Nello, Shawe-Taylor John. 支持向量机导论[M]. 李国正, 等译. 北京: 电子工业出版社, 2004.

[11]He Z, Xia C, Zhou Y, et al. Rotor position estimation for switched reluctance motor using support vector machine[C]//IEEEInternationalConferenceonControlandAutomation. Guangzhou, 2007: 1683-1687.

[12]Qu B, Song J, Jia H, et al. Nonlinear modeling of switched reluctance machine [C]//InternationalConferenceonElectricalMachinesandSystems(ICEMS). Beijing, China, 2011:1-4.

[13]宋建成,郑建斌,曲兵妮,等.开关磁阻电机的最小二乘支持向量机建模与仿真[J].电机与控制学报, 2010, 14(5): 32-36.

Song Jiancheng, Zheng Jianbin, Qu Bingni, et al. Modeling and simulation for switched reluctance motor based on least squares support vector machine [J].ElectricMachineandControl, 2010,14(5): 32-36. (in Chinese)

[14]Carstensen C E, Fuengwarodsakul N H, de Doncker R W. Flux linkage determination for correct modeling of switched reluctance machines-dynamic measurement versus static computation [C]//IEEEInternationalElectricMachines&DrivesConference. Antalya, Turkey, 2007: 1317-1323.

[15]Zhong R, Wang Y B, Xu Y Z. Position sensorless control of switched reluctance motors based on improved neural network [J].IETElectricPowerApplications, 2012,6(2): 111-121.