基于量子云模型演化的最小属性约简增强算法
丁卫平 王建东 管致锦 施 佺
(1南京航空航天大学计算机科学与技术学院,南京210016)
(2南通大学计算机科学与技术学院,南通226019)
(3南京大学计算机软件新技术国家重点实验室,南京210093)
属性约简是粗糙集理论[1]中一个重要的研究内容,其主要任务是在保证知识库分类和决策能力不变的条件下, 删除不相关或不重要的属性.现有大部分属性约简研究工作主要是采用基于代数表示与信息表示的相关方法[2-3],由于Wong[4]等已证明求决策表的最小属性约简是一个NP-hard问题,因此要设计一种通用且高效的最小属性约简算法相当困难.进化算法作为一类有效的全局优化技术,通过模拟或揭示某些自然现象或过程而得到迅速发展,在解决NP-hard问题上显示出较强的优势.近年来,一些学者为了改善传统属性约简方法的不足,相继开展了一些基于生物进化算法的启发式属性约简方法的研究,如Slezak等[5]提出了基于遗传算法序列的近似熵属性约简算法;Jensen等[6]提出了基于蚁群优化算法的粗糙属性约简方法;Ye等[7]提出了基于二进制粒子群优化的最小属性约简算法.上述属性约简算法能充分利用进化算法搜索最优解的优势,较好地进行最小属性约简中最优值的演化求解,然而这些属性约简算法往往也无法避免一般进化算法易出现的早熟收敛和进化停滞等问题,在求最小属性约简集时效率和精度大大降低.
云模型是一种定性知识描述和定性概念与其定量数值表示间的不确定性转换模型,主要反映客观世界事物或人类知识中概念的模糊性、随机性,并把两者完全集成在一起[8].云模型理论的随机性可避免搜索陷入局部极值,而其稳定倾向性又可很好地定位全局最优值.近年来,融合云模型和进化计算的云进化算法引起了国内外学者的关注.如戴朝华等[9]利用云发生器代替传统遗传算法中的交叉、变异算子, 提出了一种全新的云遗传算法;刘禹等[10]利用云模型的超熵变化控制进化策略来模拟进化选择压力和控制进化基因频率,提出了基于云模型雾化特性的进化算法;张光卫等[11]采用云模型对物种遗传变异进行统一建模,提出了基于云模型的进化算法.上述研究表明采用云模型对进化算法进行优化,可使其在定性知识的指导下能自适应控制搜索空间范围,具有快速的收敛速度和较强的全局搜索能力.
量子进化算法具有独特的相干性、叠加性和并行性等,能快速提高进化算法寻求最优解的速度,近年来受到众多学者的高度关注[12].本文将云模型理论和量子进化算法进行融合并引入到粗糙集最小属性约简领域,提出了一种基于量子云模型演化的最小属性约简增强算法(QCMEARE).该算法能更好地发挥云模型和量子进化算法在最小属性演化约简过程中的全局寻优性能和最小约简求解效率,实验结果表明其最小属性约简是高效和实用的.
1 属性约简概念与模型

定义2在决策表S=(U,C∪D,V,f)中,对于∀B∈C,存在POSB(D)=POSC(D),且若∀ci∈B,POSB-{ci}(D)≠POSC(D),则称B为C相对于D基于正区域的属性约简.
定义3在决策表S=(U,C∪D,V,f)中,C相对于D所有基于正区域的属性约简集为PR(C),Core(C)=∩PR(C)为基于正区域的核.

定义5属性演化约简模型是将进化种群个体编码成“0-1”组合形式,设条件属性C的势Card(C)=N,则其编码表示为X={x1,x2,…,xN}∈{0,1}N,其中“1”表示对应属性被选中,“0”表示对应属性未被选中.

s.t.
x∈{0,1}N,γξ(x)=γC, Core(ξ(x))=ξ(x)
上述优化目标模型可利用二进制优化算法进一步求解,设一个确定的布尔向量X={x1,x2,…,xN}∈{0,1}N代表一个种群个体,xi(i=1,2,…,N)表示种群中标号为i的个体,N为进化种群中个体总数.
2 基于约简属性熵权的逆向云生成算法
云模型[8]所表达概念的整体特性可用云的3个数字特征来反映,即期望Ex、熵En和超熵He,记作(Ex,En,He).逆向云算法是云模型中的一个关键算法,它是将一定数量的精确数据有效转换为以恰当定性语言值(Ex,En,He)表示的概念,其输入为n个云滴在数域空间的精确位置和每个云滴代表该概念的确定度,输出则为这n个云滴表示定性概念的期望值Ex、熵En和超熵He.
下面根据属性约简过程各条件属性熵权大小给出相应逆向云生成算法,主要步骤如下:
① 根据属性决策表S=(U,C∪D,V,f)构建一个判断矩阵R,即R=(ri,j)n×m(i=1,2,…,n;j=1,2,…,m),其中m为条件属性C的个数,n为决策属性D的个数.

③ 将m个条件属性和n个决策属性所确定的属性熵值定义为

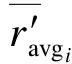
④ 计算第i个条件属性的熵权为
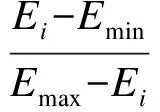
式中,Emax,Emin为条件属性熵值中的最大值和最小值,则决策表条件属性熵权集W={w1,w2,…,wn}.
⑤ 输入n个云滴集合X={x1,x2,…,xn}和条件属性熵权值集合W={w1,w2,…,wn},将各条件属性确定的属性熵权视作为每个云滴代表该属性的确定度.
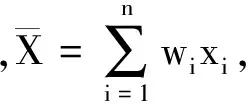
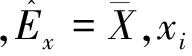
3 基于云模型的量子进化算子
3.1 量子基因云编码

在量子进化算法中, 使用一对复数(α,β)定义一个量子比特位.一个具有k个量子比特位的种群可用长度为k的量子染色体(2k个态)形式描述如下:

一个量子染色体可表征为解空间中任意解的叠加态,在此采用基于约简属性熵权的逆向云生成算法完成数值空间到概念空间的转换,用云模型模拟一个进化种群中所有量子个体同一个基因的分布特征,并定义其为该种群的一个基因云.基因云是一个种群中个体基因值的定性表示,反映了种群基因的整体统计特征,量子进化种群第i个基因的基因云可记为(Exi,Eni,Hei).这样进化过程中可利用定性进化策略对种群进化操作进行定性控制,即通过调整种群基因云参数(Exi,Eni,Hei)来优化子代种群的产生,并对染色体编码,使种群多样化,防止其陷入局部最优.通过上述策略使进化种群在基因云定性知识指导下自适应控制属性约简空间搜索范围.
3.2 量子云旋转门
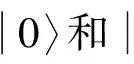

根据约简属性熵权逆向云算法生成的(Exi,Eni,Hei),本文提出了一种自适应的量子云旋转角调整方法.在进化初期,旋转角θi根据逆向云生成的(Exi,Eni,Hei),将进化个体适应度f(x)i与当前迭代中最优适应度f(b)i、全局最优适应度f(B)进行比较,自适应确定旋转角,从而迅速完成全局搜索,使当前迭代中的最优解不断趋近于全局最优解.随着种群进化代数增加,旋转角θi呈指数减小,从而种群转向局部的精细化搜索.量子旋转角计算公式定义如下:
式中,Δθi表示量子种群染色体中第i个量子比特与基态间的角距离,其定义为
式中,i表示当前进化代数;Imax表示最大进化代数. Δθi的取值将保证量子种群染色体中所有量子比特都朝着与最优解对应的量子比特基态进行偏转,使进化种群在定性知识指导下能够自适应精细地搜索属性空间范围.
该量子旋转角θi将进化种群个体适应度f(x)与当前迭代中最优适应度f(b)i、全局最优适应度f(B),分别与云模型的(Exi,Eni,Hei) 3个特征进行有效结合,可更加自适应地调整量子旋转角及其旋转门,使进化种群在云模型定性知识指导下自适应调整属性空间搜索范围,有效地平衡全局搜索与局部搜索之间的矛盾,最终使得进化种群稳定而高效地收敛于全局最优值.
3.3 量子云变异
量子进化过程的变异操作可提升算法摆脱局部极值的性能,加速其全局收敛.本文采用基于约简属性熵权的逆向云模型设计动态变异概率,增强量子种群跳出局部极值的能力,以保证进化的方向性和种群的多样性.量子云变异操作随着种群进化,其个体退化程度将降低,变异概率将逐渐减小,以更好地保持前期所探索的解.

式中,0.05 量子云变异概率Pm的确定同时考虑了进化种群的3个极值(f(x)i,f(b)i和f(B))和逆向云模型定性表示(Exi,Eni,Hei)的值,通过量子云变异操作更改相应量子比特态叠加状态,使量子进化算法稳定而高效地收敛到全局最优解. 量子进化种群在量子云变异Pm后,结合逆向云的3个特征(Exi,Eni,Hei)和量子云旋转角θi对操作进行量子纠缠,第i个量子位上任意2个量子比特a,b的量子云纠缠算子定义为 量子进化种群采用上述量子云纠缠可较好地进行非定域量子门的定性操作,极大地提高其纠缠的成功几率,使进化种群在定性知识指导下能够自适应快速进化. 基于上述设计的量子云模型演化算子,根据粗糙集中最小属性约简模型,本文提出了一种基于量子云模型演化的最小属性约简增强算法(QCMEARE),其核心思想为:首先将属性约简集映射至进化种群空间,然后基于约简属性熵权生成的逆向云模型,在逆向云模型3个特征(Exi,Eni,Hei)的定性指导下进行量子种群基因云编码,并结合种群精英量子个体进行量子旋转角自适应调整、量子云变异和量子云纠缠操作,使进化种群在定性知识指导下自适应控制约简属性空间搜索范围,较好地搜索到全局最优解.该QCMEARE算法能够在粗糙属性约简过程中尽可能地减少所包含的属性数目,充分发挥云模型和量子进化算法在最小属性演化约简过程中的全局寻优性能,获得较理想的最小属性约简集.该算法核心步骤流程如图1所示. 图1 QCMEARE算法核心步骤流程 为验证QCMEARE算法在属性约简优化方面的性能,本文进行了基于典型UCI机器学习数据库[13]属性演化约简性能比较实验.实验平台为:Microsoft Windows 2003 Server,MSSQL Server 2005,Visual Studio 2008 C#.NET开发工具,Intel双核CPU 1.66 GHz,1 GB内存,120 GB硬盘.对比算法选取2种典型的快速属性约简算法:BPSOAR算法[7]和 PS-FS算法[14].以5倍的原数据代替其相应数据集进行大规模数据量扩展决策表测试,在每个扩展数据集上进行20次交叉验证,实验结果为去除最初1次和最后1次,中间18次实验结果的平均值.图2给出了其中5个UCI数据集取得最小属性约简集时平均约简精度和约简时间值.从图中可看出,QCMEARE算法在5个UCI数据集上均取得了较好的约简性能,其约简精度普遍高于其他2种算法,尤其在Exactly和Mushroom数据集上平均约简时间明显低于其他2种算法,如在Mushroom数据集上,QCMEARE算法的属性约简平均时间为2.4 s, 而其他2种算法为4.0和6.1 s.这表明QCMEARE算法在属性约简过程中较好地解决了一般基于进化的属性算法所面临的精度与效率冲突问题,从而获得了较为满意的属性约简效果, 提高了其实际可用性. 图2 不同算法在UCI数据集上属性演化约简性能比较 图3(a)、(b)是QCMEARE算法与BPSOAR, PS-FS算法在大规模Vehicle, Postoperative数据集上随着属性约简器数量增加其属性约简精度稳定性比较分析.从图中可看出,QCMEARE算法在属性约简器数量动态增加时,约简精度基本呈上升趋势且精度值较高,逐步达到平稳状态,这表明QCMEARE算法在粗糙属性约简时具有较好的稳定性. 图3 QCMEARE算法属性约简精度稳定性分析 云模型克服了模糊数学用精确、唯一的隶属函数严格表示模糊概念的缺点,在定性与定量之间相互转换时具有较好的特性.量子进化算法具有独特的量子相干性、变异性和纠缠性,能快速提高进化种群全局最优解的搜索能力.本文融合两者优势提出了一种基于量子云模型演化的最小属性约简增强算法QCMEARE.相关实验结果及其分析表明,本文提出的QCMEARE算法是可行的和高效的,其属性约简效率和精度较其他算法具有明显的增强优势.接下来将更深入地研究量子云进化算法的自适应性及其理论基础,以进一步增强属性演化约简算法的性能. ) [1]Pawlak Z. Rough sets[J].InternationalJournalofComputerandInformationSciences, 1982,11(5): 341-356. [2]Wang G Y. Rough reduction in algebra view and information view[J].InternationalJournalofIntelligentSystems, 2003,18(6): 679-688. [3]Yao Yiyu, Zhao Yan. Attribute reduction in decision-theoretic rough set models [J].InformationSciences, 2008,178(17): 3356-3373. [4]Wong S K M, Ziarko W. On optimal decision rules in decision tables[J].BulletinofPolishAcademyofScience, 1985,33(11): 693-696. [5]Slezak D, Wroblewski J. Order based genetic algorithms for the search of approximate entropy reducts[C]//ProceedingsofRSFDGrC’2003. Chongqing, China, 2003: 308-311. [6]Jensen R, Shen Q. Finding rough set reducts with ant colony optimization [C]//Proceedingsofthe2003U.K.WorkshoponComputationalIntelligence. Bristol, UK, 2003:15-22. [7]Ye Dongyi, Chen Zhaojiong, Liao Jiankun. A new algorithm for minimum attribute reduction based on binary particle population optimization with vaccination[C]//Proceedingsofthe11thPacific-AsiaConferenceonAdvancesinKnowledgeDiscoveryandDataMining. Nanjing, China, 2007: 1029-1036. [8]李德毅, 刘常昱. 论正态云模型的普适性[J].中国工程科学, 2004, 6(8):28-33. Li Deyi, Liu Changyu. Study on the universality of the normal cloud model[J].EngineerandScienceofChina, 2004,6(8): 28-33. (in Chinese) [9]戴朝华, 朱云芳, 陈维荣,等. 云遗传算法及其应用[J]. 电子学报, 2007,35(7):1419-1424. Dai Chaohua, Zhu Yunfang, Chen Weirong, et al. Cloud model based genetic algorithm and its applications[J].ActaElectronicaSinica, 2007,35(7): 1419-1424. (in Chinese) [10]刘禹,李德毅,张光卫,等. 云模型雾化特性及在进化算法中的应用[J]. 电子学报, 2009, 37 (8):1651-1658. Liu Yu, Li Deyi,Zhang Guangwei, et al. Atomized feature in cloud based evolutionary algorithm[J].ActaElectronicaSinica, 2009,37(8):1651-1658. (in Chinese) [11]张光卫,何锐,刘禹,等. 基于云模型的进化算法[J]. 计算机学报,2008,31(7):1082-1091. Zhang Guangwei, He Rui, Liu Yu, et al. An evolutionary algorithm based on cloud model[J].ChineseJournalofComputers,2008,31(7):1082-1091. (in Chinese) [12]Zhang G X. Quantum-inspired evolutionary algorithms: a survey and empirical study[J].JHeuristics, 2011,17(3): 303-335. [13]Asuncion A, Newman D J. UCI repository of machine learning databases [EB/OL]. (2007-06) [2012-09-20]. http://www.ics. uci.edu/~mlearn/mlrepository. [14]Chen Yumin, Miao Duoqian, Wang Ruizhi, et al. A rough set approach to feature selection based on power set tree[J].Knowledge-BasedSystems, 2011,24(2): 275-281.3.4 量子云纠缠
4 基于量子云模型演化的最小属性约简增强算法

5 仿真实验与结果分析


6 结语

