基于压缩感知的云存储系统状态监测方法
冯 径 张梁梁 沈 晔 梁陆萍
(1解放军理工大学气象海洋学院气象水文指挥系, 南京 211101)
(2解放军理工大学第六十三研究所,南京 210007)
异常状态的及时监测对提升云存储效率有重要意义.为了对大规模云计算平台的异常状态进行有效监测, Kung等[1]将压缩感知理论应用于云计算状态监测中.压缩感知理论是应用数学和信号处理领域中的一个新的研究方向,这一理论对于稀疏性信息的处理具有明显优势[2-3].压缩感知理论指出,对于可压缩的信号,利用远低于奈奎斯特准则的方式进行数据采样后,仍能精确地恢复出原始信号.
在常规状态监测中,通常利用主控服务器对注册到云存储平台的所有存储服务器进行轮询,或者由各存储服务器周期性地向主控服务器发送心跳信息[4].这2种方法仅适用于云存储系统规模较小的情况.随着云存储系统规模的进一步扩大,前一种方法会带来较大的延时,导致监测结点收集到的状态不能及时反映全局当前状态;后一种方法则会在心跳报文向上汇总时出现数据量膨胀的现象,对主控服务器产生类似于“洪泛攻击”的影响,针对这一问题,目前工程上的解决办法是降低心跳频率,但这会导致监测精度降低[5].
本文对经典压缩感知理论进行了改进,设计了一种适用于FFS云存储异常状态监测的方法,并构造了一种适合于测量云存储系统状态的行和为零的贝努利测量矩阵.利用改进后的压缩感知方法对FFS集群监控机制进行调整,并在仿真环境下对解码精度、压缩比率、定位效率进行测试和分析.
1 压缩感知理论及其算法改进
1.1 压缩感知理论
压缩感知理论[2-3]是一种关于在欠采样条件下重构原始信号的理论,即已知原始信号X和测量矩阵Φ(Φ∈RM×N,M≪N),将X投影到Φ,则线性测量值为
Y=ΦXY∈RM
(1)
显然,由于Y的维数远低于X的维数,方程(1)有无穷多个解,即这是一个不适定问题.然而,如果已知所寻找的解为这无穷多个解中最稀疏的,且Y与Φ满足约束等距性条件(RIP)[6],则信号X可以由测量值Y通过求解最小l0范数来精确重构,即

(2)
然而,常见的自然信号S在时域内几乎是不稀疏,故上述信号的重构过程不能直接用于自然信号重构,需要通过某正交变换Ψ将自然信号S进行稀疏表示,即X=ΨS.
由此可知,压缩感知理论包含3个方面:测量矩阵的设计、稀疏信号的重构以及自然信号的稀疏表示.由于云计算平台的异常状态信息具有稀疏性,因此本文仅关注前2个方面.
目前,已有不少类型的测量矩阵被相继提出,最常用的包括高斯随机测量矩阵和贝努利随机测量矩阵等[7].这类测量矩阵具有强的随机性,文献[8]已从理论上证明其满足RIP性质.高斯随机测量矩阵可表示为
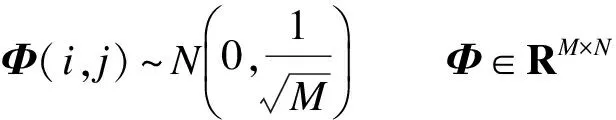
(3)
贝努利随机测量矩阵可表示为
(4)
利用式(2)可以完成信号的重构,但Donoho等[2]指出,求解最小l0范数是NP问题,无法直接求解.为此,研究者们提出了一系列求次优解的算法,如匹配追踪(matching pursuit, MP)算法[9]及其改进算法等.MP算法的本质是贪婪迭代算法,具体过程见算法1.
算法1MP算法

② 找到索引λt,使得
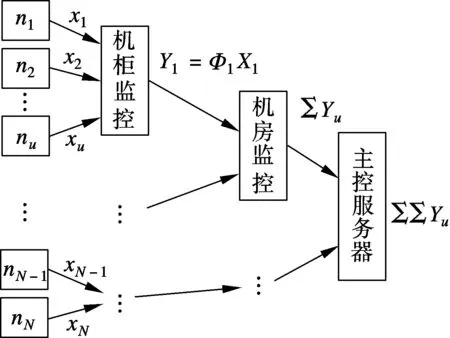
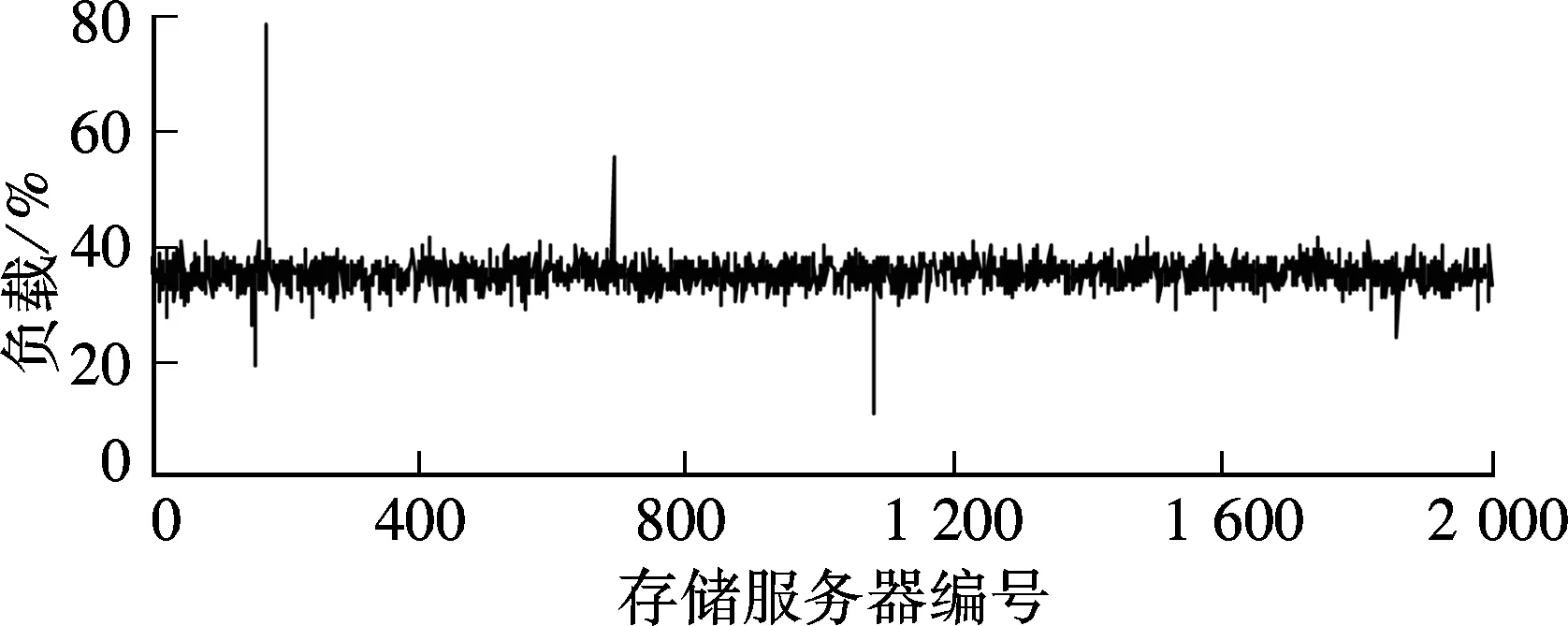
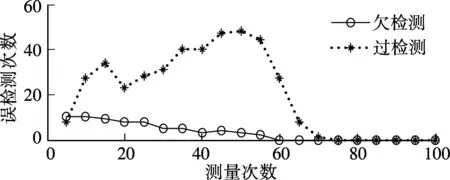
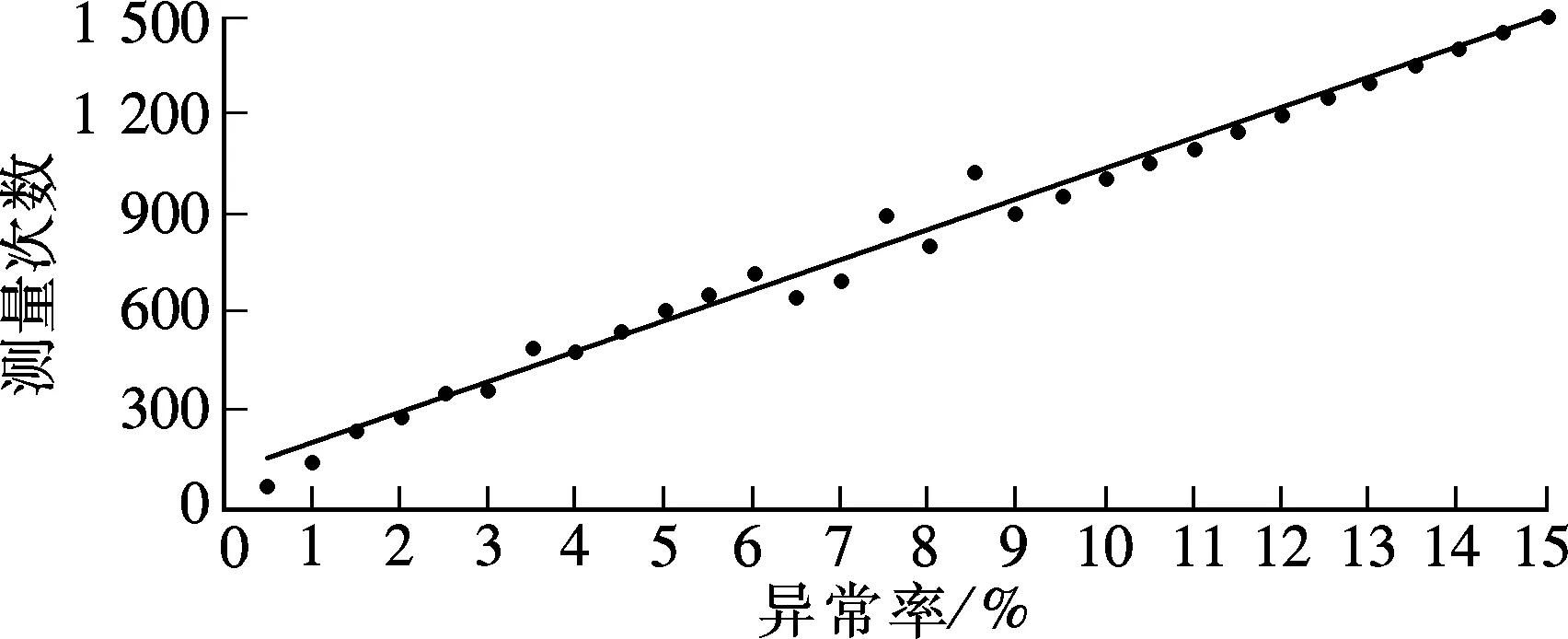
④ 令t=t+1,如果t 文献[9]对MP算法的收敛性进行了理论推导.本文针对FFS云存储系统异常状态监测的实际需求,对经典压缩感知理论中的重构目标函数进行改进,并证明在特定测量矩阵的条件下,改进后的目标函数与原有目标函数等价,即MP算法依然适用. FFS云存储系统异常状态监测中采集的信号包括磁盘占用率、网卡负载、网络延迟等.在同构的云存储集群中,这类信号通常包含某一直流分量,故不属于经典稀疏信号. 针对包含直流分量的稀疏信号,需要对经典压缩感知理论中的目标函数进行修改,即 (5) 为了使式(5)与式(2)等价,需要选择满足行和为零的测量矩阵,即 (6) 由此可知,ΦC=0,式(5)等价为 (7) 式中,Δ=X-C. 下文中出现的测量矩阵,若无特别说明,均指通过这种方法构造的行和为零的贝努利矩阵. 主控服务器通过轮询的方式收集各存储服务器的负载.随着存储集群的增大,轮询周期增加,监测精度降低.本文采用基于压缩感知的异常状态测量方法SDCS (state detection with compressive sensing)对FFS原先状态收集机制进行改进. FFS是通用低性能PC集群构建的高可靠高性能云存储系统,由三大模块组成:主控服务器模块、存储服务器模块和客户端代理模块[10].系统结构如图1所示.这种系统结构包含2个主控服务器,采用主-备的工作方式(Active-Standby),即一台服务器处于某种业务的激活状态(Active状态),而另一台服务器处于该业务的备用状态(Standby状态). FFS中异常状态是指存在少部分存储结点,由于新加入或者发生故障的原因,导致其磁盘耗费偏离平均值.当多个热点文件被存储于同一台存储服务器时,该服务器的网卡占用率明显高于其他存储服务器.对于大规模的云存储系统,这类异常状态往往只发生于少数结点上,具有稀疏性,故可采用压缩感知方法监测. 图1 FFS云存储系统部署图 云存储集群在长期运行后会出现数据分布不平衡的问题.为新建文件分配存储服务器时,不仅需要考虑磁盘负载,还要考虑存储服务器的工作负载,它们之间存在乘性关系.存储服务器的负载值计算公式为 (8) 式中,xw为存储集群中第w台存储服务器的负载值,%;aw为存储服务器的磁盘可用空间百分数,%;uw,dw,nw分别为存储服务器网卡的上行速率、下行速率和最大速率,kbit/s.主控服务器会根据各结点的负载值周期性地对存储服务器列表进行排序. 异常程度可表示为 对于大规模FFS云存储系统,需采用分层状态测量机制(见图2). 图2 分层状态测量的拓扑结构 由图2可知,根据式(8),机柜监测结点收集本机柜内各存储服务器的负载信息,并生成新的测量值Yi=ΦiXi.机房监控结点用于收集其所属各机柜监控结点的测量值,并将这些测量值累加生成新的测量值.最终,将各机柜测量值的累加值汇总至主控服务器,即 Y=∑ΦcXc=ΦX (9) 式中,c为机柜总数. 这种测量机制的优点在于:① 状态测量中,中间结点与主控服务器仅需执行简单的累加操作.与传统墒编码方式相比,这种编码方式的复杂度较低.② 状态信息从底层向主控服务器汇总的过程中,数据维度保持不变,避免了数据量膨胀问题.③ 中间结点总是保存其下层结点的最后一次状态测量值.这种方式无需对全局数据进行同步,且不依赖于数据的可靠传输. 主控服务器对收集到的状态测量值进行周期性重构,即求解式(9)的稀疏解.对于状态向量X,偏离均值较大的分量往往对应异常程度较严重的状态参数.因此,利用MP算法,可优先定位到异常程度较严重的结点上,从而使主控服务器可以按异常严重程度发现感兴趣的结点,并及时进行处理. 在FFS中,实时获取全局状态信息有利于任务分配和资源调度的优化.如多个热点数据存放在同一台存储服务器上,该存储服务器将成为瓶颈结点,实时获取云存储平台全局状态有利于及时将瓶颈结点的热点数据进行重分配,从而提高云存储系统的吞吐量(MBPS)和响应速度(IOPS)[11]. FFS中主控服务器模块对云存储客户端提供目录服务和元数据服务,并对存储服务器集群进行监控,部署于一台性能较好的服务器中.下面针对FFS中的服务器进行监测仿真,其拓扑结构见图1. 采用Matlab软件进行仿真.假设FFS云存储系统中包含2000个存储服务器、1个主控服务器和1个备份服务器.如图3所示,大部分存储服务器的负载值约为35%.仅少部分存储服务器(10个,占总数的0.5%)的负载远偏离于平均水平,这类存储服务器存在某种异常,可能是新加入的结点,也可能存在热点数据,或者发生软硬件故障,需要通过状态监测及时发现,并进行数据迁移. 图3 各工作结点子任务完成进度 利用基于压缩感知的监测方法,选取不同的测量次数,分别对图4所示的状态信息进行了测量和重构,并将重构结果与原状态分布情况进行比较. 图4 不同测量次数下的重构误差曲线 重构误差分为2种:① 过检测,即将某非异常结点误判为异常结点;② 欠监测,即未能检测出某异常结点.这2种误差中,过检测可通过系统的二次确认进行修正,但会在一定程度上增加系统的二次确认开销;欠检测可在系统的后续重构周期得到修正,但会降低系统探测到异常结点的效率. 图4为不同测量次数下的重构误差曲线. 由图4可知,对于稀疏度为10的原状态信息,当测量次数超过70时,即可无误差地精确定位所有异常结点.此时,数据的压缩比率达到3.5%.即在保持与常规状态监测方法相同的监测精度下,若集群中异常结点数占总结点数的0.5%,则基于压缩感知的监测方式所能有效监测的集群规模比常规方式提高约28.6倍. 为了测试SDCS在集群异常率不同时的压缩比率,将异常率(即集群中异常结点数占总结点数的百分数)控制在0.5%~15%,对SDCS选取不同的测量次数分别进行了实验,结果见图5. 图5 测量次数与异常率的关系 对所测得的数据进行线性拟合,得到拟合后的线性方程为 f(ε)=9274ε+101.2 (10) 式中,ε表示异常率;f(ε)表示测量次数.令γ(ε)=f(ε)/2000为本文方法相对于轮询与心跳监测方法所占用网络监控流量的压缩比率,则 (11) 由此可知,当集群中异常率低于20.5%时(绝大多数可正常工作的网络都满足该要求),相对于传统方法,使用本文方法可更有效地压缩监控流量. 本实验验证了在重构原始状态信息的迭代过程中,定位异常结点的先后顺序与结点异常程度间的关系.仿真条件与3.2节相同,测量次数为80,统计结果见图6. 图6 定位顺序与结点异常程度的关系 如图6所示,重构算法共迭代了10次,按迭代顺序所定位的结点,其异常程度的绝对值依次下降,说明该算法具有优先定位当前异常程度最严重结点的优良特性.通过异常状态的成功检测,可以在FFS中采用负载均衡机制来保证各存储结点的磁盘耗费与网卡占用率接近平均值. 本文对压缩感知理论进行了改进,提出了一种SDCS方法,并将其应用于解决大规模FFS云存储系统实时监测问题中,证明了采集综合状态信息的可行性与有效性,分析了有效压缩监控流量的集群异常率阈值.与传统状态监测方法相比,SDCS方法编解码复杂度低,监测精度高.测量数据从底层向主控服务器汇总过程中,数据维度可保持不变,便于采集含有多种要素信息的信号,避免了常规监测方法在监测大规模云存储平台时出现的数据膨胀问题,使得监测规模可进一步提高.在数据重构过程中,优先定位当前异常程度较严重的结点,可有效提高系统异常恢复效率.在下一步工作中,将研究如何针对具体情况对各类状态进行统一编码. ) [1]Kung H T, Lin C K, Vlah D. CloudSense: continuous fine-grain cloud monitoring with compressive sensing[C]//Proceedingsofthe3rdUSENIXWorkshoponHotTopicsinCloudComputing. Portland, OR, USA, 2011:15-19. [2]Donoho D L. Compressed sensing[J].IEEETransactionsonInformationTheory, 2006,52(4): 1289-1306. [3]Candes E J. Compressive sampling[C]//ProceedingsoftheInternationalCongressofMathematicians. Madrid, Spain, 2006(3): 1433-1452. [4]Lei L, Wo T Y, Hu C M. CREST: towards fast speculation of straggler tasks in MapReduce[C]//ProceedingsoftheIEEE8thInternationalConferenceonE-businessEngineering. Beijing, China, 2011: 311-316. [5]Tom White.Hadoop:thedefinitiveguide[M]. Sebastopol, CA, USA:O’Relly Media Inc, 2011: 170-173. [6]Candes E J. The restricted isometry property and its implications for compressed sensing[J].ComputesRendusMathematique, 2008,346(9/10): 589-592. [7]Tsaig Y, Donoho D L. Extensions of compressed sensing[J].SignalProcessing, 2006,86(3): 549-571. [8]Baraniuk R, Davenport M, Devore R, et al. A simple proof of the restricted isometry property for random matrices[J].ConstructiveApproximation, 2008,28(3): 253-263. [9]Davis G, Mallat S, Avellaneda M. Adaptive greedy approximations[J].ConstructiveApproximation, 1997,13(1): 57-98. [10]Wu Haijia,Chen Weiwei,Hu Guyu. FFS: a PB-level cloud-storage system based on network [J].JournalonCommunications, 2011,32(9): 24-33. [11]Wu Haijia,Chen Weiwei, Liu Peng. Synchronization strategy for metadata cache in cloud storage system based on change-log[J].TelecommunicationsScience,2011,27(9): 32-36.1.2 含直流分量的稀疏信号压缩感知方法





2 基于压缩感知的状态监测方法
2.1 FFS

2.2 FFS异常状态

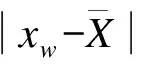

2.3 异常状态测量机制

3 仿真
3.1 仿真背景
3.2 仿真环境
3.3 解码精度
3.4 压缩比率测试

3.5 定位效率测试

4 结语

