基于最近离散点的光线跟踪

蔡 鹏， 尹宝才， 孔德慧

（北京工业大学计算机学院多媒体与智能软件技术北京市重点实验室，北京 100124）

基于点云模型的光线跟踪算法得到很多的关注，因为它在全局光照方面提供了高质量的绘制效果。目前，点云模型的光线跟踪算法的点元，除了包含三维坐标，还包含法向量或半径等空间信息[1-3]。但通过激光扫描等方法获得的原始数据，即点云数据，只含有三维坐标的空间信息，点云模型的离散点的法向量和半径等属性是预先计算出来的，这需要很多时间，特别就大规模的点云模型而言；而且对于曲率变化大或支离破碎的模型，计算的离散点的法向量极有可能不一致，即造成光照计算的错误（不一致）。本文提出基于最近离散点的光线跟踪算法，直接对原始的点云模型进行光线跟踪，主要贡献有以下3项：

1）对原始的点云模型进行光线跟踪，不需计算离散点的法向量和半径等信息，因此，减少了内存开销。对于无法加载的大规模的点云模型（含法向量）或网格模型到内存进行绘制的情况，本文算法在内存的容量限制下仅加载上述模型的坐标信息，并在较少的时间内，完成光线跟踪，同时保证光线与离散点的局部表面交点的法向量的一致性（即使模型的曲率变化大或者是支离破碎的模型），从而产生光照一致的高质量的图像。

2）通过改变光线跟踪的参数（最近离散点的数目），即可达到渐进地多分辨率显示原始的点云模型的目的。对于噪声多的原始的点云模型，设置较大的最近离散点的数目，以有效地减少其绘制的噪声；对于噪声少的原始的点云模型，设置较小的最近离散点的数目，以更多地显示其局部几何特征。

3）通过平衡二叉树在设定范围内搜索离光线迭代点最近的N个离散点，并用栅格的加速结构避免不必要的迭代搜索计算，提高了光线跟踪的时间效率。

1 以前的工作

目前，许多学者提出有效的方法来计算光线与点云表面的交点[4-8]，我们列出一些主要的点云模型的光线跟踪的方法如下：

Schaufler和Jenson[4]将光线想象成具有一定半径的的圆柱，通过计算圆柱前面的一些点的位置和法向量的平均值得到交点，此方法需要半径更大的圆柱来避免空洞。这将需要更多的交点计算时间，并且降低了绘制质量。

Adamson和Alexa[5]提出基于光线上的迭代点到多项式拟合的逼近表面投影的高度差的求交算法。这个方法能获得非常高的绘制质量，但它的计算成本很高。

Wand和Strasser[6]将光线考虑成各向异性的圆锥，通过光线的圆锥体与点云的多分辨率层次中预滤波的采样点相交来计算交点，算法提供了没有走样的图像，但计算时间很长。

Wald和Seidel[7]提出基于点云的隐式表面的光线跟踪的框架。他们使用在光线迭代点周围的Splats（具有圆心、半径和法向量属性的圆平面）的圆心和法向量的平均来定义局部平面逼近函数，计算光线上等间隔的点的函数值。通过在不同符号的函数值的两个迭代点插值计算得到交点。

Linsen等人[8]在Splat（定义同上）产生时，计算Splat的法向场。当光线与表面的求交时，通过Splat的法向场插值得到交点的法向量。此方法能得到光滑的显示效果。

以上点云模型的光线跟踪算法都增加了某些点元的属性，如法向量、半径、包围球内点云的拟合表面的多项式系数、点云的层次信息和Splat的法向场等，这将需要更多的内存空间和预处理时间。本文直接对原始的点云模型进行光线跟踪，因此，减少了内存开销，并且计算时间较少。

Hart[9]提出光线迭代点到隐式表面的距离作为高度差和步长的基于球体范围的光线跟踪算法。Adamson[5]等提出基于点云模型的多项式逼近表面的高度差的求交算法。本文方法也提出高度差和步长的概念，与之不同的是，当光线迭代点在离它实际最近的N′个离散点的包围球内时，本文定义迭代点到这些离散点的局部平面的垂直距离为高度差，并取其一半作为步长，而且具体迭代求交的过程和局部平面的计算也不同。

2 基于最近离散点的光线跟踪

2.1 基于最近离散点的光线跟踪算法的框架

本文首先给出基于最近离散点的光线跟踪算法的基本思想如下：

1）计算原始的点云模型的平衡二叉树的存储结构和栅格的空间信息。

2）光线迭代点逐步向点云模型的局部表面逼近，并使光线直接穿过没有离散点的空栅格。

3）用平衡二叉树在设定范围内搜索离光线迭代点最近的N个离散点，并计算实际离迭代点最近的N′个离散点的局部平面。若光线与局部平面满足相交条件，得到交点；否则，计算下一个迭代点。

2.2 点云模型的局部平面的定义

当光线上的迭代点Ai逼近点云局部表面时，以Ai为圆心、R′为半径的包围球包含N′个离散点，即点云模型中离Ai最近的N′个离散点。计算N′个离散点的包围球的球心为离散点k的坐标；并计算o到N′个离散点中最远点的距离作为包围球的半径r，如图1所示。

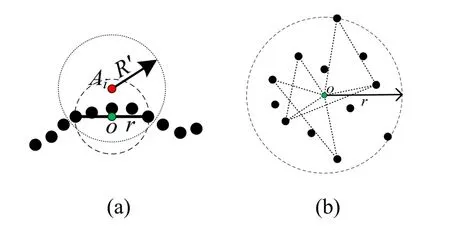
图1 离迭代点Ai最近的N′个离散点的局部表面(a)和对应的局部平面(b)

设离迭代点Ai最近的N′(N′≥3)个离散点对应的局部平面过包围球的球心o，其法向量为n。⊿oPiPj是以球心o和N′个离散点中的两个点Pi和Pj为顶点的三角形，其中j= (i+1) modN′，即⊿oPiPj的顶点Pi和Pj的顺序是按N′个离散点在最大堆（搜索最近离散点时用的堆结构）的结点顺序。

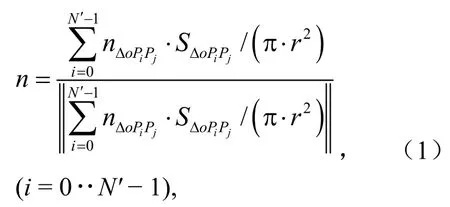
其中，SΔoPiPj和nΔoPiPj分别为⊿oPiPj的面积和法向量。令noAi为o到迭代点Ai的法向量，即，使nΔoPijP的方向与noiA一致，即：

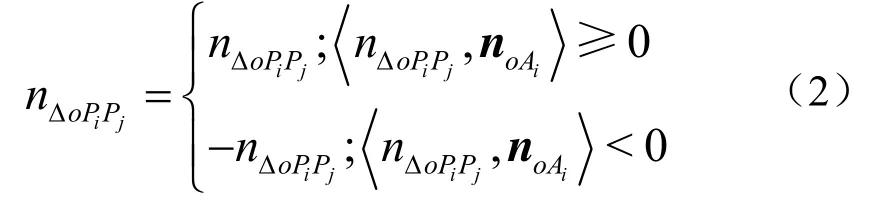
＜,＞为向量内积运算，以下均同。SΔoPiPj由海伦公式求得，nΔoPiPj由⊿oPiPj两条边的单位向量的叉积求得的向量经单位化得到。迭代点Ai沿光线方向逐步向点云模型的局部表面逼近（详见下节），确保Ai总是在点云表面的一侧，即法向量noAi的方向相对于点云表面是一致性的。SΔoPiPj越大，则nΔoPiPj对局部平面的法向量n的计算贡献越大，因此，取SΔoPiPj为nΔoPiPj的权值。通过式（1）和式（2），计算的局部平面的法向量n相对于点云表面是一致性的，并且是连续的，从而保证了高质量的绘制效果。

2.3 基于最近离散点的光线跟踪算法

本文采用平衡二叉树搜索最近的N个离散点（光子映射中多用平衡二叉树搜索空间中某点的最近若干光子[10]）。平衡二叉树中的每个结点对应点云模型的一个离散点，按结点的垂直于某坐标轴的分裂面的值（即离散点的对应坐标的值），相应空间的离散点被分成左、右两个子树，即左子树中离散点的对应坐标的值小于该分裂面的值，而右子树中离散点则相反。这样从根结点开始，搜索离迭代点Ai最近的N个离散点时，相对于分裂面，在每个结点可以排除一半不必要的搜索的点。因此，平衡二叉树的搜索效率很高，同时，初始的搜索半径R越小，则搜索效率越高[10]。

搜索算法使用最大堆存放离迭代点Ai实际最近的N′个离散点。最大堆采用平衡二叉树的结构，其中每个结点的关键值（Ai与相应离散点的距离）比左、右两子结点大。搜索算法如下：

//d初始为最大搜索半径R，堆的结点个数为N；

// 调用LocatePoints(1)，即从根结点开始搜索离迭// 代点Ai最近的N个离散点；

// 返回离迭代点Ai实际最近的N′个离散点在堆中。

LocatePoints(p)

{

if (2p+1 ＜ 点云的离散点的总数目)

{

令δ为迭代点Ai到结点(离散点)p的分裂面的距离;

if (δ＜ 0) {

LocatePoints(2p); // 迭代点Ai在左子树,

// 先遍历左子树;

if (δ2＜d2) // 检查右子树;

LocatePoints(2p+ 1); }

else {

LocatePoints(2p+ 1); // 迭代点Ai在右子树,

// 先遍历右子树;

if (δ2＜d2) // 检查左子树;

LocatePoints(2p); }

}

δ2为迭代点Ai到结点(离散点)p的平方距离;

if (δ2＜d2) {将结点(离散点)p插入最大堆中;d2= 迭代点Ai到最大堆根结点的平方距离;}

}

对点云模型的包围盒进行栅格化，每个栅格对应一个布尔变量，即当栅格中有离散点时设为真，否则设为假。这样可以减少算法在点云空间的迭代搜索的计算量，因为光线上的迭代点Ai直接跳过空栅格（没有离散点的栅格），不用在空的栅格中搜索最近的离散点，故能提高效率。

图2 光线上的迭代点Ai逐步逼近点云局部表面(a)，Ai不在(b)和在(c)最近N′个离散点的包围球内的情况

当光线上的迭代点Ai在某一非空栅格（有离散点的栅格）中，对于点云模型的所有离散点，通过平衡二叉树中在最大半径R范围内搜索离Ai最近的N个离散点，得到实际最近的N′个离散点。若N′为零，以最大搜索半径R为步长沿光线方向前进，直至逼近点云局部表面，如图2(a)所示。当N′大于零时，即光线上的迭代点Ai接近点云局部表面，分为两种情况。

第1种情况，如图2(b)所示，迭代点Ai不在N′个离散点的包围球（球心半径r为o到N′个离散点中最远点的距离，Pk为离散点k的坐标）内，即光线不与此包围球相交。因此，光线不与包围球内的点云局部表面相交，计算下一个迭代点Ai+1。

第2种情况，如图2(c)所示，迭代点Ai在N′个离散点的包围球内，即光线与此包围球相交，判断是否满足光线与点云局部表面相交的条件。若满足相交的条件，得到相应的交点；否则，计算下一个迭代点Ai+1。

光线与点云局部平面相交的情况如图3所示，设光线与过球心o、法向量为n（n的计算见上节）的局部平面相交于B。若Ai与B的距离和半径r的比值小于阈值α时，或Ai到局部平面的垂直距离与r的比值小于阈值β时，则光线与点云局部表面相交，即相交的判断条件为：

图3 光线与点云局部平面（过点o、法向量为n）相交于B点，h为Ai到局部平面的垂直高度

若光线与原始的点云模型相交，布尔变量intersect被设置为TRUE；否则，它被设置为FALSE。具体求交算法如下：

输入：原始的点云模型、平衡二叉树、栅格、最大的搜索半径R、最近的离散点个数N、阈值α和β

输出：布尔变量intersect，交点的坐标和法向量

步骤1计算光线与点云包围盒的交点，若有交点，即光线迭代点A0，转到步骤2；否则，返回intersect= FALSE。

步骤2计算光线迭代点Ai所在的栅格，若栅格在点云包围盒外，返回intersect= FALSE；否则，判断当前栅格是否有离散点，若无，计算光线与邻近栅格的交点作为下一个迭代点Ai+1，转到步骤2，若有，转到步骤3。

步骤3对于点云模型的所有离散点，利用平衡二叉树在最大搜索半径R的范围内搜索离迭代点Ai最近的N个离散点，得到实际的N′个最近的离散点（见上面的LocatePoints(p)算法）。

步骤4若N′= 0，则Ai以步长R沿光线方向计算下一个迭代点Ai+1，转到步骤2；否则，转到步骤5。

步骤5若N′＜ 3，则计算Ai到N′个离散点中最近点的距离，取其一半作为步长，沿光线方向计算下一个迭代点Ai+1，转到步骤2；否则，转到步骤6。

步骤6若迭代点Ai不在N′个离散点的包围球内，则计算Ai到其中最近点的距离，取其一半作为步长，沿光线方向计算下一个迭代点Ai+1，转到步骤2，如图2(b)所示；否则，转到步骤7，如图2(c)所示。

步骤7由式（1）和式（2）计算过包围球圆心的局部平面的法向量n，并计算光线与局部平面的交点B（见图3）。若满足条件式（3），则得到相应的交点即为B，其法向量即为n，返回intersect= TRUE；否则，以迭代点Ai到局部平面的垂直距离h的一半作为步长，沿光线方向计算下一个迭代点Ai+1，转到步骤2。

上述算法通过改变光线跟踪的参数（最近离散点的数目），即可渐进地多分辨率显示原始的点云模型。对于噪声多的原始的点模型，设置较大的最近离散点的数目，以有效地减少其绘制的噪声；对于噪声少的原始的点模型，设置较小的最近离散点的数目，以更多地显示其局部几何特征。

3 实验设计和结果

本文所有实验都在单个的Intel (R) 2.66GHz CPU平台上执行的。所有的点云模型都是从www.dirdim.com网站下载的免费的点云数据文件，即只包含三维坐标信息。点云模型的离散点的数目如表1所示。

表1 4个点云模型的离散点的数目

实验的设置参数：栅格数目NGd、离散点的最大搜索半径R、最近的离散点个数N、光线迭代点与局部平面的光线交点的距离和包围球半径比值的阈值α、迭代点到局部平面的垂直距离与包围球半径比值的阈值β（详见2.3节）。设L为点云模型的包围盒的X、Y和Z轴长度和。

实验的结果数据：实际最近离散点的平均非零个数N′、平衡二叉树的建立时间TSetTree、栅格的建立时间TSetGd、点云模型的光线跟踪时间TRay、计算时间的总和TTotal(即TTotal=TSetTree+TSetGd+TRay)。

本文对点云模型Demo Head和Facility Scanning的实验参数N分别设置不同的值，得到相应的实验结果。所有点云模型的实验参数的设置如表2所示，其光线跟踪实验的结果统计如表3所示。

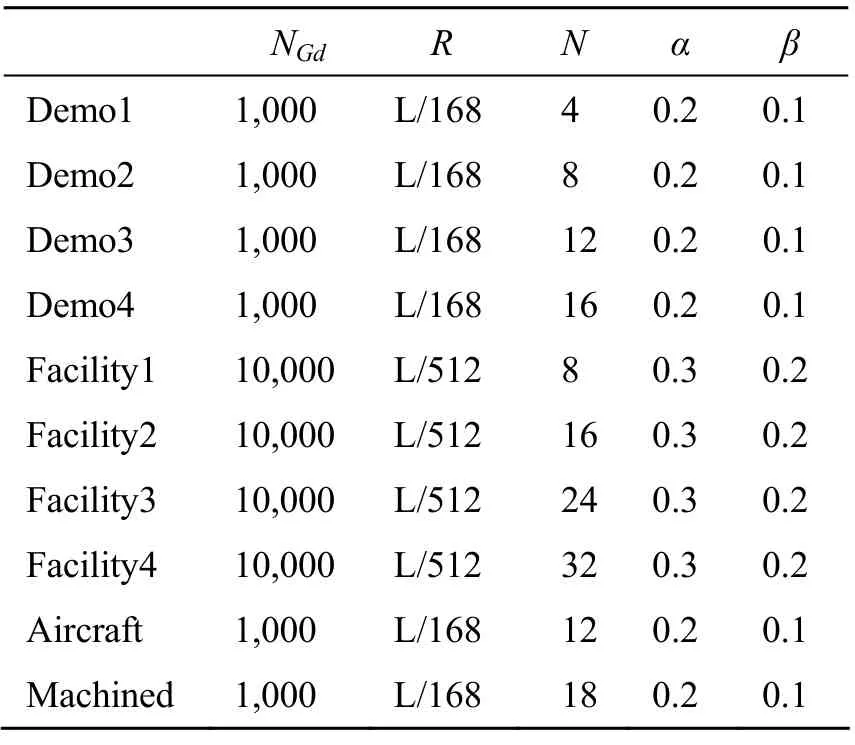
表2 点云模型的光线跟踪实验的设置参数

在图4-6中，原始的点云模型的光线跟踪生成图像的分辨率都为400×500像素。通过设置迭代点的最近离散点的不同的个数N，即当N逐渐变大（即4、8、12、16），点云模型Demo Head的绘制效果变得更光滑，同时，点云表面的一些细节部分变得模糊，相应的光线跟踪时间也增多（见表3）。如图5所示，当N逐渐变大（即8、16、24、32），点云模型Facility Scanning的绘制的噪声逐渐减少。由图4和图5可见，对于噪声少的模型（如Demo Head），可以设置较小的最近离散点个数，以更多地保留其局部几何特征；对于噪声多的模型（如 Facility Scanning），设置较大的最近离散点个数，以有效地减少其噪声。

图4 原始的点云模型的光线跟踪的绘制效果（400×500像素）

图6 原始的点云模型的光线跟踪的绘制效果（400×500像素）

表3 点云模型的光线跟踪实验的结果统计（时间单位：毫秒）

光线迭代点的实际最近离散点的个数N′略小于设置的值N，这是由于迭代点逐渐逼近点云表面并且最大搜索半径R的范围的限制（详见2.3节）。点云模型Facility Scanning的离散点的数目远大于其它的点云模型，因此，相应的计算时间也更多（见表3）。由图4-6可见，对于原始的点云模型，在较少的时间内（见表3），本文的算法能产生高质量的绘制效果。

4 结 论

本文提出了基于最近离散点的光线跟踪算法，即在较少的时间内，直接对仅包含三维坐标的点云模型进行光线跟踪，不需计算离散点的法向量和半径等信息。算法保证了光线与局部平面的交点的法向量计算的一致性，从而产生十分满意的绘制效果。

本文算法通过改变光线跟踪的参数（最近离散点的数目），即可达到渐进地多分辨率显示原始的点云模型的目的。对于噪声多的原始的点模型，设置较大的最近离散点的数目，以有效地减少其绘制的噪声；对于噪声少的原始的点模型，设置较小的最近离散点的数目，以更多地显示其局部几何特征。

今后，计划将本文的算法扩展到GPU上，达到实时交互的目的。

[1]Levoy M, Whitted T. The use of points as display primitives [J]. Technical Report 85-022, Computer Science Department, University of North Carolina at Chapel Hill, 1985.

[2]Kobbelt L, Botsch M. A survey of point-based techniques in computer graphics [J]. Computers &Graphics, 2004, 28(6): 801-814.

[3]Sainz M, Pajarola R. Point-based rendering techniques [J].Computers & Graphics, 2004, 28: 869-879.

[4]Schaufler G, Jensen H W. Ray tracing point sampled geometry [C]//Proceedings of the 11th Eurographics Workshop on Rendering, 2000: 319-328.

[5]Adamson A, Alexa M. Ray tracing point set surfaces [C]//Proceedings of the Shape Modeling International,2003: 272-279.

[6]Wand M, Strasser W. Multi-resolution point-sample raytracing [C]//Graphics Interface, 2003: 139-148.

[7]Wald I, Seidel H P. Interactive ray tracing of point-based models [C]//Eurographics Symposium on Point-Based Graphics, 2005: 1-8.

[8]Linsen L, M¨uller K, Rosenthal P. Splat-based ray tracing of point clouds [J]. Journal of WSCG, 2007,15(2): 51-58.

[9]Hart J C. Sphere tracing: a geometric method for the antialiased ray tracing of implicit surfaces [J]. The Visual Computer, 1996, 12(9): 527-545.

[10]Jensen H W. Realistic image synthesis using photon mapping [M]. A.K.Peters; 2001.