非磁性界面光波磁场量的菲涅耳公式*
谭长明,范希智,成云舟,易迎彦,陈清明,祝霁洺
(1.鞍山师范学院 商学院,辽宁 鞍山 114005;2.武汉理工大学 物理系,湖北 武汉 430070)
引 言
光波是电磁波,是高频振荡的电场矢量E和磁场矢量H在空间的传播。在传播过程中遇到界面时,光波要发生变化,产生分光,即一般会出现反射光和折射光。反射光波和折射光波的传播方向与原光波的传播方向之间的变化遵从反射、折射定律。而反射光波和折射光波的电场与原光波的电场在量值上的变化关系则由菲涅耳公式来表达[1-11]。由维纳驻波等很多实验证明了光与非磁性物质相互作用时,起很明显作用的是电场E,磁场H的作用则很微弱,理论上也说明了这一点,因而人们主要关注光波中电场E的变化,往往不考虑磁场H的变化。但无论如何,当光传播遇到界面时,反射光波和折射光波的磁场H是一定发生了变化的,所以只关注光波中电场E的变化是不全面的。关于电场E的菲涅耳公式并未完全反映光波在界面上的变化情况,因此必须考察磁场H的变化,针对其变化规律,本文进行了较为详细的讨论,得出对应于光波磁场量的菲涅耳公式,以全面反映光波在界面的变化规律。
1 光波磁场量的菲涅耳公式
为简单起见,只讨论平面光波(以下简称光波)遇到两种各向同性透明的非磁性均匀媒质的界面时磁场H的变化规律。因为光波中磁场H和电场E是同时存在的,因而讨论磁场的变化需借助电场量的变化。电场E和磁场H都是矢量,对于每个矢量,都可将其分解为一对正交的场矢量分量,其中一个分量的振动方向垂直于入射面,称为‘s’分量;另一个分量的振动方向在或者说平行于入射面,称为‘p’分量,首先研究入射波仅含‘s’分量和仅含‘p’分量这两种特殊情况。当两种分量同时存在时,则只要分别先计算由单个分量成分的折射、反射场量,然后根据矢量叠加原理进行矢量相加即可得到相应的结果。在讨论的时候不妨规定:电场和磁场的s分量垂直于纸面,向外为正,向内为负;而规定电场和磁场的p分量按其在界面上的投影方向,向右为正,向左为负。
1.1 磁场p分量的反射系数和透射系数
当入射光波只有s电场分量时,反射波和折射波也只有s电场分量,不妨假设其方向均为正,如图1所示。根据E、H、k(k为波矢,其方向代表光波传播的方向)符合右手定则的要求来确定三个波的磁场方向,此时只存在入射、反射和折射光波磁场H的p分量:Hip、Hrp和Htp。根据E、H在界面上的切向分量连续的边界条件:n×(E2-E1)=0,n×(H2-H1)=0(其中E1、E2和H1、H2分别为媒质1和媒质2中的光波电场和光波磁场)可以得到标量形式:
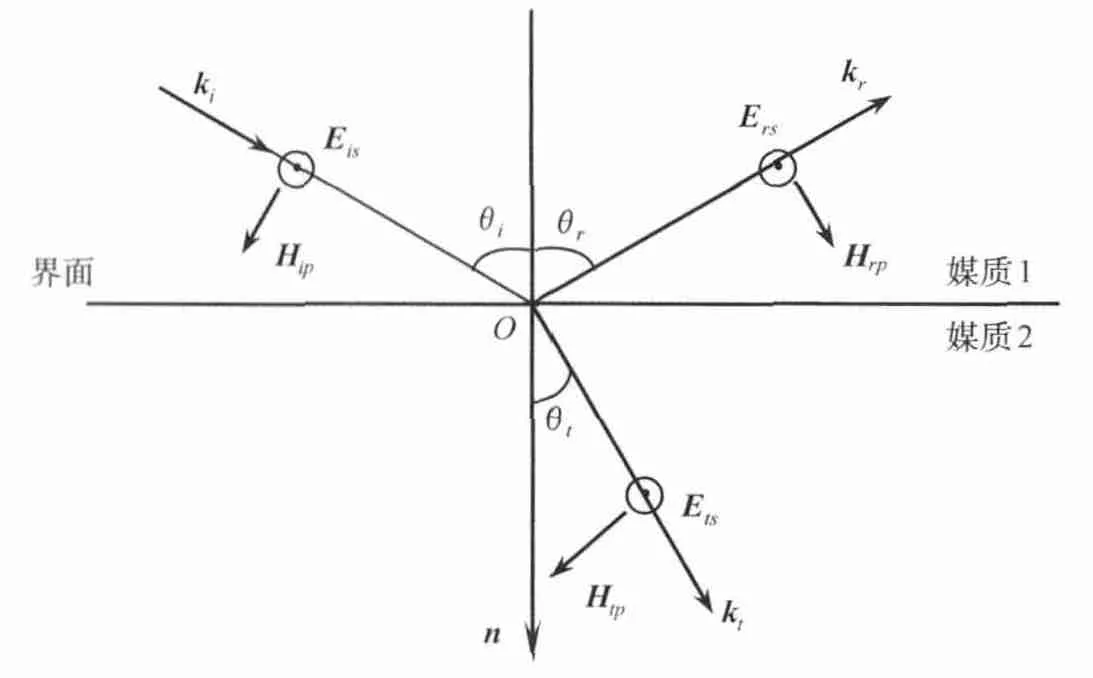
图1 入射光波只有s电场分量时的正向规定Fig.1 The positive direction supposition when the incident light has only s electrical field component
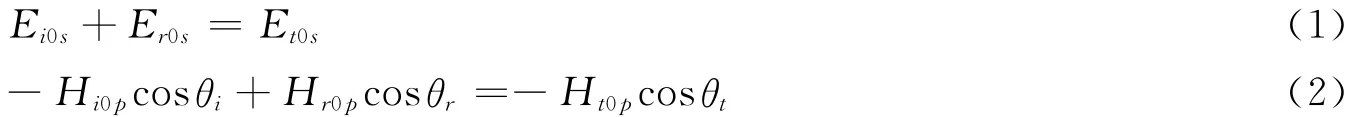
其中θi、θr和θt分别为入射角、反射角和折射角。在非磁性各向同性介质中,E、H之间的量值的关系为:

其中n为所在媒质的折射率,μ0为真空中的导磁率,c为真空中的光速。再考虑到E、H的正交关系,式(1)可以变成含有H的另外一个形式:

联合式(2)和式(4),利用反射定律θr=θi,可以得到H的p分量的反射系数rHp和透射系数tHp:
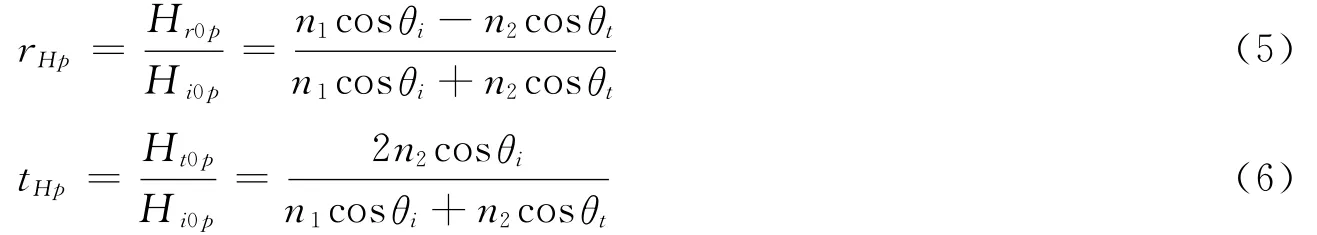
1.2 磁场s分量的反射系数和透射系数
同样,当入射光波只有p电场分量时,反射波和折射波也只有p电场分量。不妨假设E的p分量对于界面的切向分量一致向右,则入射、反射和折射光波的E的p分量取向如图2所示,根据E、H、k组成右手坐标系的原则,此时只存在入射、反射和折射光波磁场H的s分量:His、Hrs和Hts,图2中也标示了它们的方向。利用E、H的边界条件,得:
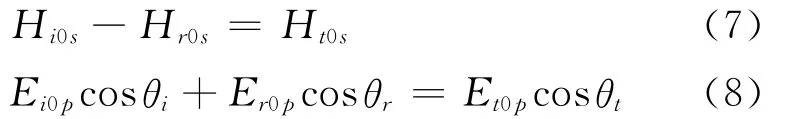
再利用式(3)以及E、H 之间的正交性,式(8)可变成含有H的另外一个形式:
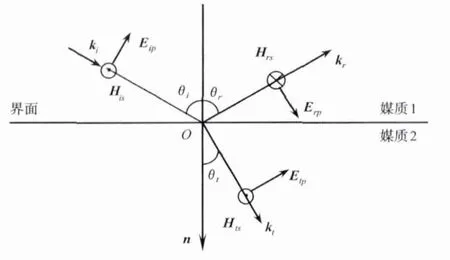
图2 入射光波只有p电场分量时的正向规定Fig.2 The positive direction supposition when the incident light has only pelectrical field component
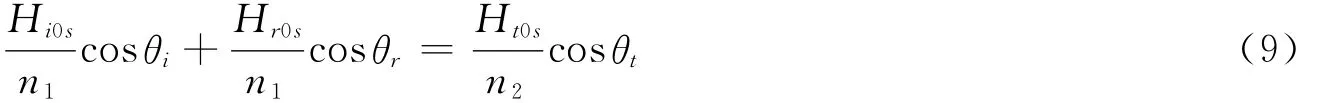
联合式(7)和式(9),利用反射定律θr=θi,可得H的s分量的反射系数rHs和透射系数tHs:
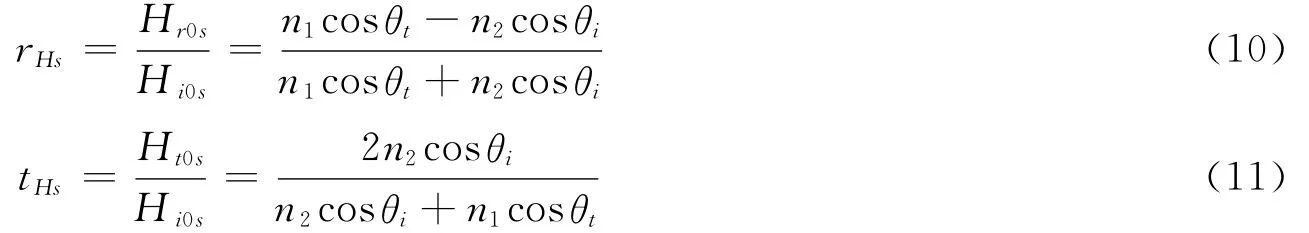
类似于光波电场的菲涅耳公式,不妨称式(5)、式(6)、式(10)、式(11)为非磁性界面光波磁场量的菲涅耳公式。
2 讨 论
本节首先讨论磁场量的菲涅耳公式与光波电场量的菲涅耳公式的关系。光在界面上反射和折射时,有两个重要的现象出现,其一就是π位相跃变的产生,其二则是布儒斯特现象的发生,本节接下来利用光波磁场量的菲涅耳公式对这两个现象进行解释,之后从光波磁场量的角度讨论一下光波正入射的情况。
2.1 两组公式的关系
将光波磁场量的菲涅耳公式式(5)、式(6)、式(10)、式(11)与光波电场量的菲涅耳公式[2]相比较,不难发现,磁场量s分量的反射系数rHs和电场量p分量的反射系数rEp相同;而磁场量p分量的反射系数rHp和电场量s分量的反射系数rEs相同。
作为举例,图3(a)绘出了光从空气(n1=1)中射入玻璃(n2=1.5)时rHs、rHp、tHs和tHp随入射角θi的变化曲线,即按磁场量菲涅耳公式绘制的曲线;图3(b)绘出了光从空气(n1=1)中射入玻璃(n2=1.5)时rEs、rEp、tEs和tEp随入射角θi的变化曲线,即按电场量菲涅耳公式绘制的曲线。表1则列出了一些具体入射角下各个系数按相应公式计算的具体数值。由图3和表1可以看到:rHs=rEp;rHp=rEs。
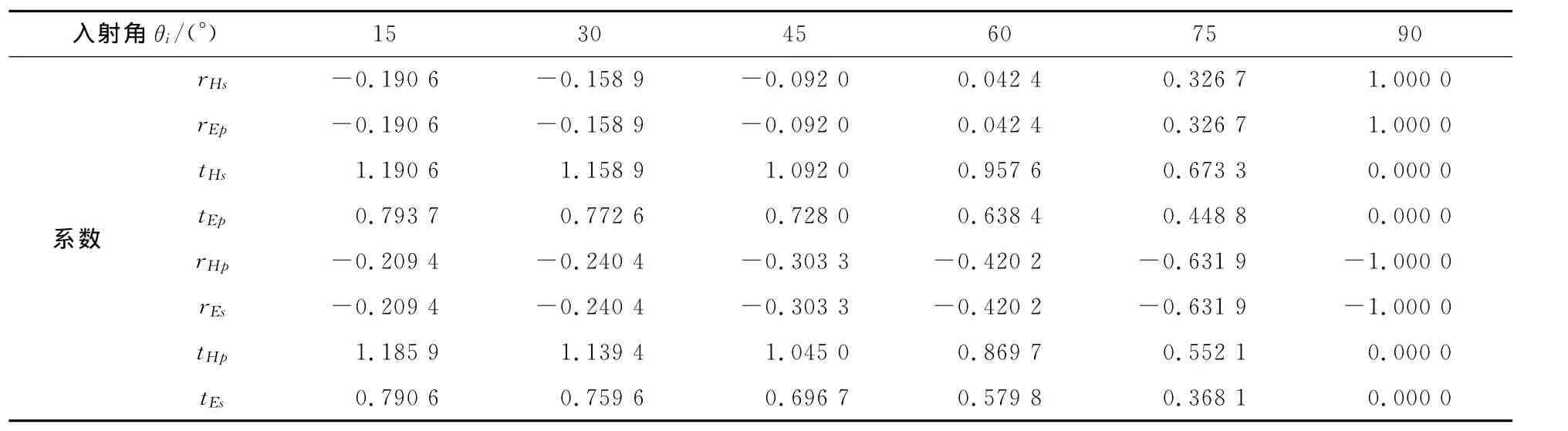
表1 一些具体入射角下各个系数的具体数值Tab.1 Coefficient values at some incident angles
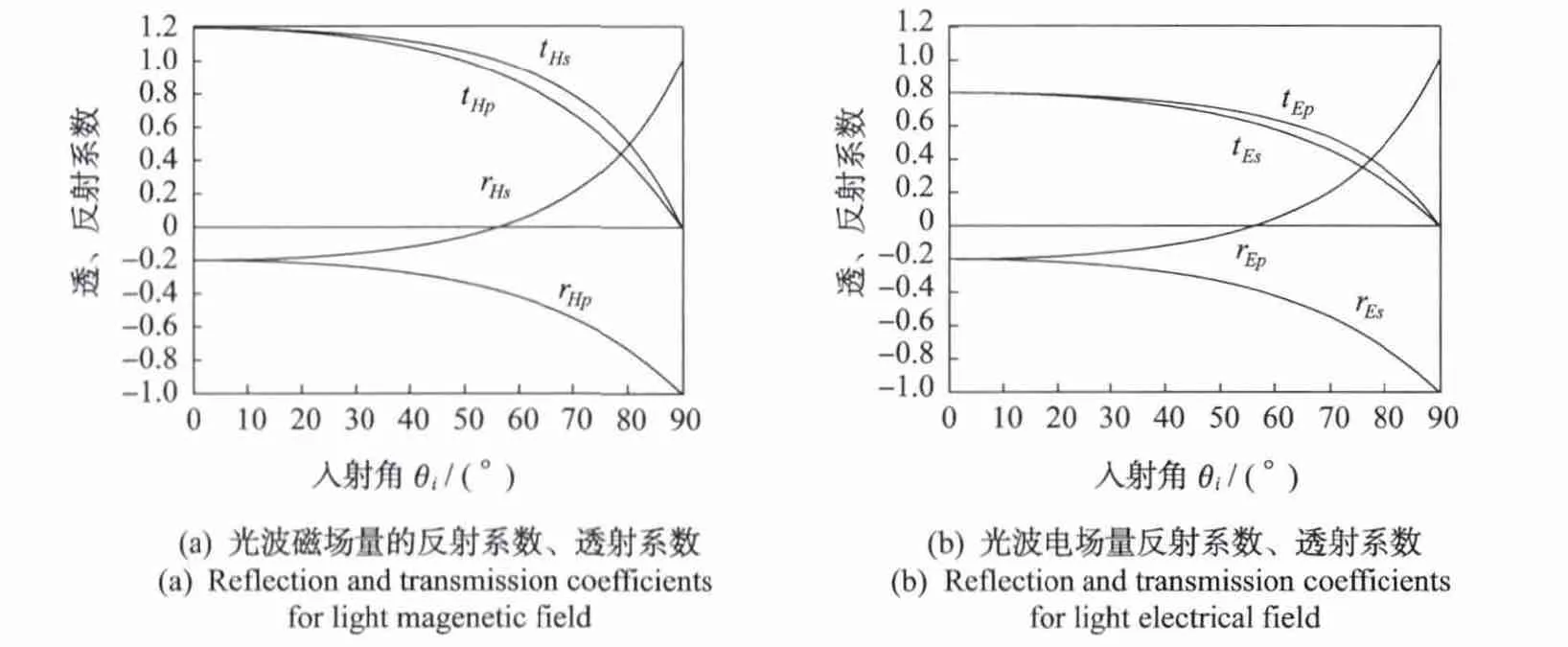
图3 反射系数、透射系数随入射角θi变化的曲线Fig.3 Curve of reflection and transmission coefficients with angleθiof incidence
由表1和图3可以看到,磁场量s分量的透射系数tHs不同于电场量p分量的透射系数tEp,前者为后者的1.5倍;磁场量p分量的透射系数tHp也同于电场量s分量的反射系数tEs,前者为后者的1.5倍。再系统比较两组菲涅耳公式,发现透射系数的比值是固定的,即

对于光从空气(n1=1)中射入玻璃(n2=1.5)的具体情况,即为表1和图3显示的结果。不难理解透射系数之间存在的式(12)所示的关系。根据E、H、k符合右手定则的要求,结合式(3)及透射系数的原始定义式(6)和式(11)的左半部等式,容易得到:

将上两式合并即为式(12),由此即得两组透射系数的关系,并得以解释。
因为光波是矢量电磁波,既可用电场E的变化来标征,也可用磁场H的变化来标征。当用电场E来标征时,光通过界面时出现的反射光、折射光在量值上变化就要用电场值的变化来表示,即由电场量的菲涅耳公式来表示。若光波用磁场H来标征,则反射光、折射光在量值上变化就要用磁场量的菲涅耳公式来表示。所以,光波磁场量的菲涅耳公式与光波电场量的菲涅耳公式等价。但是,无论电场E还是磁场H,都是表征光波的一个方面,从这个角度来看,这两组公式又是相互补充的。
2.2 π位相跃变的解释
当光波从光疏媒质通过界面射入光密媒质时,反射光波的电场s分量与原入射光波的电场s分量Eis反向,即rEs<0,称这种现象为π位相跃变[1-9,12]。这个效应也可从磁场H 角度来解释,根据式(5),在光波从光疏媒质通过界面射入光密媒质的情况下,n1<n2,90°≥θi>θt≥0°,则cosθi<cosθt,所以n1cosθi<n2cosθt,所以rHp<0,说明反射光磁场的p分量与与原入射光波的磁场p分量Hip反向,反射光的传播方向即kr的方向是由反射定律确定的,而Er、Hr与kr之间的方向关系由右手定则确定的,光波磁场的只有p分量时,电场只有s分量,即Ers、Hrp与kr符合右手定则,可见Hrp与Hip反向,Ers肯定与Eis反向,即有π位相跃变。
2.3 布儒斯特现象的解释
当光波以某一角度θB入射时,反射光电场量的p分量为零,只存在电场量的s分量,这种现象称为布儒斯特现象,相应的入射角θB称为布儒斯特角,θB与界面两侧媒质的折射率n1、n2的关系为:

布儒斯特现象也可从磁场H角度来解释。根据式(10),当光波从光疏媒质通过界面射入光密媒质时,n1<n2,90°≥θi>θt≥0°;当光波从光密媒质通过界面射入光疏媒质时,n1>n2,90°≥θt>θi≥0°,如论如何,总有一个入射角出现,使得式(10)的分子为零,即使n1cosθt=n2cosθi。此时rHs=0,结合折射定律(n2sinθt=n1sinθi)即可求得这个特殊的入射角即为布儒斯特角θB。
在以θB入射时,rHs=0,说明反射光波磁场量的s分量为零,只存在磁场量的p分量。而光波磁场量H与电场量E是相互垂直的,即Er、Hr与kr之间的方向符合右手定则,根据这个要求可知,反射光波的电场量的p分量为零,只存在电场量的s分量,即发生了布儒斯特现象。
2.4 正入射的情况
当光波正入射界面时,磁场量的菲涅耳公式式(5)、式(6)、式(10)、式(11)将简并,变为:

可见,在正入射时,光波磁场量的两个反射系数、两个透射系数相等。特别是,当光波从光疏媒质通过界面正入射光密媒质时,n1<n2,rHs、rHp<0,可见,反射光磁场矢量的s分量与入射光磁场的s分量反向,反射光磁场矢量的p分量与入射光磁场的p分量反向,因而反射光磁场矢量与入射光的磁场矢量反向由于光波磁场矢量垂直于电场矢量。反射光电场矢量与入射光的电场矢量也反向,即产生π位相跃变。
总之,通过前面的讨论可知,光波磁场量的菲涅耳公式具有实用性,可以用来解释光波通过界面时出现的π位相跃变效应和布儒斯特现象等重要的特征。这组公式等价于电场量的菲涅耳公式,有助于人们全面理解光通过非磁性光学界面时的规律,因而具有一定的重要性,只是由于光与非磁性物质相互作用时,起很明显作用的是电场E,磁场H的作用则很微弱,因而光波磁场量的菲涅耳公式往往一些教科书中被忽略不讲[1-9]。
3 结 论
根据E、H、k符合右手定则尤其E垂直于H的实际,利用非磁性各向同性介质中E与H之间的数值的关系,结合E、H在界面上的切向分量连续的边界条件,本文推导了光波在非磁性光学界面上磁场量H的s分量的反射系数rHs、透射系数tHs和p分量的反射系数rHp和透射系数tHp的表达式,即得出非磁性光学界面上磁场量H的菲涅耳公式,该组公式与非磁性光学界面上电场量E的菲涅耳公式是等价的;其中rHs等于电场量E的p分量的反射系数rEp;而rHp等于电场量E的s分量的反射系数rEs。利用rHs和rHp,也可以解释光波在非磁性光学界面上分光(即反射和折射)时出现的π位相跃变效应和布儒斯特效应等重要的现象。非磁性光学界面上磁场量H的菲涅耳公式有助于人们全面理解光通过非磁性光学界面时的分光规律,因而是重要的。
[1]梁铨廷.物理光学[M].3版.北京:电子工业出版社,2008:22-31.
[2]谢敬辉,赵达尊,阎吉祥.物理光学教程[M].北京:北京理工大学出版社,2005:32-44.
[3]范少卿,郭富昌.物理光学[M].北京:北京理工大学出版社,1990:19-30.
[4]王 楚,汤俊雄.光学[M].北京:北京大学出版社,2001:28-34.
[5]赵达尊,张怀玉.波动光学[M].北京:宇航出版社,1988:51-59.
[6]姚启钧.光学教程[M].北京:高等教育出版社,1981:34-39.
[7]潘笃武,贾玉润,陈善华.光学(上册)[M].上海:复旦大学出版社,1997:41-55.
[8]廖延彪.光学原理与应用[M].北京:电子工业出版社,2006:38-55.
[9]钟锡华.现代光学基础[M].北京:北京大学出版社,2003:118-121.
[10]郭 军.菲涅耳公式的验证性实验[J].物理实验,2009,30(2):40-43.
[11]文盛乐,易慧先.介质表面运动时的菲涅耳公式[J].大学物理,2001,20(11):5-8.
[12]范希智,祝霁洺.分振幅双光束等倾干涉中半波损失的讨论[J].光学仪器,2012,34(5):54-60.

