三相瞬时功率理论在有源电力滤波器仿真中的研究＊

韩 建，邢志方，何学兰，魏运锋

（1.东北石油大学 电子科学学院，黑龙江 大庆 163318；2.东北石油大学 黑龙江省高校校企共建测试计量技术及仪器仪表工程研发中心，黑龙江 大庆 163318）

引 言

随着电网中非线性负载的大量使用，其产生的谐波对电网中其他用电设备的影响日趋严重，尤其是一些对电源噪声非常敏感的光源类设备，如半导体激光器、低压汞灯等［1］。为了治理电网谐波，电力滤波器在电力行业得到了广泛的应用，电力滤波器分无源和有源两种，有源电力滤波器（active power filter，APF）突出的优点是能跟踪变化的谐波，实现快速、准确的谐波补偿。有源电力滤波器需要对电网谐波进行实时跟踪检测，谐波检测一般通过将采样的电压、电流进行特定算法计算得到，因此算法好坏将直接影响到有源电力滤波器的谐波补偿效果［2］，本文对基于MATLAB／Simulink平台上仿真的模型，通过仿真对该算法进行验证，为深入研究瞬时功率理论在有源电力滤波器中的应用提供了有益的参考。

1 基于三相瞬时功率理论的ip－iq谐波检测算法

三相瞬时功率理论认为：任意时刻三相电路的总瞬时有功功率等于各相的瞬时有功功率相加，它代表三相电力线消耗在负载上做功的功率，瞬时无功功率仅在三相电路之间来回传递，在负载上不做功，各相瞬时无功功率之和恒等于零［3］。该理论是基于α－β两相正交坐标系的，因此需要将三相电路电压瞬时值Ua（t）、Ub（t）、Uc（t）与电流瞬时值ia（t）、ib（t）、ic（t）变换到对应两相正交坐标系的电压电流值。设三相坐标系中的各相电压瞬时值分别为ea、eb、ec，电流瞬时值分别为ia、ib、ic，两相正交坐标系下的瞬时电压分量为eα、eβ，瞬时电流分量为ia、iβ，通过下面式子进行变换：

变换后的两相值还可以通过反变换还原成三相值：

变换后的两轴瞬时电压分量为eα、eβ合成大小为辐角为φe的电压矢量e，两轴瞬时电流ia、iβ合成为大小为、辐角为φi的电流矢量i。为使用ip－iq检测方式，还需要进行从两相静止的α－β坐标系到两相旋转的p－q坐标系变换，将两个坐标系的原点重合，令p轴的方向和电压矢量e相同［4］，如图1所示。

电压矢量e和电流矢量i的表达式如下：

为得到ip与iq的表达式，设与电网a相电压相位与频率相同的正弦信号为sinωt，余弦信号为－cosωt［5］，则有：

再经过低通滤波之后得到ip、iq的直流分量i—p、i—q，通过2／3反变换得到电网电流ia、ib、ic的基波分量iaf、ibf、icf：

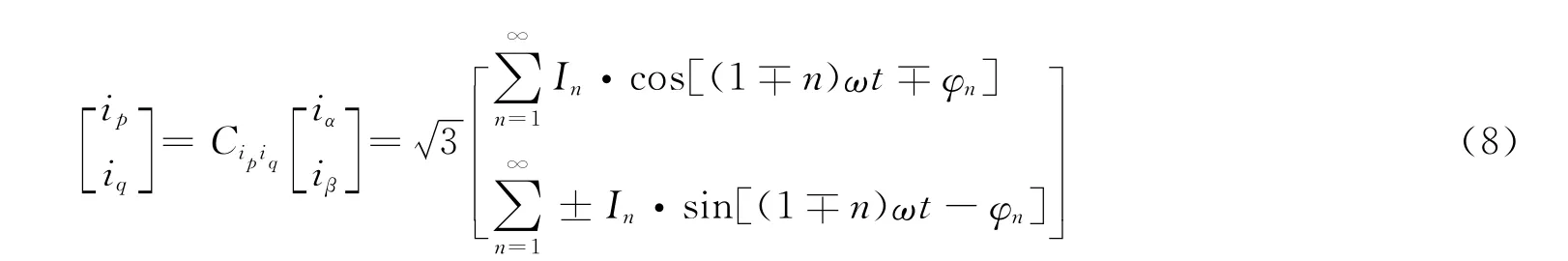
再经过两相到三相反变换得到三相基波电流：

将采样得到的原始电流信号与检测到的基波电流信号相减即得到谐波电流信号［6］。ip－iq检测方式的原理图如图2所示。

图2 ip－iq检测方式原理图Fig.2 Detection diagram of ip－iq

由于使用与电网电压相同频率与相位的正余弦电压信号sinωt和－cosωt参与谐波电流计算，避免了p－q检测方式中电网电压直接参与运算，在电网电压发生畸变时，只要正确锁定电网电压频率及相位，就能保证检测的准确性，使ip－iq检测方式具有更好的谐波环境适应性［7］。

2 谐波电流检测电路的MATLAB建模与仿真

根据图2的谐波检测流程在MATLAB的Simulink环境下搭建的谐波电路检测仿真模型如图3所示。

为验证谐波检测效果，需构建一个整体的有源电力滤波器仿真模型，有源电力滤波器是根据检测到的谐波来控制逆变电路对电网电流进行主动补偿，因此需要构建逆变控制电路［8］，这里选用比较成熟的滞环比较控制方式，该控制方式是将三相指令电流信号与三相补偿电流信号做减法，输出给六个滞回比较器以产生PWM逆变控制信号［9］。在逆变电路中，直流侧电容为谐波补偿储能电容，电容与交流侧电源电压的差值作用于电感产生补偿电流ic，开关器件采用Simulink工具箱中的IGBT模型，IGBT在滞环控制电路输出的PWM信号控制下向电网输出补偿电流。搭建好的整体模型如图4所示。

仿真电路参数为：电网电压设置为220V的三相电源；逆变器直流侧电压UDC设置为500V；导线电阻设置为1mΩ，导线电感为0.2mH。由于接入了感性负载，电网波形发生了明显的畸变，不再是正弦波，为观察与分析方便，仅取a相进行分析，畸变后的波形以及电网基波分量分别如图5（a）及图5（b）所示。

为验证谐波检测模块能否正确检测出电网基波分量，在信号i—a处接入示波器，观察到的波形如图5（b）所示。可见该算法从畸变的电网电流中有效分离出了基波分量。谐波波形实际上就是图5（a）与图5（b）波形相减的结果，下面是检测到的谐波电流与滞环比较控制方式生成的与之对应的跟踪电流波形。

图3 有源电力滤波器谐波检测仿真模型Fig.3 Harmonic detection simulation model of APF

图4 有源电力滤波器整体仿真模型Fig.4 Entire simulation model of APF

图5 畸变的电网波形及其基波分量Fig.5 Waveform of distorted grid and its fundamental wave

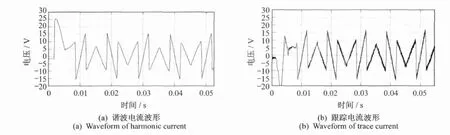
图6 谐波及跟踪电流波形Fig.6 Waveform of harmonic and trace current

图6（a）谐波电流与图6（b）跟踪电流的对比，说明滞环比较控制方式准确地对谐波电流进行了跟踪。最后，得到补偿后的三相电网电流波形如图7所示。

从图7可以看出，相对于图5（a），补偿后的波形已经非常接近正弦波了，再使用Simulink工具箱中POWERGUI的傅里叶分析工具，对补偿前后的电网电流进行频谱分析。

由补偿前后的频谱分析结果知，畸变的电网电流谐波中5次、7次、11次等谐波占主要部分，总谐波失真达到24.64%，补偿之后，这部分谐波被有效抑制，总谐波失真下降到了1.08%，补偿效果十分显著。

图7 补偿后的三相电网电流波形Fig.7 Waveform of compensated grid

图8 补偿前后电流频谱分析图对比Fig.8 Comparison of current spectrum analysis before and after compensation

3 结 论

通过基于瞬时功率理论的ip－iq谐波检测算法详细推导，可以知道该算法具有良好的谐波检测效果。使用MATLAB的Simulink工具箱建立了基于该算法的有源电力滤波器仿真模型，仿真结果表明此算法能够准确、实时地对三相电网谐波进行跟踪检测，再结合滞环比较控制方式取得了很好的谐波补偿效果，验证了前面理论工作的正确性，对有源电力滤波器的程序及电路设计有很好的参考价值。

［1］袁波江，薛大建，陆璇辉.低噪声半导体激光器驱动电源的研制［J］.光学仪器，2005，27（5）：69－71.

［2］张国荣，陈云飞.基于重复控制的三相4线制有源电力滤波器研究［J］.电气传动，2012，42（10）：35－39.

［3］AKAGI H，KANAZAWA Y，NABAE A.Generalized theory of the instantaneous reactive power and its applications［J］.Transactions of the IEE－Japan，Part B，1983，103（7）：483－49.

［4］浦志勇，黄立培，吴学智.三相PWM 整流器空间矢量控制简化算法的研究［J］.电工电能新技术，2002，21（2）：56－60.

［5］张代润，宋婷婷，陈 洲，等.有源电力滤波器的实验研究［J］.电力系统及其自动化学报，2005，17（3）：28－34.

［6］陈国柱，吕征宇，钱照明.有源电力滤波器的一般原理及应用［J］.中国电机工程学报，2000，20（9）：17－21.

［7］仲伟堂，李 标.新型控制系统的并联混合型有源电力滤波器［J］.电力电子技术，2012，46（2）：89－91.

［8］陈东华，江 晨，谢少军，等.一种适用于独立小容量交流电网的APF电流基准产生方法［J］.中国电机工程学报，2007，27（16）：92－97.

［9］杨 柳，刘会金，陈允平.三相四线制系统任意次谐波电流的检测新方法［J］.中国电机工程学报，2005，25（13）：41－44.