陷波滤光片的类褶皱设计*
高 鹏,阴晓俊,赵帅锋,吴增辉,任少鹏,费书国
(沈阳仪表科学研究院有限公司,辽宁 沈阳 110043)
引 言
陷波滤光片,也称带阻滤光片或负滤光片,其光学特性表现为:在应用波段范围内,滤光片对大部分波长的光具有良好的透射率,而对特定波长范围(阻带)内的光可进行有效截止。它能在一段光谱中去除某些特定波段,其功能恰与带通滤光片相反。在生物医疗、拉曼分析、荧光测试、激光防护等方面,陷波滤光片获得了广泛的应用。
基于褶皱(Rugate)理论可以设计出性能优越的陷波滤光片,但理论要求折射率随膜厚分布连续渐变(其折射率变化规律如图1所示),若采用传统的镀膜工艺很难实现。依据等效折射率理论,人们提出了一些近似方法。有人研究了基于三种以上材料的多膜料设计方法[1-3],可以设计一些简单的陷波滤光片,但由于可用膜料有限,此种方法受到限制;有人研究了厚度匹配层方法[3-5],但其中存在的大量超薄层给制备工艺带来了麻烦。
共镀技术(如:共蒸发技术、共溅射技术)的出现,使得人们可获得折射率介于高低折射率材料之间任一值的混合材料,这为光学薄膜膜系设计提供了新的路径。基于此技术,人们研究并提出了一些褶皱设计方法:有人研究了折射率随膜厚连续渐变的不同规律[6-11],以获得更好的陷波滤光效果,但如何精确控制折射率按预期规律连续变化仍是镀制工艺上的难题;有人研究了将折射率随膜厚渐变规律分为众多小层的方法[12-14],但对各小层中的折射率及膜厚的精准控制对镀制工艺依旧是不小的挑战。
为避免出现薄层,有人提出用规整膜系设计陷波滤光片的观点[15-16]。本文介绍折射率在本层内不变的一种类褶皱陷波滤光片设计方法,并分析各设计参数对光谱的影响。

图1 褶皱理论中折射率变化示意图Fig.1 Schematic diagram of refractive index changes in rugate theory
1 设计方法
1.1 膜系介绍
令膜系中各层的折射率按图2所示的趋势变化。

图2 陷波滤光片类皱褶设计膜系的折射率随层数的变化规律示意图Fig.2 Schematic diagram of refractive index changes with layers in quasi-rugate method of notch filter
可以看到,随着层数的增加,高低折射率之间的差值逐渐增大,当差值达到最大时堆叠s次,然后差值又逐渐减小。膜系中每一层均为均匀薄膜,且均为1个光学厚度。折射率的这种变化趋势与褶皱理论不同,却又有一定的相似性,可称为类褶皱设计方法。由于不需要折射率连续变化,也没有超薄层,故其制造工艺难度相对褶皱设计较低。
下面用膜系结构式来描述上述膜系结构。
设有高、低折射率两种薄膜材料,在设计波长λ0处的折射率分别为nH和nL,利用共镀技术,可使折射率在nmax和nmin之间变化(其中:nmax≤nH,nmin≥nL)。不妨令nmin=nL,这不影响设计效果,却能降低膜系在工艺中实现的难度。
为了清晰描述膜系,先进行以下约定:下述的每一符号均代表一种材料在设计波长λ0处的1个光学厚度,即λ0/4。
L:折射率为nL的低折射率材料;
Mi(i=1,2,…,k):一组单层内折射率固定、而层间折射率递增的混合材料,折射率由nL经k步单调增大到nmax;
Nj(j=1,2,…,k):与 Mi类似的另一组混合材料,折射率由nmax经k步单调减小到nL;
B:折射率为nmax的混合材料。
将上述材料按以下方式组合:
其中:i=2,…,k;j=1,2,…,k-1。使B和L的组合重复s次,即可形成阻带中心在λ0处的陷波干涉效果,其光谱指标令人满意,无须额外优化。
1.2 光学特性计算
上述膜系的光学特性可通过传统的薄膜特征矩阵[17]进行计算。光学薄膜的特征矩阵如下:

式中:u为膜层总数;δj为各膜层的位相厚度;ηj为各膜层的修正导纳;ηs为基片的修正导纳。
设光线以θ0角度入射,当θ0不为0时,需分别考虑p偏振和s偏振,对入射介质导纳、各膜层导纳和基片导纳,按相应折射角进行修正。不妨设Y0为入射介质导纳,Yj为各膜层导纳,Ys为基片导纳,则它们的修正导纳η0、ηj和ηs分别为:

式(2)中的位相厚度δj可通过下式得到:

式中:dj为第j层薄膜的物理厚度。
式(4)~式(6)中的折射角θj和θs可根据菲涅耳公式转换为与入射角θ0之间的关系:

上述计算过程可借助计算机实现。获得薄膜特征矩阵后,根据式(9)~式(11)可得到薄膜的反射率(R)、透射率(T)和截止深度(OD)等光学特性参数:

下文中各结果均是基于上述公式得到的。
1.3 膜系典型示例
令设计波长λ0=532nm,Mi、Nj为高、低折射率材料(Ta2O5和SiO2)的混合材料,并设定以下参数:
(1)最大折射率nmax=1.6,分离步数k=30,堆叠数s=30;
(2)Mi以正弦规律y=sinx x⊆[0,π/2]进行变化;Nj以正弦规律y=sinx x⊆[π/2,π]进行变化。
理论计算的光谱曲线如图3所示。
2 各参数对光谱性能的影响
下面以1.3中给出的典型示例为基础,分析计算各参数对陷波滤光片光谱性能的影响。由于远离阻带的左右通带区域,其光谱性能受各参数变化的影响不大,以下图示中只给出了阻带中心附近区域的变化情况。
2.1 分离步数k的影响
其他参数保持不变,改变分离步数k,分别取10、20和30,其光谱指标理论值如表1所示,相应光谱曲线如图4所示。在阻带附近,随着k值的增加,通带波纹由21.7%减小到4.4%,截止背景由OD 2.3增加到OD 4.0,而阻带宽度变化不大。
表1 不同k值下光谱指标的理论值Tab.1 The theoretical values of the spectral parameter under different

表1 不同k值下光谱指标的理论值Tab.1 The theoretical values of the spectral parameter under different
k 阻带宽度/nm 通带最大波纹/%阻带中心背景10 29.8 21.7 OD 2.320 27.9 11.5 OD 3.230 26.8 4.4 OD 4.0

图4 光谱随k的变化趋势Fig.4 The spectral changes with k
2.2 堆叠数s的影响
其他参数保持不变,取分离步数k=10,改变堆叠数s,分别取10、20和30,其光谱指标理论值如表2所示,相应光谱曲线如图5所示。在阻带附近,随着堆叠数s的增加,通带波纹由4.2%增大到21.7%,截止背景由 OD 1.0增加到OD 2.3,而阻带宽度变化不大。

表2 不同s值下光谱指标的理论值Tab.2 The theoretical values of the spectral parameter under different s
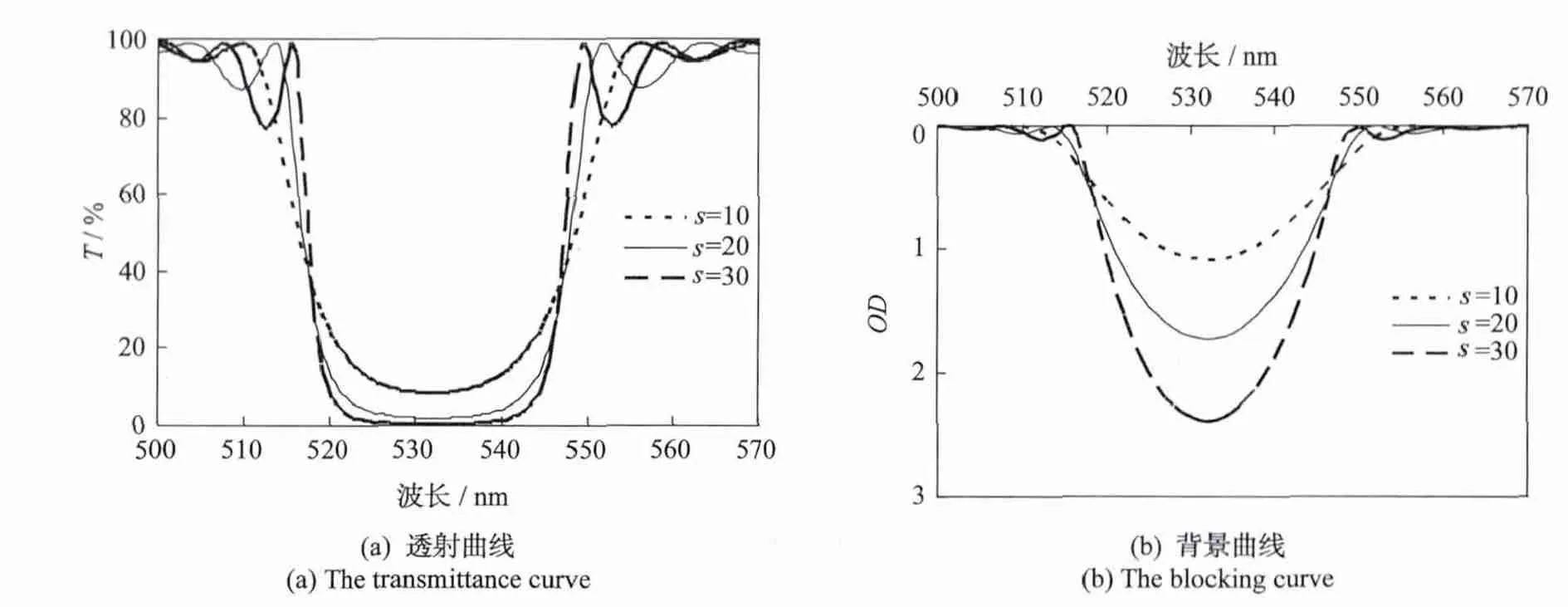
图5 光谱随s的变化趋势Fig.5 The spectral changes with s
2.3 最大折射率nmax的影响
其他参数保持不变,改变最大折射率nmax,分别取1.6、1.8和2.0。其光谱指标理论值如表3所示,相应光谱曲线如图6所示。随着nmax取值的增大,其与最小折射率nL之间的差值也随之变大,相应的阻带宽度由26.8nm加宽到98.1nm,截止背景由OD 4.0加深到OD 17.5,而通带波纹也由4.4%增大到20.8%。

表3 不同nmax值下光谱指标的理论值Tab.3 The theoretical values of the spectral parameter under different nmax
2.4 折射率分离方式的影响
设定如下两种分离方式:
(1)分离方式 A(简称“方式 A”):Mi以正弦规律y=sin x x⊆[0,π/2]进行变化,Nj以正弦规律y=sinx x⊆[π/2,π]进行变化;
(2)分离方式B(简称“方式B”):Mi以线性规律增大,Nj以线性规律减小。
其他参数保持不变,分别以分离步数k=10、20和30,比较A、B两种分离方式的区别。其光谱指标理论值如表4所示,相应光谱曲线如图7~图9所示。
透射特性:当分离步数k=10时,在阻带附近两侧的通带区内都存在较大波纹,方式A的波纹达到21.7%,方式B的波纹仅为11.6%;然而随着k值的增加,两种分离方式的波纹都逐渐减小,当k=30时,方式A的波纹为4.4%,方式B的波纹为4.1%,二者结果接近;
表4 不同分离方法及值下光谱指标的理论值Tab.4 The theoretical values of the spectral parameter under different separation and

表4 不同分离方法及值下光谱指标的理论值Tab.4 The theoretical values of the spectral parameter under different separation and
k=10方式A 方式B k=20方式A 方式B k=30方式A 方式B阻带宽度/nm 29.8 29.9 27.9 27.9 26.8 27.0通带最大波纹/% 21.7 11.6 11.5 6.2 4.4 4.1阻带中心背景OD 2.3 OD 2.2 OD 3.2 OD 2.9 OD 4.0 OD 3.5

图7 k=10时,两种分离方式的光谱特性对比Fig.7 The spectrum characteristics between two kinds of separation mode while k=10

图8 k=20时,两种分离方式的光谱特性对比Fig.8 The spectrum characteristics between two kinds of separation mode while k=20

图9 k=30时,两种分离方式的光谱特性对比Fig.9 The spectrum characteristics between two kinds of separation mode while k=30
截止特性:当分离步数k=10时,方式A的截止背景为OD 2.3,方式B的截止背景为OD 2.2;随着k值的增加,两种分离方式的截止背景都逐渐加深,当k=30时,方式A的截止背景达到OD 4.0,而方式B的截止背景仅为OD 3.5,方式A背景方面的优势越来越明显。
阻带宽度:两种分离方式的阻带宽度基本相同,随着k值的变化,阻带宽度变化不大。
在设计陷波滤光片时,可根据具体光谱指标,综合考虑上述各参数的影响,选取合适的参数。
3 膜系的误差模拟
在镀膜过程中,由于设备、工艺等因素,必然会出现控制误差,致使镀制出的薄膜在光谱指标上与理论设计存在偏差。误差模拟对于了解膜系的容差能力、估计成品率等方面都有重要意义。下面以1.3中给出的示例为基础,依据文献[17]中介绍的麦克劳德误差分析方法,对膜厚和折射率增加正态分布扰动,每组绘制10条曲线,分析此设计方法的容差。
3.1 厚度误差模拟
保持各层折射率不变,分别以膜厚的标准偏差为0.5%和2%进行模拟,结果如图10所示。
可以看到,膜系对厚度误差比较敏感。当膜厚偏差控制在0.5%以内时,其光谱指标令人满意;而当偏差增大到2%时,通带出现较大波纹。

图10 对膜厚的误差模拟结果Fig.10 The error simulation results of physical thickness
3.2 折射率误差模拟
保持各层膜厚不变,分别以折射率的标准偏差为1%和5%进行模拟,结果如图11所示。
可以看到,膜系对折射率误差并不敏感。当折射率偏差控制在1%以内时,其光谱接近无偏差光谱;当偏差增大到5%时,左侧通带指标依旧令人满意,右侧通带波纹由5%增大到15%左右。

图11 对折射率的误差模拟结果Fig.11 The error simulation results of refractive index
3.3 两种误差同时存在
采用共镀技术镀膜时,膜厚和折射率偏差必然同时存在。对于本示例膜系而言,若设定膜厚偏差控制在0.5%以内,折射率偏差控制在3%以内,模拟结果显示,10次随机误差模拟计算结果中,只有1次出现较大波纹,即镀制陷波滤光片可以达到90%的成功率(参见图12)。
当然,选取不同参数的膜系,其容差能力不尽相同,但通过上述误差模拟可知,这种类褶皱设计方法的膜系,对膜厚偏差更加敏感,在工艺实现时应设法保证膜厚精度,对折射率的控制精度可适当放宽。

图12 厚度标准偏差0.5%、折射率标准偏差为3%的误差模拟结果Fig.12 The error simulation results of the physical thickness standard deviation is 0.5%and the refractive index standard deviation is 3%
4 结 论
本文介绍的类褶皱陷波滤光片设计方法,薄膜层内的折射率不需连续渐变,每层为1个光学厚度,是一种规整膜系。膜系中的参数,如分离步数k、堆叠数s、最大折射率nmax和分离方式等,对光谱指标有不同的影响效果,需根据设计要求综合考虑。与折射率偏差相比,膜系对膜层物理厚度偏差更加敏感,在工艺控制中应增强对膜厚的控制精度。
[1]顾培夫.用等效折射率概念设计滤光片[J].仪器制造,1982(4):18-22.
[2]刘金城,董蕴华,高惠得,等.负滤光片膜系讨论与修改[J].哈尔滨工业大学学报,1999,31(3)59-61.
[3]张佰森,马勉军,熊玉卿,等.激光防护用负滤光片设计与镀制[C]∥真空技术与表面工程——第九届真空冶金与表面工程学术会议论文集.北京:电子工业出版社,2009:508-512.
[4]LAPPSCHIES M,GÖRTZ B,RISTAU D.Application of optical broadband monitoring to quasi-rugate filters by ion-beam sputtering[J].Applied Optics,2006,45(7):1502-1506.
[5]HENDRIX K D,HULSE C A,OCKENFUSS G J,et al.Demonstration of narrowband notch and multi-notch filters[J].SPIE,2008,7067:706702-1-706702-14.
[6]SOUTHWELL W H.Spectral response calculations of rugate filters using coupled-wave theory[J].Optical Society of America,1988,5(9):1558-1564.
[7]程鑫彬,范 滨,王占山,等.改进的傅里叶变换在Rugate滤光片设计中的应用[J].光学仪器,2008,30(5):69-74.
[8]鄢秋荣,黄 伟,张云洞.周期性渐变折射率光学薄膜的设计及光谱特性分析[J].光学仪器,2009,31(5):71-77.
[9]张俊超,方 明,邵宇川,等.Rugate filters prepared by rapidly alternating deposition[J].Chinese Physics B,2011,20(9):266-269.
[10]FAHR S,ULBRICH C,KIRCHARTZ T,et al.Rugate filter for light-trapping in solar cells[J].Optics Express,2008,16(13):9332-9343.
[11]ISHIKURA N,FUJII M,NISHIDA K,et al.Dichroic rugate filters based on birefringent porous silicon[J].Optics Express,2008,16(20):15531-15539.
[12]沈自才,沈 建,刘世杰,等.渐变折射率薄膜的分层评价探讨[J].物理学报,2007,56(3):1325-1328.
[13]张佰森,马勉军,熊玉卿,等.基于Rugate理论的负滤光片设计研究[J].真空与低温,2010,16(4):219-222,232.
[14]LAPPSCHIES M,GÖRTZ B,RISTAU D.Optical monitoring of rugate filters[J].SPIE,2005,5963:59631Z-1-59631Z-9.
[15]TIKHONRAVOV A V,TRUBETSKOV M K,AMOTCHKINA T V.Application of constrained optimization to the design of quasirugate optical coatings[J].Applied Optics,2008,47(28):5103-5109.
[16]SCHERER M.Magnetron sputter-deposition on atom layer scale[J].Vakuum in Forschung und Praxis,2009,21(4):24-30.
[17]唐晋发,顾培夫,刘 旭,等.现代光学薄膜技术[M].杭州:浙江大学出版社,2006.

