高斯光束横向光强分布的检测研究＊

刘长青，马军山，邵晓丽，陈泽军，董祥美

（上海理工大学 光电信息与计算机工程学院，上海 200093）

引 言

通常情形，激光谐振腔发出的基模辐射场，其横截面的振幅分布遵守高斯函数，故称高斯光束［1］。光斑的束腰直径或束腰半径，其束腰是指高斯光绝对平行传输的地方。高斯光束的半径是指在高斯光的横截面考察，以最大振幅处为原点，振幅下降到原点处的0.36788倍，也就是1／e倍的地方，由于高斯光关于原点对称，所以1／e的地方形成一个圆，该圆的半径，就是光斑在此横截面的半径。如果取束腰处的横截面来考察，此时的半径，即是束腰半径。沿着光斑前进，各处半径的包络线是一个双曲面，该双曲面有渐近线。高斯光束的传输特点是在远处沿传播方向成特定角度扩散，该角度即是光束的远场发散角，也就是一对渐近线的夹角，它与波长成正比，与其束腰半径成反比。

本文研究的是细光束的近轴光束，例如腔内或者腔外的激光光场都集中在光轴附近，此时高斯光束也是波动方程的解［2－6］。在测量高斯光束横截面光强分布［7－9］的试验中，为保证数据的准确性，采用了扫描法和CCD数据采集法两种不同的方法取得实验数据。

1 实验原理

从波动方程出发，均匀各向同性光学介质中有：

其中K为复数波矢，其解为：

将式（2）代入式（1）并进行缓变振幅近似，即

得：

上式的一个解为：

其中r2＝x2＋y2；参量p（z）与光束传播有关，表示相位变化的附加修正项；q（z）是一个参变量，它描述了光轴附近球面波的曲率，以及光束强度随距离r的高斯变化。将式（5）代入式（4）求得：

上式第二项不含x和y，因而对任意一点（x，y），上式都成立。比较r幂次相同的项，得到：

对式（7）积分得：

q0为积分常数。将式（9）代入式（8）式得：

积分得：

将式（9），式（11）代入式（5），可得：

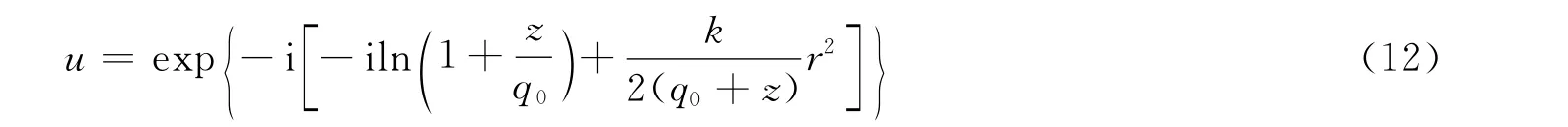
取任意常数q0为纯虚数，并用一个新的常数w0重新表示为：

由式（9），当z＝0时，q（0）＝q0＝iπw20／λ，将发现对虚数q0的选择可得出有物理意义的光波。这些波的能量密度约束在光轴附近。利用式（13）的代换，分别讨论式（12）中两个因子。第二个因子变为：

若定义如下参量：

则（14）式变为：

对第一个因子的计算如下：

最后得出：

在直角坐标系下，其光强分布［10］可表示为

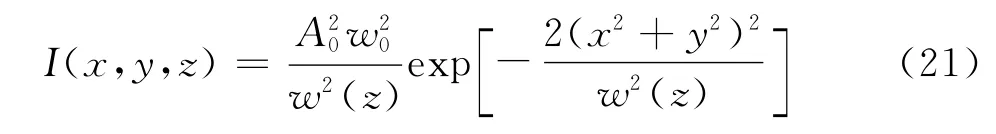
式中，A0为振幅常数，w0为高斯光束的束腰半径。图1为基模高斯光束的光强分布图。

2 实验装置

激光可以会聚成非常小的一点，所以可作为一个接近于理想的点光源来产生球面波，激光又具有高度的相干性，但易受空中的灰尘、光学元件或激光本身产生的一些散射光的干扰，因此要在会聚的点上放一个小孔，使杂散光不能通过，如图2所示。

图1 基模高斯光束的光强分布Fig.1 The intensity distribution of base mode Gauss beam

图2 针孔空间滤波器Fig.2 Pinhole spatial filter

本实验使用放大倍率为10的显微物镜对激光束进行聚焦，用直径的25μm的针孔空间滤波器［11］滤除杂散光，并调节出射激光准直［12］。

为保证数据的准确性，在采集数据的同时，同步地将用分光棱镜线性地分出的另一束光用光功率计接收，用光功率计监视激光器稳定工作，并且重复多次实验。为了确保实验数据的准确性，采用两种采集数据的实验方法：扫描法和CCD采集光斑法。

（1）扫描法

扫描法测量的实验示意图如图3所示：

图3 实验测量系统Fig.3 The experimental measurement system

首先调节激光器出射的激光水平：光路依次通过的针孔空间滤波器及准直系统的物镜由三维调节台架起，通过上下及左右的维度调节使物镜光轴与系统光轴重合，前后的维度调节使其焦平面与小孔所在平面重合；小孔用二维调节台架起，上下左右维度调节小孔与物镜焦点重合；准直镜用三维调节架架起，三维调节使准直镜中心轴与系统的光轴重合。调节激光准直后，在垂直于光束的平面内扫描光斑。

扫描装置控制：根据光斑的尺寸（直径约10mm）预设程序参数，控制扫描探头的移动范围，同时预设信号采集卡的采样行数和每行采样点数（为保证精度设为150×150个点）。

信号采集说明：扫描探头是由光敏二极管、7650芯片、电阻、电容等组成的将光强度信号转换为放大的电信号的电路，然后电信号连接到信号采集卡，由信号采集卡的控制程序记录并保存电信号强度的文本数据。

扫描探头说明：用光敏二极管作为信号采集的探头，为提高分辨率在二极管的光敏面前放一个小孔（直径100μm），扫描探头的电路设计中有滤除低频噪声干扰功能，避免频率不同的杂散光噪声干扰目标光斑信息的采集。

开始扫描光斑之前，先由光功率计检测激光器的功率是否稳定，避免因为激光器功率不稳定带来的误差。在实验中光功率计显示激光器平稳时段的功率，并进行采样记录数据。

采集数据：首先确保扫描探头的运动轨迹平面要与光轴垂直，用扫描探头扫描整个光斑，扫描范围要略大于光斑尺寸，确保能扫描到整个光斑，通过光电转换电路将光强度转换为电压信号并由程序记录文本数据，然后将文本数据导入到Mathematica图像处理程序中，得到光斑横截面光强分布等高线，如图4所示。同时得到光束横截面的强度分布与理论的高斯分布曲线拟合对比，如图5所示。

（2）CCD采集光斑法

用CCD采集光斑图样，调节CCD感光平面与光轴垂直，调节光斑恰好在有效感光面范围内，用中性密度片调节光强度到适中，多次重复采集数据，最后选取最理想的图样数据，用图像处理软件转换为灰度图，如图6所示。

用图像处理程序读取通过光斑中心的一条线上的光强数据，并与理论高斯分布曲线拟合画成直角坐标系图，如图7所示。

综合图5和图7可以看出，实验检测的曲线与理论高斯分布曲线吻合，在光束的其它位置多次重复上述两种采集数据的步骤，得到同样的结果。

图4 光强分布“等高线”图Fig.4 The contour lines of intensity distribution

图5 扫描法得到的光强分布与高斯分布曲线拟合图Fig.5 The fitting between Gauss distribution and intensity distribution by the method of micropore scanning

图6 光束横截面光斑的灰度图Fig.6 The grey－scale picture of transverse of Gauss beam

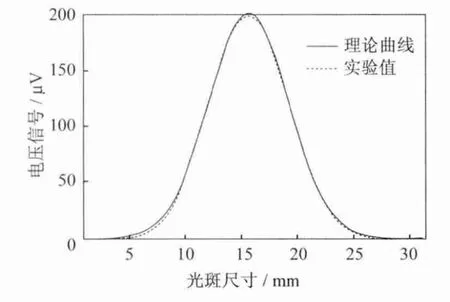
图7 CCD法测得光强分布与高斯分布曲线拟合图Fig.7 The fitting between Gauss distribution and intensity distribution by the method of CCD

3 结 论

激光谐振腔发出的基模辐射场，其横截面的振幅分布遵守高斯函数，故称高斯光束，而且理论上从波动方程可以推出高斯光束的解。实验中微米级的小孔以很小的步距对光斑进行精确二维扫描，再经低噪声的I／V转换电路和电压放大电路处理，将取样信号送入计算机中处理，可以准确地复原光斑的能量分布。CCD采样法，可通过计算机处理直接分析取样光斑的强度分布，实验检测光强分布与理论高斯光束光强分布吻合。理论和实验都证实了这两种方法的精确性。

［1］王青圃，张行愚，刘泽金，等.激光原理［M］.济南：山东大学出版社，2003：155－158.

［2］李文成，谷晋骐，王涌萍.激光光斑及束腰光斑尺寸的测量研究［J］.应用光学，2002，23（3）：30－33.

［3］李 强，雷 訇，左铁钏.大功率激光光束光斑参数的测量［J］.光电子 激光，2000，11（5）：473－475.

［4］蔡伯荣，魏光荣.激光器件［M］.长沙：湖南科学技术出版社，1981：38－39.

［5］康小平，何 仲.激光光束质量评价概论［M］.上海：上海科学技术文献出版社，2007：19－21.

［6］卡拉德 T.激光演示实验［M］.北京：人民教育出版社，1980：65－68.

［7］范志刚，左保军，张爱红.光电测试技术［M］.北京：电子工业出版社，2008：148－158.

［8］刘国平，周 斌，刘秉琦.激光主动探测系统二维均匀扫描设计［J］.光学仪器，2011，33（5）：90－93.

［9］盛 伟，李季平，陈加林，等.散斑干涉条纹测量系统设计［J］.光学仪器，2013，35（3）：58－62.