基于遗传优化KPCA的齿轮泵状态识别研究

王涛，李艾华，蔡艳平，王旭平，姚良

(第二炮兵工程大学机电工程系，陕西西安710025)

液压泵是液压系统的心脏，其性能的好坏将直接影响液压系统乃至整个机械设备的正常工作，对它进行状态监测和故障诊断至关重要。目前，国内外学者对液压泵故障诊断进行了不同角度的研究［1-3］。齿轮泵是较为常用的液压泵种类之一，据不完全统计，齿轮泵在液压泵中约占78.2%［4］，而且其使用领域还在不断扩大。因此，研究齿轮泵的故障模式识别方法具有重要的现实意义。

核主元分析(Kernel Principal Component Analysis，KPCA)是SCHÖLKOPF 等在研究支持向量机分类算法时提出的［5］，这一方法保留了主元分析(Principal Component Analysis，PCA)的优点，并具有处理非线性问题的能力，目前已经在机械故障诊断中得到了成功应用［6］。齿轮泵在运行中故障的发生往往会导致非线性行为，因此KPCA 为齿轮泵故障诊断识别提供了一种可能的途径。核函数是KPCA 的关键，它不仅直接影响特征空间样本的可分性，而且影响后续分类精度。但是，如何根据具体问题选择最优核函数及其参数，目前仍缺乏有力的理论依据。在应用KPCA 前，核函数一般人为选定，而核参数通常由人工反复试验或采取交叉验证法确定。人工方式耗时多、效率低，交叉验证法计算量大，且上述两种方式所选核参数也不一定最优，因此，对核参数优选问题进行研究具有重要意义。文献［7］基于矩阵相似度量优化径向基核函数的宽度参数，减小了计算量且取得了较好的分类效果;文献［8］通过最小化均方预测误差选择合适的核函数和参数，提高了模型的泛化能力;文献［9 -10］分别采用文化算法和粒子群算法对核参数进行优化选择，取得了较好的分类效果。目前常用的核函数有线性核函数、多项式核函数、径向基核函数和sigmoid 核函数4 种。其中，径向基核函数具有某些良好的性态，并且在缺少过程先验知识时，往往表现出比其他核函数优良的性能，因此，作者选择径向基核函数作为核函数，研究其宽度参数w 的优化问题。遗传算法是一种全局并行寻优方法，近年来，在函数优化、自动控制、机器学习、人工生命等领域已得到了广泛应用。作者利用一种改进的自适应遗传算法优选径向基核参数w，并将优化KPCA 算法应用于齿轮泵故障状态识别。

1 遗传优化核主元分析法

1.1 改进的自适应遗传算法

针对传统遗传算法中交叉概率pc和变异概率pm需要反复实验确定，且很难找到适应于每个解的最佳值问题，SRINVIVAS 等［11］提出一种自适应遗传算法(Adaptive GA，AGA)，其中pc和pm能够随适应度自动改变。自适应遗传算法在保持群体多样性的同时，还能保证遗传算法的收敛性。在自适应遗传算法中，pc和pm按如下公式进行自适应调整:

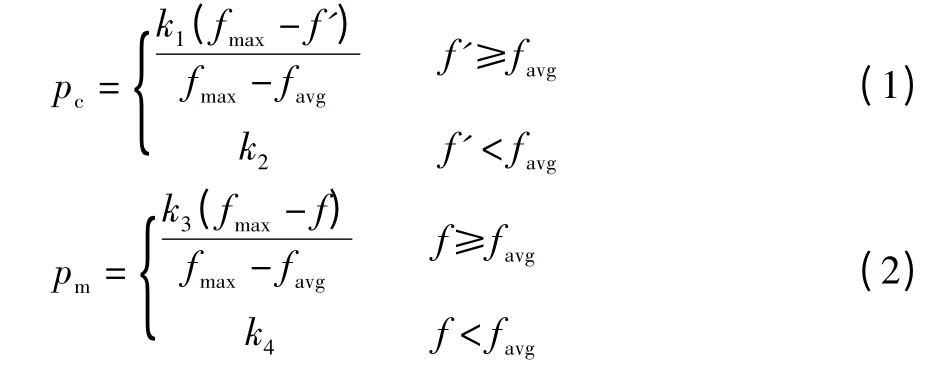
式中:fmax为群体中最大的适应度值;favg为每代群体的平均适应度值;f'为要交叉的两个个体中较大的适应度值;f 为变异个体的适应度值。只要设定k1，k2，k3，k4取(0，1)区间的值，pc和pm就可以自适应地进行调整。自适应遗传算法调整交叉概率pc和变异概率pm的原则是:当适应度值低于平均适应度值时，说明该个体是性能不好的个体，对它就采用较大的交叉和变异率;如果适应度值高于平均适应度值，说明该个体性能优良，对它就根据其适应度值取相应的交叉和变异率。可以看出，当适应度值越接近最大适应度值时，交叉和变异率的值就越小;当等于最大适应度值时，交叉和变异率的值为零。这种调整方式对群体进化后期比较合适，但对进化初期不利。这是因为在进化后期，群体中每个个体基本上表现出较优的性能，此时不宜对个体进行较大的变化，以免破坏个体的优良性能结构;而在初期阶段，群体中较优的个体几乎处于一种不变的状态，但此时的优良个体并不能保证就是问题的全局最优解。为此，对该方法进一步改进［12］，使群体中最大适应度值的个体的交叉和变异率不为零，分别提高到pc2和pm2，这就相应地提高了群体中表现优良的个体的交叉和变异率，使得它们不会处于一种近似停滞不前的状态。经过上述改进，pc和pm的计算表达式如下:

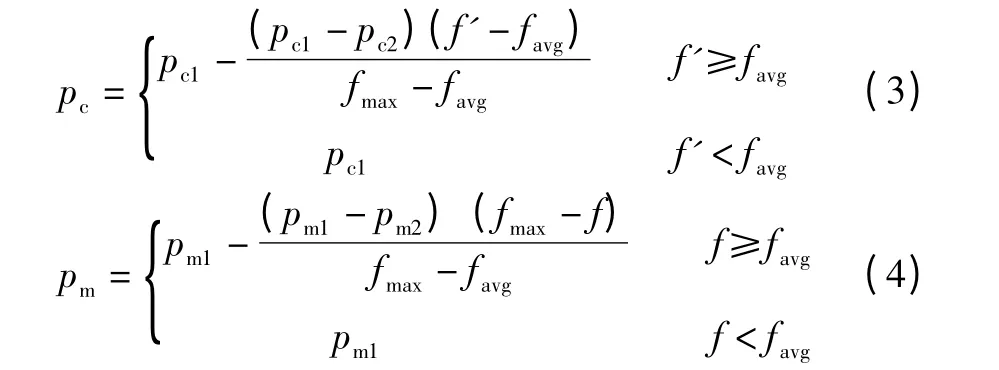
式中:pc1取0.7 ～0.9，pc2取0.5 ～0.6，pm1取0.1 ～0.2，pm2取0.005 ～0.06。

正是自适应遗传算法具有上述优势，作者采用改进自适应遗传算法优化核参数w。在应用中，式(3)和式(4)中的参数pc1、pc2、pm1和pm2均取各自范围内的最大值。

1.2 遗传优化核参数的步骤

为了采用自适应遗传算法优化核参数w，首先需要确定评估个体参数的适应度准则。由于KPCA 通常被用于提取非线性特征，而特征提取的最终目的是为了增强类别可分性，因此作者以类别可分性作为适应度准则。在分类问题中，通常通过类间距Sb和类内距Sw两个散度矩阵测度类别间的可分性。Sb的值越大，说明类与类之间的差别越大，分类效果越好;Sw的值越小，说明类内的差别越小，样本聚类的效果也就越好。因此，可将适应度函数定义为如下表达式:

其中:Sb和Sw分别是类间和类内散度矩阵，FJ是可分性测度。

可以通过式(6)—(8)在高维特征空间计算Sb和Sw:

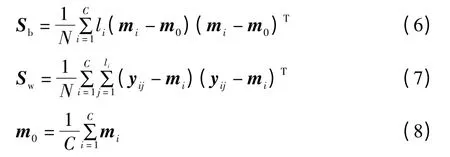
其中:N 是训练样本数量;C 是类别数量;li是第i类中训练样本数量;yij是第i 类中第j 个样本;mi是第i 类中训练样本的均值向量;m0是所有类别训练样本的均值向量。FJ越大，各类间的可分性越好。

按照上述优化准则，作者所提基于改进自适应遗传算法优化核参数w 的步骤如下:

步骤1，通过式(6)、(7)分别计算类内矩Sb和类间距Sw散度矩阵;

步骤2，通过式(5)构造适应度函数，并将该函数作为遗传算法优化的目标函数;

步骤3，设定核参数w 的取值范围，以及种群规模M、迭代次数T、交叉概率pc1和pc2、变异概率pm1和pm2;

步骤4，随机产生初始群体p0，计算个体的适应度值f0i和种群的整体适应度值;

步骤5，判断迭代次数t 是否达到终止条件。如果t ＜T，继续下列各步，否则将当前解作为最优输出解，算法终止;

步骤6，产生新个体。按交叉概率pc1和pc2采用算术交叉和轮盘赌选择方法产生新个体，并将交叉后所产生的新个体及父代中的个体按变异概率pm1和pm2进行非均匀一致变异，得到一些新个体;

步骤7，评价新个体。计算个体适应度fi和新种群的整体适应度F1，并选择新的种群P1;

步骤8，令t=t +1，P0= P1，F0= F1，返回步骤5。

2 齿轮泵故障诊断实例及分析

作者以某液压实验台上的CB-KP63 型高压齿轮泵为例，为了研究齿轮泵在不同故障下各监测参数的变化情况，在实验中设置了轴承故障、侧板磨损、齿轮磨损等3 类故障。对于包括正常在内的齿轮泵的4种常见工作状态，分别测取了从空载直到出口压力为20 MPa 时的泵壳振动加速度信号，压力上升的间隔为1 MPa，每种情况各测取了20 组数据，共80 组数据。

2.1 齿轮泵状态信号预处理

每种工作状态各取前10 组数据，共40 组构成训练样本集，剩余40 组构成测试样本集。首先用3 层小波包分解原始采样数据，小波基为db5，每个采样数据被分解为8 个频带，计算各频带能量特征并进行归一化处理，然后以8 个频带的归一化能量构造8 维特征向量。齿轮泵4 种运行状态典型的归一化频带能量特征如表1所示。

表1 齿轮泵4 种运行状态的特征组成

2.2 径向基核函数参数优化

针对训练样本集采用改进自适应遗传算法对核参数w 进行优化，其中参数设置如表2所示，进化过程及迭代结果如图1所示。

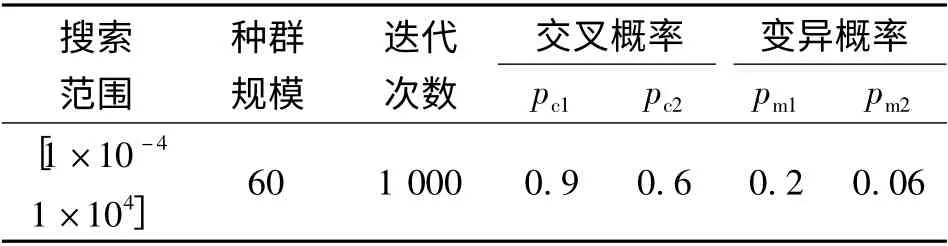
表2 改进自适应遗传算法参数设置表

从图1 可以看出:在解的优化过程中，个体的适应度最大值和平均值虽然有上下波动的情况，但总的来说呈现一种上升的趋势，达到一定进化代数后，趋于平稳，最终搜索到了问题的最优解。对于上述数据集，最优核参数w 的值为0.311 1，对应的最佳适应度值为4.826 2。该最优核参数w 的值作为齿轮泵故障特征集进行核主元分析时的参数设置依据。

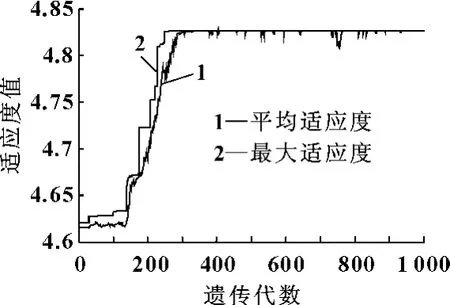
图1 优化过程及结果

2.3 齿轮泵故障模式分类

以上述优化得到的核参数w 值为依据，设置w=0.3，对齿轮泵40 组测试数据集分别进行PCA 和KPCA 分析，并对分析结果进行归一化处理。用这两种方法计算得到的前3 个主元贡献率以及累积贡献率如表3所示，分析结果如图2 和图3所示。

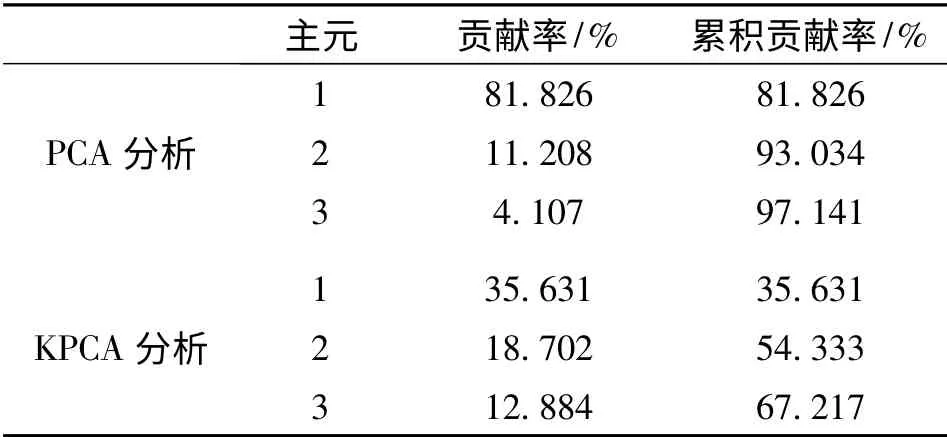
表3 PCA 和KPCA 主元贡献率比较

由图2 可知:线性主元分析对于齿轮泵的状态模式难以有效区分，虽然在1-2 主元投影图上各状态特征点基本可分，但类间距非常小，区分不明显，且类内距很大，聚类效果很差;在1-3 主元投影图和2-3主元投影图上，识别效果进一步变差，正常状态和侧板磨损、轴承磨损以及齿轮磨损的特征样本混杂在一起，难以区分，所得主元投影不能很好地区分以上4种运行状态。此外，从表3 可知:传统的主元分析降维效果非常明显，第一个主元携带的特征变异信息就达到了81.826%，前2 个主元的累积贡献率达到了93.034%。但即使这样，采用PCA 进行故障模式分类的效果仍不理想，究其原因是因为齿轮泵从正常状态到轴承磨损、齿轮磨损、侧板磨损，振动发生了非线性行为，线性主元分析方法已不再适用。

图2 PCA 对齿轮泵状态识别结果

图3 KPCA 对齿轮泵状态识别结果

反观KPCA 的分析结果，虽然从表3 看到它的前3 个非线性主元的累积贡献率仅为67.217%，远小于PCA。但从图3 可知:无论在1-2 核主元投影图上，还是1-3 核主元投影图上，均能有效区分出齿轮泵的4 种状态，且各类的聚类效果明显增强，不同类之间散布也较远;虽然在2-3 核主元投影图上，正常状态与轴承磨损的特征样本有少数几个点混杂在一起，但这并不影响总体的识别效果。从以上分析可以看出:采用KPCA 分析的识别效果明显优于采用PCA 分析的效果，表明了KPCA 在非线性故障分离中具有强大的优势。

3 结束语

提出一种基于改进自适应遗传算法的核参数优化方法。该方法以类别之间的可分性为准则，建立遗传优化目标函数，克服了传统核参数设置存在盲目性、效率低的问题。将该方法应用到齿轮泵的模式识别中，结果表明:与PCA 方法相比，作者所提方法不仅能够有效降低原始特征向量的维数，而且聚类效果明显，通过各核主元之间的投影能很好地将齿轮泵的正常状态、齿轮磨损、侧板磨损、轴承故障4 种状态分离出来。

【1】杜巧连，张克华.基于自身振动信号的液压泵状态监测及故障诊断［J］.农业工程学报，2007，23(4):120 -123.

【2】ZHAO Zhen，JIA Mingxing，WANG Fuli，et al.Intermittent Chaos and Sliding Window Symbol Sequence Statisticsbased Early Fault Diagnosis for Hydraulic Pump on Hydraulic Tube Tester［J］.Mechanical Systems and Signal Processing，2009，23(5):1573 -1585.

【3】HANCOCK K M，ZHANG Q.A Hybrid Approach to Hydraulic Vane Pump Condition Monitoring and Fault Detection［J］.Transactions of the ASABE，2006，49(4):1203 -1211.

【4】俞云飞.液压泵的发展展望［J］.液压气动与密封，2002(1):2 -6.

【5】SCHÖLKOPF B，SMOLA A，MÜLLER K R.Nonlinear Component Analysis as a Kernel Eigenvalue Problem［J］.Neural Computation，1998，10(5):1299 -1319.

【6】蒋静，李志农，易小兵.基于Volterra 级数和KPCA 的旋转机械故障诊断方法研究［J］.噪声与振动控制，2011(1):119 -122.

【7】王新峰，邱静，刘冠军.核主元分析中核函数参数选优方法研究［J］.振动、测试与诊断，2007，27(1):62 -64.

【8】毕小龙，王洪跃，司风琪，等.基于核主元分析的传感器故障检测［J］.动力工程，2007，27(4):555 -559.

【9】黄海燕，柳桂国，顾幸生.基于文化算法的KPCA 特征提取方法［J］.华东理工大学学报，2008，34(2):256 -260.

【10】魏秀业，潘宏侠，王福杰.基于粒子群优化的核主元分析特征的提取技术［J］.振动、测试与诊断，2009，29(2):162 -166.

【11】SRINIVAS M，PATNAIK L M.Adaptive Probabilities of Crossover and Mutation in Genetic Algorithms［J］.IEEE Transactions on Systems，Man and Cybernetics，1994，24(4):656 -667.

【12】段玉倩，贺家李.遗传算法及其改进［J］.电力系统及其自动化学报，1998，10(1):39 -51.