两体量子模型的代数动力学方法求解

张新琴，夏秀文，罗小兵



两体量子模型的代数动力学方法求解

*张新琴，夏秀文，罗小兵

（井冈山大学数理学院，江西，吉安 343009）

引入广义坐标和广义动量，将非线性自洽两体量子模型表述为经典不含时哈密顿系统并实现了去约束经典哈密顿量的正则化。量子系统的整体规范不变性，体现在去约束经典哈密顿量和哈密顿动力学关系的不变性中。利用代数动力学方法求解经典哈密顿方程，得到了两体量子系统的六阶近似分析解。

非线性自洽量子系统；正则变换；哈密顿量；代数动力学

对于一个非线性自洽量子系统，利用波函数来描述量子态，量子态演化满足薛定谔方程；假定量子系统具有整体规范变换不变性，物理上很多系统都满足这种对称性，则无量纲化非线性薛定谔方程为：

其中，量子系统的哈密顿量(*,)不含时，称该系统为非线性自洽量子系统。如此，量子系统的行为就归结为求解非线性薛定谔方程问题；一般而言，非线性薛定谔方程难以求得精确解，因而对薛定谔方程（1）的分析广泛采用数值计算方法；目前常采用数值算法主要有Runge-Kutta算法和辛几何算法以及代数动力学方法[1]。

基于代数动力学方法求解常微分方程的思想，王顺金等[2]发展了偏微分方程的数值求解算法，即泛函空间的代数动力学算法，并将其应用于线性和非线性薛定谔方程的求解。这种方法直接从分析薛定谔方程入手，通过引进泛函偏微分算子和时间演化算子，将方程（1）改写为泛函偏微分方程，实现数值求解。代数动力学方法的正确性已经被印证，其数值求解的精确度也普遍优于其它数值算法。

而对于具有经典哈密顿量形式的量子系统，利用代数动力学方法可以很方便地判断系统是否有精确解，在一般情况下可以给出系统演化的任意阶精度解析解。这样，就可以从量子系统的经典化哈密顿量和正则方程出发，寻求量子系统的精确解或近似解析解。本文以二体模型为例，分析求解了该非线性自洽量子系统六阶近似解。

1 两体模型的经典正则化

以两体模型为例[4]，=2，假定非线性薛定谔方程满足：

这个模型被用来描述双势阱中的隧穿现象，参量、分别描述了原子间的相互作用强度和两能级的耦合强度，参数为两势阱能级之差；若参数不随时间变化，则哈密顿量不显含时间，该系统为非线性自洽量子系统。

很容易验证，该系统可以被表述为经典哈密顿系统，经典正则化哈密顿量为：

H=-(1+2+2+1)/2-(1+1-2+2)/2+(1+1-2+2)2/4 (3a)

其中+=*(=1,2)；对波函数做几率和相位变换：

经典化哈密顿量被表述为：

可见经典哈密顿量中与相位有关的变量自然地表述为相位差的形式，因而可以对波函数做规范变换分离出整体相位：

其中()=-2。记=1，=1-2，则经典化哈密顿量（3b）可以表示为：

这样就得到了满足正则方程的用正则变量表示的经典化哈密顿量；哈密顿量（3c）满足哈密顿正则方程：

如此，就完成了把一个非线性自洽量子系统经典化为一个经典自洽哈密顿系统；量子系统规范变换后的解归结为求解（6）式哈密顿正则方程，大大降低了量子系统的求解难度。利用代数动力学方法，可以得出（6）式的泰勒级数解，对于某些特殊系统，可以给出系统的精确解；对于一般系统，可以给出任意精度截断的近似解析解。

将用分量整体相位后的波函数（5）式代入非线性薛定谔方程（2）式，可以得到整体相位的满足：

值得注意的是，（7）式中量子系统经典化哈密顿量具有规范变换不变性H(+,)= H(+,) (=1,2)，但哈密顿正则方程（6）式不具有规范变换不变性。由于(+,) (=1,2)可以由（3a）式确定，因而（7）式实际为含有正则变量、的微分方程，只要对（7）式积分就可以得出整体相位。

2 代数动力学方法求解哈密顿正则方程

为了求解哈密顿正则方程（6），做变量代换：

则式（6）可以表示为：

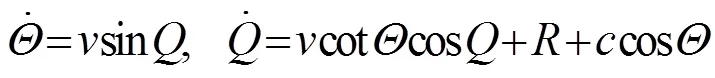
微分方程（9a）转化为偏微分方程：

其中，0、0为微分方程的初始条件。由此可得方程（9b）的解为：

其中，0=0(0,0)由量子系统的初始状态确定；可得系统的时间演化算子为：

时间演化算符的六阶近似[1]为：

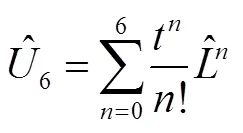
若取量子系统的初始条件为0=0.5，0=0，在函数的收敛区域内六阶近似解为：

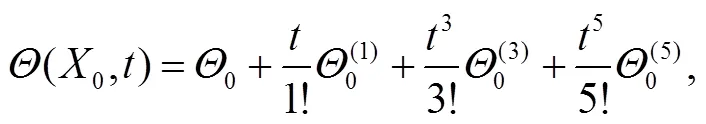
其中各参数如下：

由此可得波函数的六阶解析解为：

其中，、由（13）式给出。

3 两体系统的整体相位和几何相位

将波函数代入（7）式，可得整体相位满足：

其中，

表征了该系统的几何相位；

表征了该系统的动力学相位。

由于被积函数的表达式非常复杂，很难得出整体相位的解析解。取的初始值为0，和的初始值分别为/2和0，则可以通过代数动力学方法给出任意阶近似解。引入时间平移微分算符为：

可得在收敛区间内整体相位的六阶近似解为：

其中各参数如下：

利用代数动力学方法可得几何相位1(,)在收敛区间内的六阶近似解为：

其中各参数如下：

4 总结

引入恰当的广义坐标和广义动量，可以把量子系统严格地表述为经典哈密顿系统，这对分析和求解量子系统非常有意义。对于一个非线性自洽量子系统，通过引入广义动量波函数几率和广义坐标波函数相位，量子系统被转化为一个经典哈密顿系统，且(p,q)(=1，2，…，)为经典化后的不含时含约束哈密顿量的正则变量；由于波函数满足归一化条件，经典含约束哈密顿量中与相位有关的变量可以自然地表述为相位差变量，实现了去约束经典哈密顿量的正则化，独立变量(,=-q) (=1,2，…,-1)为去约束哈密顿正则变量；去约束哈密顿量和哈密顿正则关系具有整体规范变换不变性。

从非线性自洽量子系统可以被转化为经典哈密顿系统和去约束经典哈密顿量正则方程出发，利用代数动力学解法，实现了量子系统的任意精度分析求解，并利用该方法得到了两体模型的六阶近似解析解。

[1] 王顺金,张华.物理计算的保真与代数动力学算法-II.代数动力学算法与其他算法计算结果的比较[J].中国科学(G辑),2006,36(1):14-37.

[2] 王顺金,张华.物理计算的保真与代数动力学算法-IV.偏微分演化方程的代数动力学解法与算法[J].中国科学(G辑),2008,38(2):178-193.

[3] Steven Weinberg.Testing quantum mechanics [J]. Annals of Physics,1989,194(2):336-386.

[4] Liu Jie, Wu Biao, Niu Qian. Nonlinear evolution of quantum states in the adiabatic regime [J]. Physical Review Letters, 2003,90(17):170404-1~170404-4.

[5] Wu Biao, Liu Jie, Niu Qian. Geometric phase for adiabatic evolutions of general quantum states [J]. Physical Review Letters, 2005,94:140402-1~140402-4.

[6] 吴飙,刘杰.绝热演化中一般量子态的几何相位[J].研究快讯,2005,34:883-886.

[7] Liu J, Fu L B.Berry phase in nonlinear systems [J]. Physical Review A, 2010,81: 52112-1-052112-5.

[8] 王顺金,张华.物理计算的保真与代数动力学算法-I.动力学系统的代数动力学解法与代数动力学算法[J].中国科学(G辑),2005,35(6):573-608.

USING ALGEBRAIC DYNAMICS METHOD TO SOLUTE TWO-MODE QUANTUM SYSTEM

*ZHANG Xin-qin, XIA Xiu-wen, LUO Xiao-bing

(School of Mathematics and Physics, Jinggangshan University, Ji’an, Jiangxi 343009, China)

As it well known, quantum system can be translated to classic Hamilton system strictly by using generalized coordinate and generalized momentum. Furthermore, we deal with a nonlinear self-consistent two-mode quantum system which shows that the Schrodinger equations can be described as classic Hamilton equations. Furthermore, the classic Hamiltonian and the Hamilton equations kept unchanged during gauge transformation. Taken advantage of algebraic dynamics, the quantum system can be solved analytically in 6thorder.

nonlinear self-consistent quantum system; canonical transformation; Hamiltonian; algebraic dynamics

1674-8085(2013)02-0028-04

O413.1

A

10.3969/j.issn.1674-8085.2013.02.006

2012-09-22；

2013-02-06

国家自然科学基金项目(10965001)

*张新琴(1978-)，女，江西余江人，讲师，硕士，主要从事凝聚态物理研究(Email: jgsuzxq@163.com);

夏秀文(1978-)，男，江西余江人，讲师，硕士，主要从事凝聚态物理研究(Email: jgsuxxw@126.com);

罗小兵(1978-)，男，江西遂川人，副教授，博士，主要从事玻色爱因斯坦凝聚等方面研究(Email: lxbment@yahoo.com.cn).