具有Friction边界条件的Navier-Stokes方程的两重牛顿校正算法

安 荣，王 贤

（温州大学数学与信息科学学院，浙江温州 325035）

具有Friction边界条件的Navier-Stokes方程的两重牛顿校正算法

安 荣，王 贤

（温州大学数学与信息科学学院，浙江温州 325035）

基于压力投影稳定有限元方法，给出一个求解具有Friction边界条件的Navier-Stokes方程的两重牛顿校正算法．从获得的误差估计可以看出，如果细网格尺度满足h=O（H4），那么该两重牛顿校正算法与一重稳定有限元方法具有相同的收敛阶．与有关文献相比，该算法的计算效率更高．

Navier-Stokes方程；Friction边界条件；稳定有限元方法；两重牛顿校正方法

考虑定常Navier-Stokes方程：

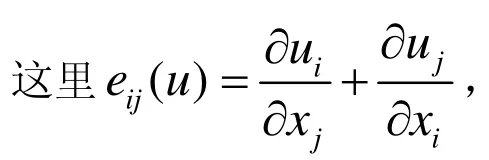
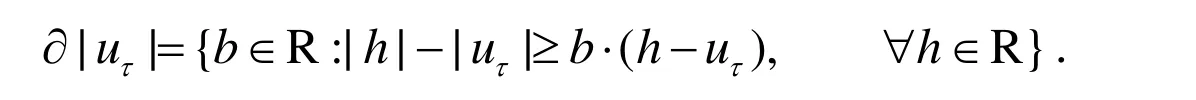
问题（1）和（2）首先是由Fujita在文献[1]中提出的，其弱变分形式为Navier-Stokes类型的第二类变分不等式问题．本文基于压力投影稳定有限元方法[1-3]，给出一个两重牛顿校正算法来求方程（1）和（2）的数值解，其求解过程可描述如下：

1）在尺度为H的粗网格上求解一个小型的Navier-Stokes型变分不等式问题；

2）在尺度为h的细网格上求解一个大型的Oseen型变分不等式问题；

3）在细网格上求解一个大型的线性化Navier-Stokes型变分不等式问题．

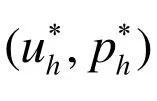
||u-uh||H1+||p-ph||L2≤c（h+H2）．

在这种情况下，如果选择h=Ο（H2），则两重Oseen算法具有最佳收敛阶．本文基于文献[5]的思想，在细网格上求解Oseen型变分不等式问题后再构造一步牛顿校正算法，得到了如下的误差估计：

从上面的估计式可以看出，若h=Ο（H4），那么两重牛顿校正算法也具有最优的收敛阶．因此，对比文献[4]中所研究的两重算法，本文所构造的两重牛顿校正算法更加节省CPU的求解时间，计算效率更高．

本文中符号c总是表示不依赖与h和H的正常数，但可能与μ和区域Ω以及u,p,f,g的范数相关．

1 具有Friction边界条件的Navier-Stokes方程

首先，引入一些常用的函数空间．

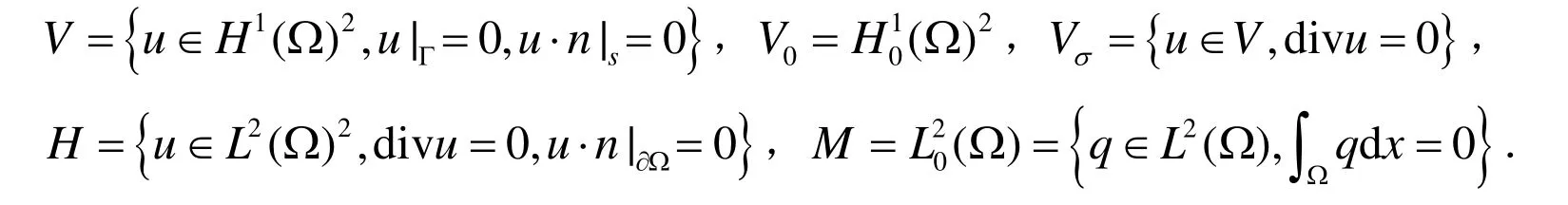
记（·,·）和||·||分别表示空间L2（Ω）和L2（Ω）2中的内积和范数，令||·||k表示空间Hk（Ω）2中通常的Sobolev范数，然后在空间V中装备内积（∇·,∇·）和范数||·||V，由Poincare不等式知，范数||∇v||与||v||1等价．

引入下面的双线性和三线性形式：

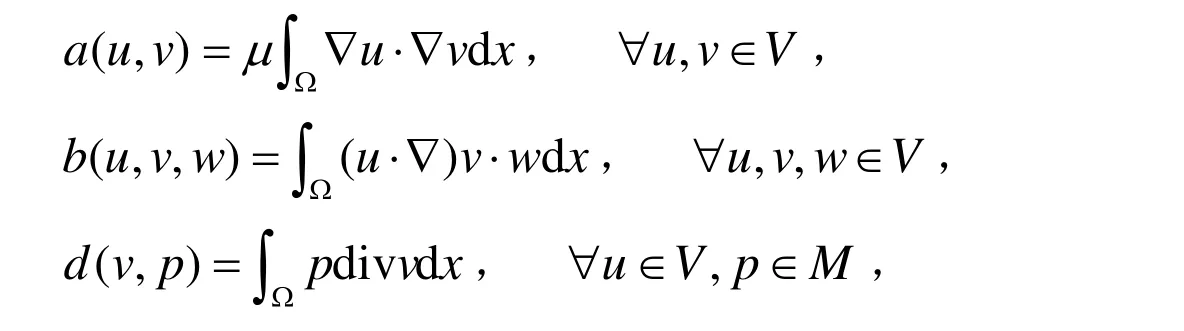
如果div u=0，那么三线性项b（·,·,·）：V×V×V →R 满足

因此三线性项b（·,·,·）：Vσ×V×V →R 具有反对称性，即

b（u,v,w）=-b（u,w,v），∀u∈Vσ,v,w∈V ．

b（u,v,w）≤N||u||V||v||V||w ||w，∀u,v,w∈V ．

给定f∈L2（Ω）2和g∈L2（Ω）并且在边界S上g≥0，则方程（1）和（2）的弱变分形式为下面Navier-Stokes型变分不等式问题，求（u,p）∈V×M 使得

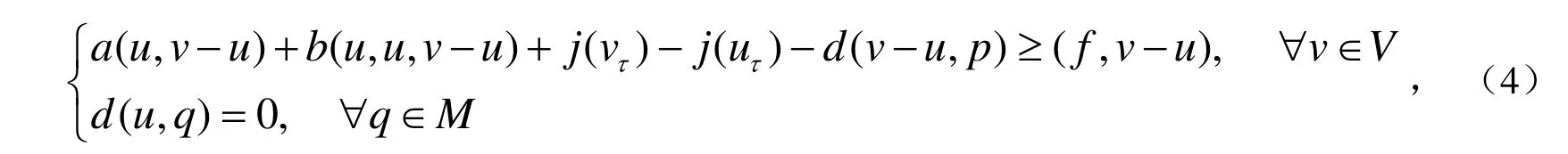
这里j（η）=∫Sg|η|d s ．由压缩映射原理和下面的唯一性条件：

文献[6]给出了方程（4）的解的存在唯一性，并且u满足下面的估计式：

这里k1＞0满足|（f,v）-j（vτ）|≤k1（||f||+||g||L2（S））||v ||V．

2 压力投影稳定有限元逼近

令Γh为区域Ω的一族正则三角形剖分，并且剖分尺度h满足0＜h＜1．定义V和M的协调有限元空间为：Vh={v∈V：v|K∈P1（K）,∀K ∈Γh}和Mh={q∈M：q|K∈P1（K）,∀K ∈Γh}，那么问题（4）的压力投影有限元逼近解（uh,ph）∈Vh×Mh满足下面的离散变分不等式问题：求（uh,ph）∈Vh×Mh使得

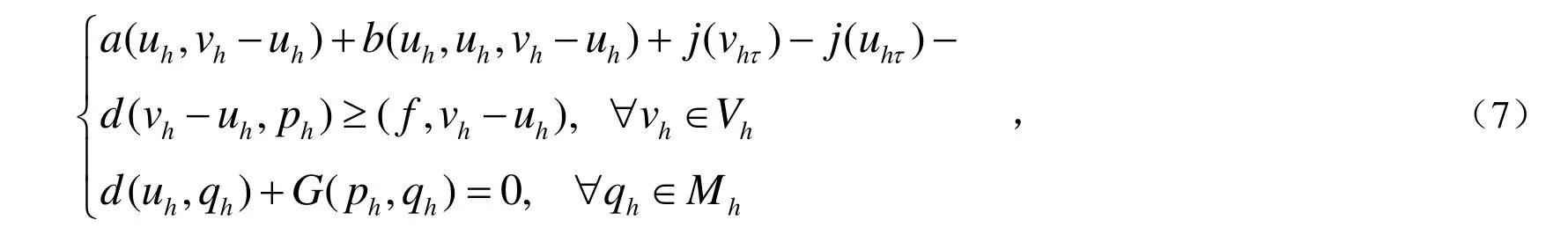
这里稳定项G（p,q）定义为：

G（p,q）=（p-Πp,q-Πq），∀p,q∈M ．

算子Π：M→P0为投影算子，且满足

定义双线性形式B：（V,M）×（V,M）→R ：B（u,p；v,q）=a（u,v）-d（v,p）+d（u,q），记

Bh（uh,ph；vh,qh）=B（uh,ph；vh,qh）+G（ph,qh）．

则离散问题（7）可以重新表示为如下形式：

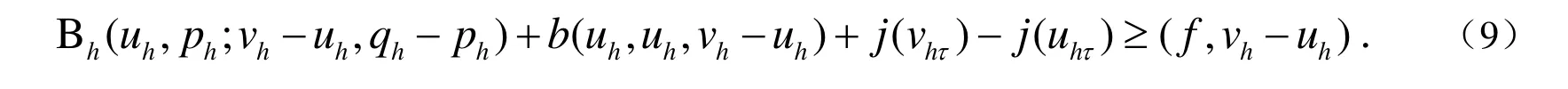
为了建立（9）式中解的存在唯一性，回顾下面在文献[2-3]中出现的稳定性定理．

定理1 对所有p∈M，假设Π为一M→P0的连续算子：

||Πp||≤c||p || ∀p∈M，则Bh满足下面的连续性：

|Bh（uh,ph；wh,rh）|≤β1（||uh||V+||ph||）（||wh||V+||rh||）,∀（uh,ph）,（wh,rh）∈Vh×Mh和弱强制性：

我们回顾在文献[6]中出现的关于离散问题（9）的解的存在唯一性和u与uh间的误差估计．

定理2 假设唯一性条件（5）成立，那么离散问题（9）存在唯一解（uh,ph）∈Vh×Mh．令（u,p）∈V×M为（4）的解，如果（u,p）足够光滑，那么有下面最优误差估计：

3 两重牛顿校正算法

令ΓH和Γh为一族直径满足0＜h＜＜H ＜1的区域Ω的正则三角形剖分．剖分ΓH和Γh的有限元空间（VH,MH）和（Vh,Mh）的定义同第二部分的定义．本文所构造的两重牛顿校正算法如下：

第一步：求（uH,pH）∈VH×MH使得对所有的（vH,qH）∈VH×MH下式成立：

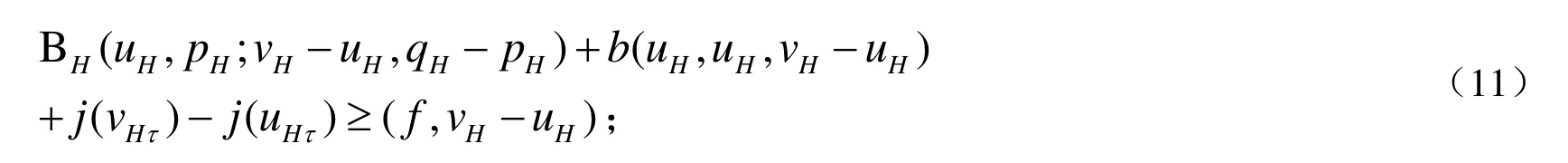
第二步：求（uh,ph）∈Vh×Mh使得对所有的（vh,qh）∈Vh×Mh下式成立：

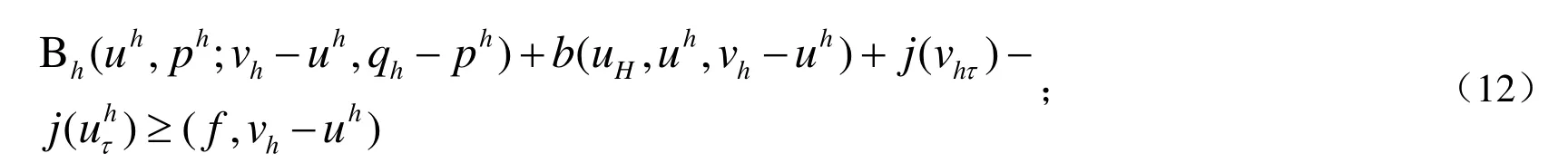
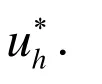
在（12）式中分别取（vh,qh）=（0,0）和（vh,qh）=（2uh,2ph），有：

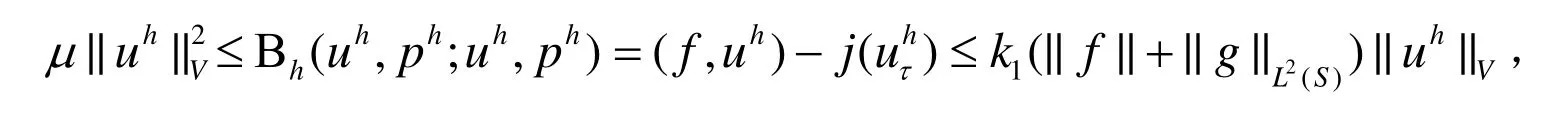
对充分光滑的（u,p），文献[4]给出了下面的误差估计：

关于问题（13），运用唯一性条件（5）和（14），有：

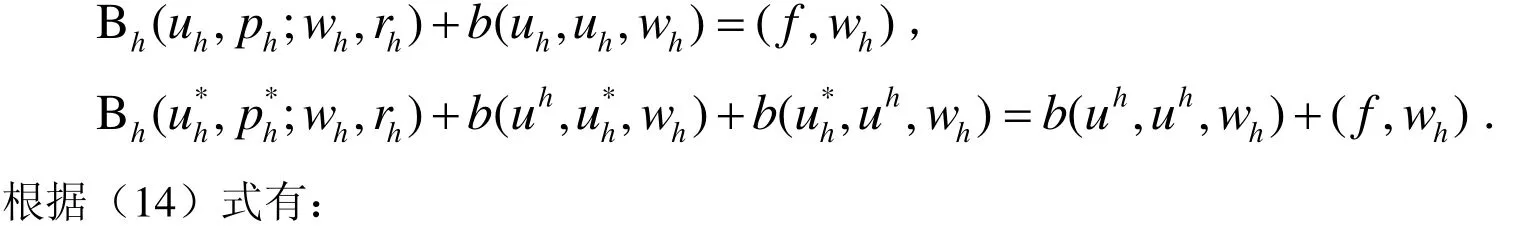
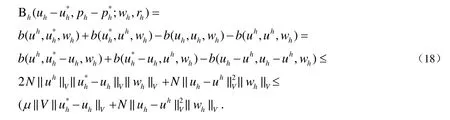
这样，从定理1有：

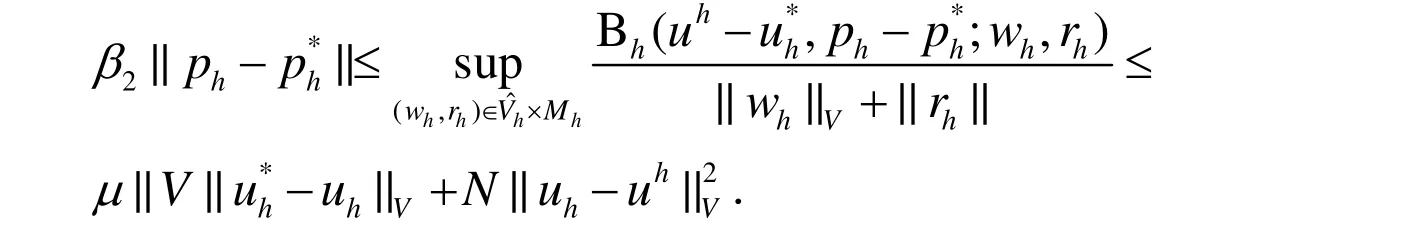
证毕．

定理3 假设（5）式唯一性条件成立，令（u,p）∈V×M和（uh*,ph*）∈Vh×Mh分别是（4）式和（13）式的解，那么对充分光滑的（u,p），有：

证明：由（10）、（15）、（16）和（17）式及三角不等式有：

[1] Fujita H. A mathematical analysis of motions of viscous incompressible fluid under leak or slip boundary conditions [J]. RIMS Kokyuroku, 1994, 888：199-216.

[2] Bochev P, Dohrmann C, Gunzburger M. Stabilization of low-order m ixed finite element [J]. SIAM J Numer Anal, 2006, 44（1）：82-101.

[3] Li J, He Y. A stabilized finite element method based on two local Gauss integrations for the Stokes equations [J]. J Comput Appl Math, 2008, 214（1）：58-65.

[4] Li Y, An R. Two-Level Pressure Projection Finite Element Methods for Navier- Stokes Equations w ith Nonlinear Slip Boundary Conditions [J]. Appl Numer Math, 2011, 61（3）：285-297.

[5] Xu J. Two-grid Discretization Techniques for Linear and Nonlinear PDEs [J]. SIAM J Numer Anal, 1996, 33（5）：1759-1777.

[6] Li Y, Li K. Pressure Projection stabilized finite element for Navier-Stokes equations w ith nonlinear slip boundary conditions [J]. Computing, 2010, 87（3-4）：113-133.

Two-level New ton Correction Algorithm for Solving Navier-Stokes Equations w ith Friction Boundary Conditions

AN Rong, WANG Xian
（School of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035）

Based on the pressure projection stable finite element method, this paper presents a two-level New ton correction algorithm for solving Navier-Stokes equations w ith friction boundary conditions. From the error estimations obtained, it can be seen that this method has the same order of convergence as one-fold stable finite element method if the fine grid scale accords w ith the formula h=O（H4）.Reference to relevant documents, it can be found that the algorithm has higher efficiency of calculation.

Navier-Stokes Equations；Friction Boundary Conditions；Stable Finite Element Method；Two-level New ton Correction Algorithm

O241

A

1674-3563（2013）01-0001-07

10.3875/j.issn.1674-3563.2013.01.001 本文的PDF文件可以从xuebao.wzu.edu.cn获得

（编辑：王一芳）

2012-06-09

国家自然科学基金项目（10901122，11001205，11126226）；浙江省自然科学基金项目（LY12A01015，Y6110240）

安荣（1980- ），男，山西太原人，副教授，博士，研究方向：偏微分方程数值解