变系数（n + 1）-维KP方程的W ronskian和Grammian解

徐 鹃

（浙江师范大学数理与信息工程学院，浙江金华 321004）

变系数（n + 1）-维KP方程的W ronskian和Grammian解

徐 鹃

（浙江师范大学数理与信息工程学院，浙江金华 321004）

基于Hirota直接方法，将变系数（n + 1）-维KP方程化成Hirota双线性形式，再借助W ronskian技巧和Pfaffian性质，对该方程进行求解，得到了其广义的W ronskian解和Grammian解．

变系数（n + 1）-维KP方程；W ronskian解；Gramm ian解

求解非线性孤子方程的精确解一直是孤立子理论中非常重要的问题．W ronskian技巧[1,2]是求非线性孤子方程解的有效方法，这种方法的主要思想是将解写成W ronskian行列式的形式，直接将N-孤子解代入方程进行验证．Gramm ian解是孤子解的另一种行列式表示[3-8]．变系数非线性发展方程在浅水波、等离子体物理等领域中有着广泛的应用，例如，变系数的KP方程比常系数的KP方程能更好地描述流体力学模型．变系数方程比常系数方程更复杂、更难求解．本文主要研究变系数的（n + 1）-维KP方程：

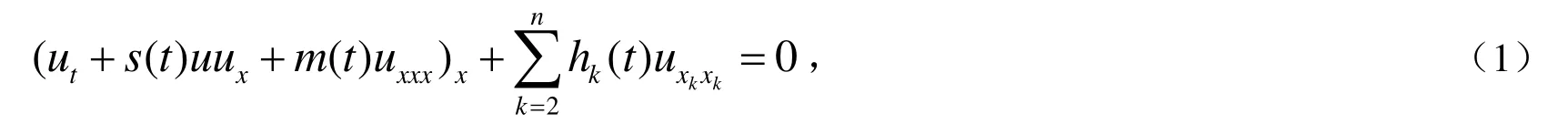
其中s（t）,m（t）和hk（t）（k≥2）xx是关于t的任意函数．方程（1）是变系数（3 + 1）-维KP方程的推广．

作变换u（x,xk,t）=12m（t）s-1（t）（ln f ），将方程（1）化为双线性形式：

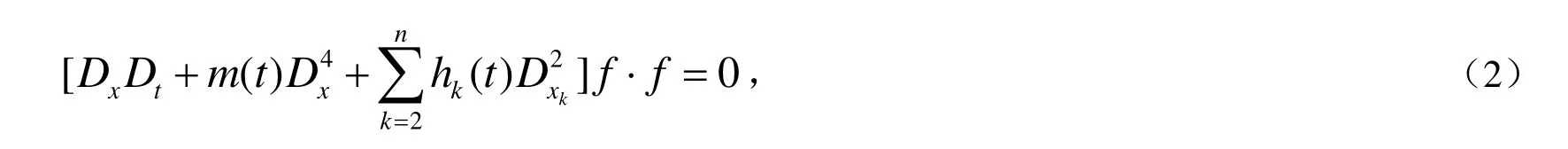
其中Hirota双线性算子Dx, Dxk,Dt定义如下：

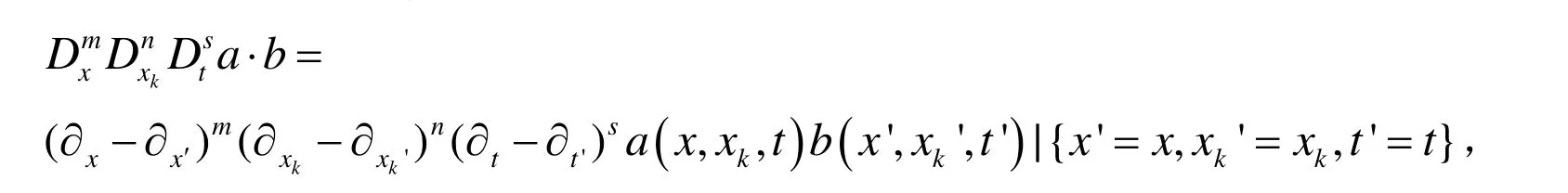
显然（2）可以写成非线性偏微分方程进而得到：

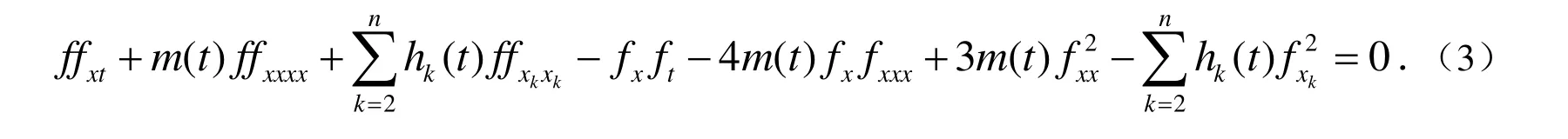
下面利用W ronskian技巧和Pfaffian性质来求解变系数（n + 1）-维KP方程的W ronskian和Grammian解．

1 变系数（n + 1）-维KP方程的Wronskian解

结论1 双线性方程（2）的N孤子解有如下W ronskian行列式表示：

证明：根据W ronskian行列式的性质以及函数φ满足的条件（5），容易得到f对变量的各阶导数为：

将以上这些导数带入方程（3）的左边，经过简单计算可以得到：

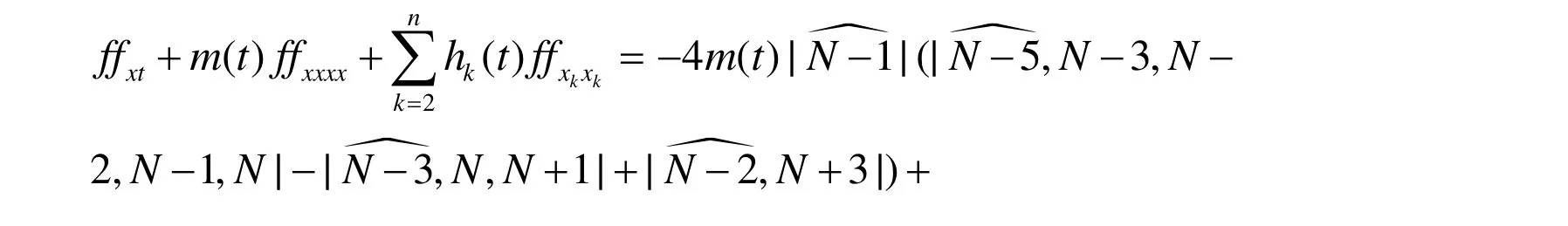
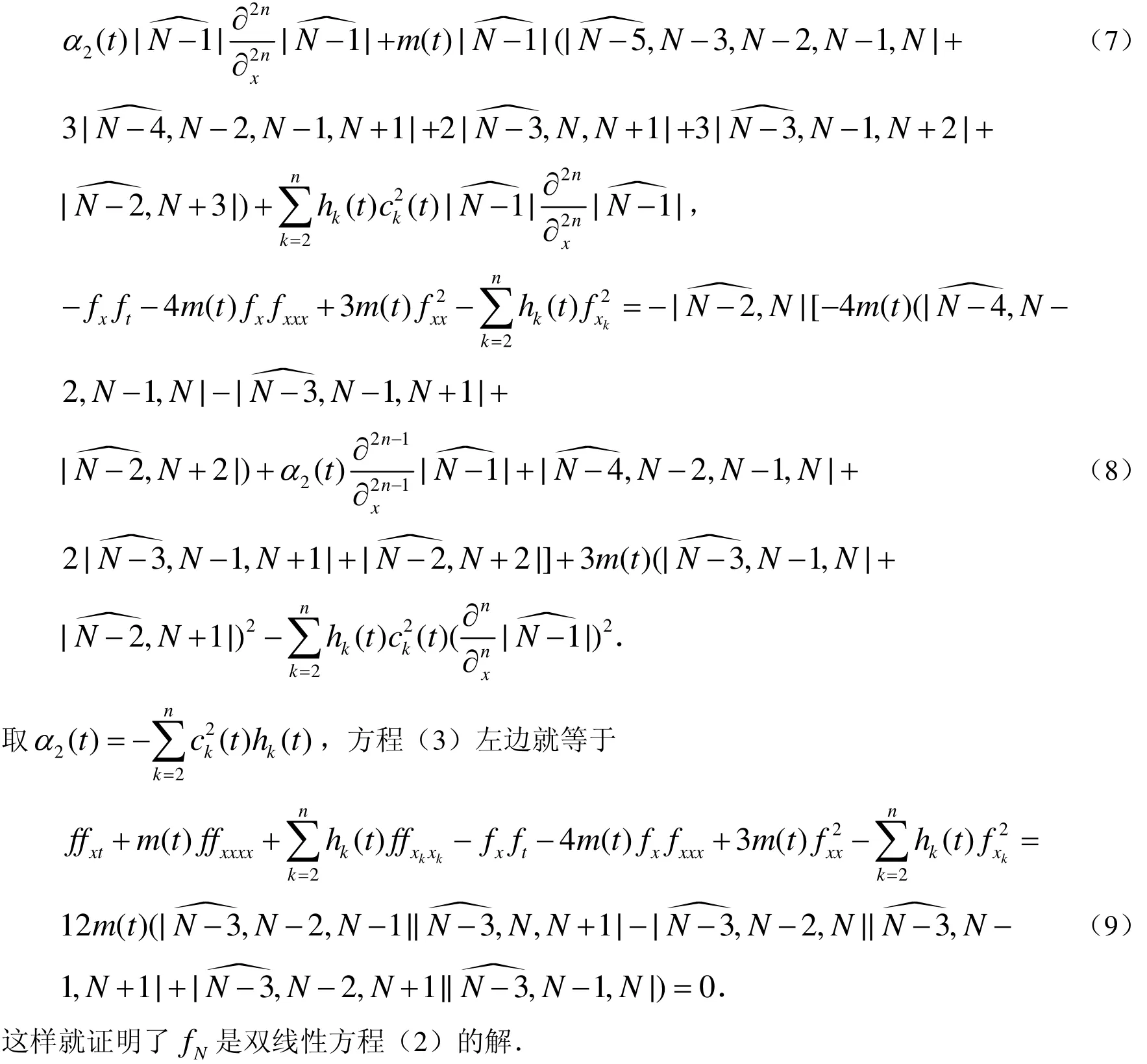
2 变系数（n + 1）-维KP方程的Gramm ian解

接下来介绍Pfaffian元素，定义如下：

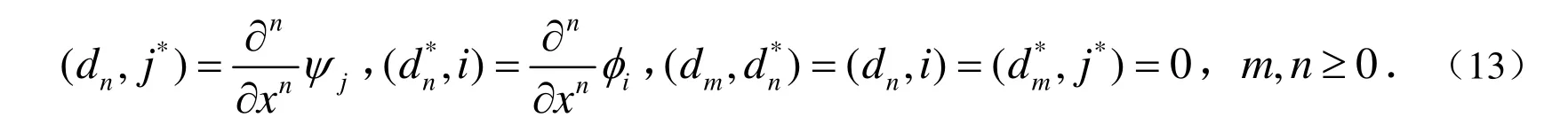
根据上述定义，Pfaffian元素aij对变量x,xk,t的导数分别为：

如果记fN=（1,2,…,N,N*,…,2*,1*）=（·），那么可以得到fN对变量的各阶导数为：

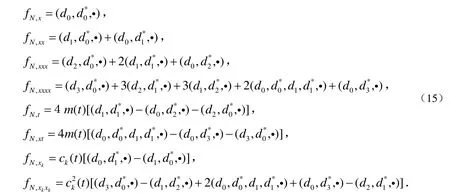
根据Pfaff的性质和运算法则，很容易得到下面恒等式：

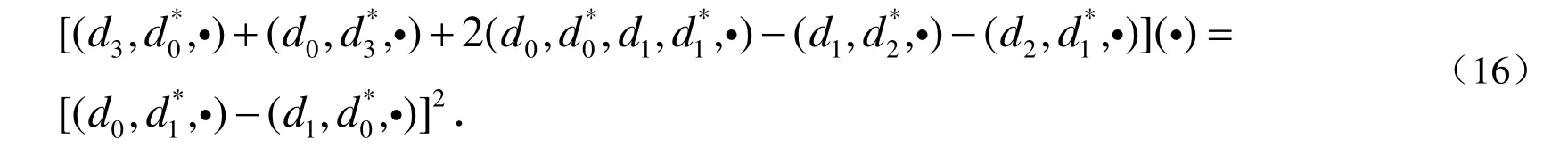
将（15）式和恒等式（16）式代入双线性方程的展开式（3），经过计算可以得到：

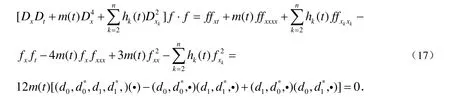
很明显，（17）式是一个Jacobi恒等式，它的值为0．于是Gramm ian行列式fN是双线性方程（2）的一个解．

3 结束语

在本文中，构造了变系数（n + 1）-维KP方程的W ronskian和Grammian解，结果表明，方程（1）有丰富的Wronskian行列式解．当然方程（1）还存在其它的更广义的Grammian解，这也是笔者要继续研究的内容．

[1] Freeman N C, Nimmo J J C. Soliton solutions of the Korteweg-de Vries and Kadom tsev-Petviashvili equations：The Wronskian technique [J]. Phys Lett A, 1983, （95）：1-3.

[2] Nimmo J J C, Freeman N C. The use of Bäcklund transformations in obtaining N-soliton solutions in Wronskian form [J]. J Phys A：Math Gen, 1983, （17）：1415-1424.

[3] Ma W X. Wronskian and Grammian solutions to a （3+1）-dimensional generalized KP equation [J]. Appl Math Comput, 2011, （217）：10016-10023.

[4] Yu G F, Hu X B. Extended Gram-type determinant solutions to the Kadom tsev-Petviashvili equation [J]. Math Comput Simul, 2009, （80）：184-191.

[5] Wu J P, Geng X G. Gramm ian determ inant solution and Pfaffianization for a （3+1）-dimensional soliton equation [J]. Commun Theor Phys, 2009, （52）：791-794.

[6] Zhang Y, Cheng T F, Ding D J, et al. Wronskian and Gramm ian solutions for （2+1）-dimensional soliton equation [J]. Commun Theor Phys, 2011, （55）：20-24.

[7] Zhang Y, Lv Y N. On the nonisospectral modified Kadom tsev-Peviashvili equation [J]. J Math Anal Appl, 2008, （342）：534-541.

[8] Ye L Y, Lv Y N, Zhang Y. Gramm ian solutions to a variable-coefficient KP equation [J]. Chin Phys Lett, 2008, （25）：357-358.

Wronskian and Gramm ian Solutions to the （n + 1）-dimensional KP Equation w ith Variable Coefficients

XU Juan
（College of Mathematics, Physics and Information Engineering, Zhejiang Normal University, Jinhua, China 321004）

The paper explored the process of the generalized W ronskian and Gramm ian solutions. The steps mainly include：to change the variable-coefficient （n + 1）-dimensional KP equation to bilinear form based on Hirota method, and then to solve the equation w ith the help of Wronskin technique and Pfaffian properties.

Variable-coefficient （n + 1）-dimensional KP Equation；Wronskian Solution；Grammian Solution

O175.12

A

1674-3563（2013）01-0013-05

10.3875/j.issn.1674-3563.2013.01.003 本文的PDF文件可以从xuebao.wzu.edu.cn获得

（编辑：王一芳）

2012-06-08

徐鹃（1989- ），女，浙江衢州人，硕士研究生，研究方向：系统理论