复杂边界非饱和模型有限元数值模拟

王 芳，杨虎山

（忻州师范学院数学系，山西忻州 034000）

复杂边界非饱和模型有限元数值模拟

王 芳，杨虎山

（忻州师范学院数学系，山西忻州 034000）

利用有限元集中质量法对一维复杂边界土壤水分运动数学模型（非饱和Richards模型）进行了数值模拟，并进行了模型验证．模型验证结果表明，该方法计算精度很高，符合实际工作要求．

土壤水分运动；有限元；数值模拟

非饱和土壤水分运动模型可用一类非线性的对流扩散方程表示．研究此类问题，对干旱半干旱地区的土壤水分预测尤为重要，对发展节水型农业有重要意义．

非饱和土壤水分运动问题可归结为下面的模型方程：

求h（z ,t ）使得对于任意的T＞0，满足：

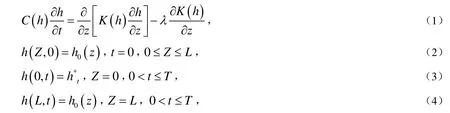
其中，λ为指标变量；h（L）为负压水头（cm）；C（h）为比水容量（1cm）；K（h）为非饱和导水率（cmm in）；Z为空间坐标（cm）；h0（z ）为土壤的初始负压水头（cm）；为变量，是随时间t变化的水头值（cm），在实际计算时，采用插值函数进行处理；L和T分别是空间和时间变化的上界．

对有关渗透问题的一维非饱和流问题的研究[1-3]，用有限差分法[4]对方程进行离散时，结果对边界条件以及土壤参数极为敏感．本文通过变分的办法将其直接转化为已知通量的计算，较好地解决了这类边界条件问题．

1 数学模型的建立

1.1 基本假定

1）各层土壤均质且各向同性；

2）入渗水流为连续介质且不可压缩，在土壤水分运动过程中，土壤骨架不变形．

1.2 方程的离散

方程（1）中，由于比水容量C（h）和非饱和导水率K（h）为基质势h的函数，所以方程（1）属于二阶非线性偏微分方程，除少量问题外，一般情况下求解析解是困难的，须使用数值求解．下面考虑方程（1）在初始条件（2）及上、下边界条件（3）、（4）的定解问题，以此说明本模型的数值模拟过程．

这里的（·,·）表示区域Ω上的L2内积，以下类同．

1.2.1 半离散有限元逼近

先在空间方向上用有限元逼近[6]，对Ω=（0,L）进行有限元剖分：

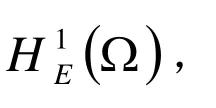
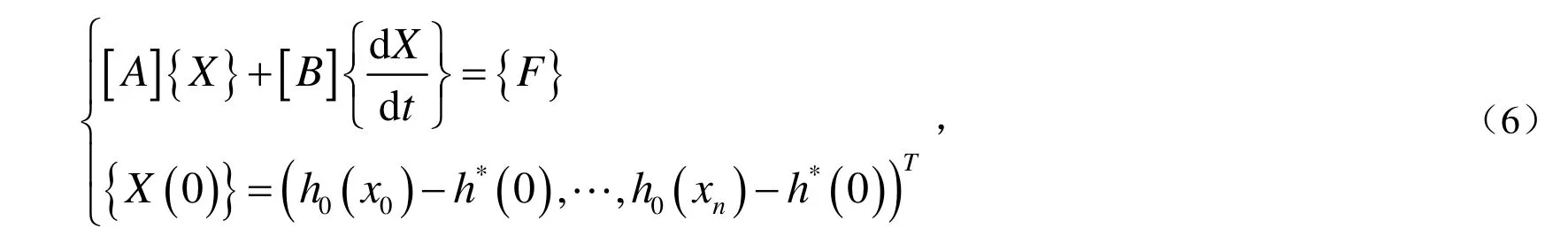
其中，

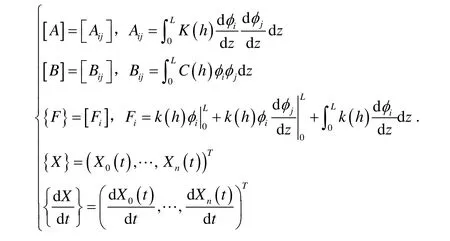
方程（6）定义了一类非线性常微分方程组，要数值求解，仍须对时间变量离散化．

1.2.2 全离散格式

在时间方向上引入有限差分格式逼近矩阵方程的时间导数．

对时间t进行离散，设时间步长为Δt，tm=mΔt ．在时间层m与m+1之间，tm≤t≤tm+1，将变量t变换到变量τ，t=（m +τ）Δt，其中0≤τ≤1．

在tm≤t≤tm+1，对Xj（t）进行线性插值，令

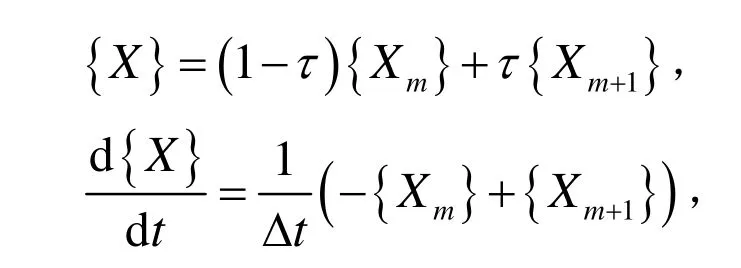
其中，{Xm}=（X1（mΔt）,X2（mΔt）,…,Xn（mΔt ））T，{Xm+1}也类似．

同理也可对{F}进行插值．这样方程（6）可化为：

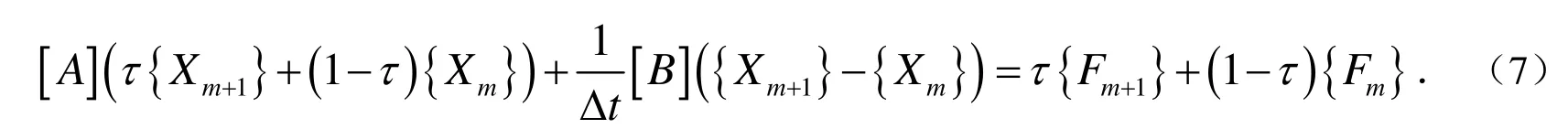
若（7）两边乘上一个非负的权函数，记为w，再令τ从0到1积分，就得到：

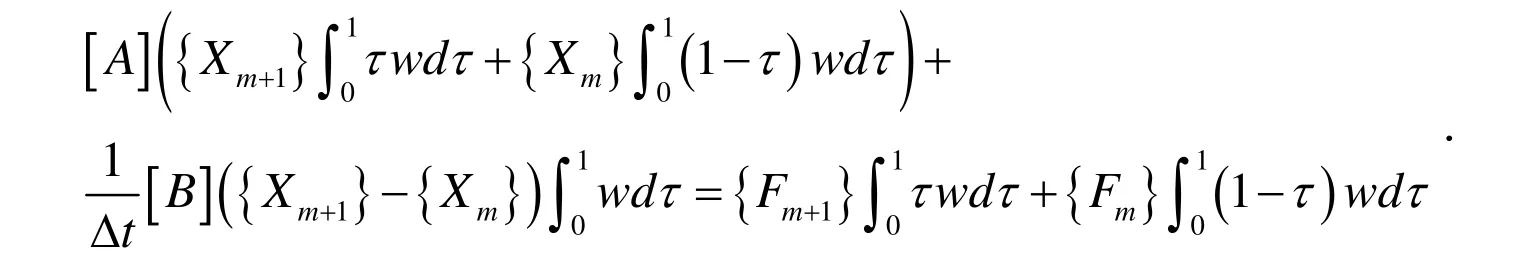
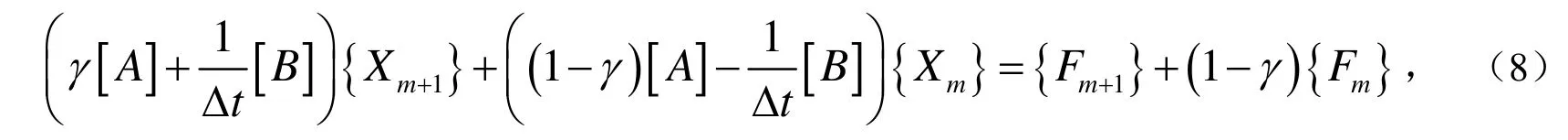
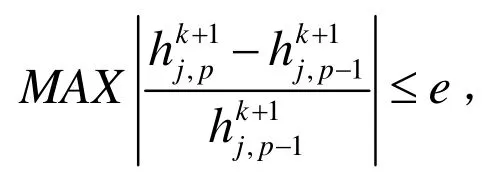
2 数值模拟

用本文所建立的有限元集中质量法的数值模型对山西省太谷县三台村的扰动黄土土样[7]进行数值模拟．解决非饱和土壤水分运动数值模拟的求解问题，土壤非饱和导水率、水分扩散率、土壤水分特征曲线3个土壤水分运动参数是必不可少的重要数据．其中，土壤水分特征曲线是定量描述和预测土壤水分运动的重要基础．一般地，水分特征曲线的经验模型可分为幂函数、指数函数、双曲线余弦函数和误差函数4类[8]，其中，幂函数模型是描述土壤水分特征的最普遍模型[8]．本文采用较常用的指数形式：

式中，s为土壤水吸力（cm）．非饱和导水率的测定有直接法和间接法两种[4]．由于直接测定法耗时多、昂贵、繁琐，且测定范围较窄，可获得的实验数据不能代表土壤水分特征的完整关系，因此许，多研究提出了间接推求导水率的方法[4]．本文采用较常用的指数形式，推求得土壤非饱和导水率K与负压水头h的关系为：

利用土壤水分特征曲线，推求得土壤比水容量C与负压水头h的关系为：

C（h）=3.42×10-6e9.3865（8.045-ln（-h））-9.3865

土壤水分运动的初始和边界条件为：

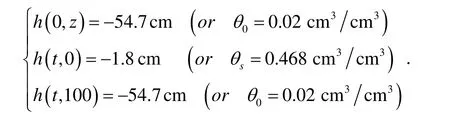
将区域Ω=（0,100），每个单元的长度为1cm，时间步长Δt=5s，模拟1小时，将这些数据输入该程序，得到入渗率分布图，如图1所示．

图1 垂直入渗率与时间的关系曲线

从图1可知，本文所得到数值模拟结果与文献[7]提到的试验结果是相吻合的．从图中还可以看出入渗率的变化规律：从入渗开始到0.1h这一段时间，入渗率从0.2迅速下降到0.04以下，此后，地表层z = 0处的入渗率变化不大，然后地表逐步接近饱和含水率．

3 结语

本文利用非饱和流方程，建立了变水头非恒定水位复杂边界条件下一维变水头均质水入渗及土壤水分运动的数学模型．对于入渗边界条件，通过变分的办法将其直接转化为已知通量的计算，从而较好地处理了边界条件问题．在每一个新的时间层，利用插值函数近似代替通过试验实测的负压水头．数值模拟结果表明，采用非饱和流方程可以很好地模拟均质土壤一维变水头的土壤水分运动，该方法对田间土壤水分的预测预报有重要意义．

[1] Haverkamp R, Vauclin M, Touma J, et al. A comparsion of numerical simulation models for one-dimensional infiltration [J]. Soil Science Society of America Journal, 1977, 41：285-294.

[2] Ciarlet P C. The finite element methods for elliptic problems [M]. Amsterdam：NorthHolland, 1978：1-50.

[3] Vachaud G, Thony J L. Hyteresis during infiltration and redistribution in a soil column at different initial water contents [J]. Water Resources Research, 1971, 7：111-127.

[4] 雷志栋, 杨诗秀, 谢森传. 土壤水动力学[M]. 北京：清华大学出版社, 1988：270-319.

[5] Adams R A. Sobolev spaces [M]. New York：Academ ic Press, 1975：26-27.

[6] O. C. Zienkiew icz. 有限元法[M]. 尹泽勇, 柴家振, 译. 科学出版社, 1985：445-473.

[7] 王芳, 孙西欢, 马娟娟, 等. 不同水头作用下土壤垂直入渗特性试验研究[J]. 山西水利, 2005（1）：75-76.

[8] Van Genuchten M Th, Leij F J. Indirect Methods for Estimating the Hydraulic Properties of Unsaturated Soils [M]. California：University of California Press, 1992：1-14

A Finite Element Numerical Simulation for Unsaturated Richards Model w ith Complex Boundary

WANG Fang, YANG Hushan
（Department of Mathematics, Xinzhou Teacher’s College, Xinzhou, China 034000）

Through the method of the lumped mass of the finite element, the paper implements the numerical simulation and the model validation toward the mathematical model of the complex one-dimensional boundary soil water movement （unsaturated Richards model）, the results of the model validation show that this method possesses a very high accuracy of calculation which is in line w ith the requirements of the practical work.

Soil Water Movement；Finite Element；Numerical Simulation

O241.82

A

1674-3563（2013）01-0031-05

10.3875/j.issn.1674-3563.2013.01.006 本文的PDF文件可以从xuebao.wzu.edu.cn获得

（编辑：王一芳）

2012-03-06

王芳（1978- ），女，河南焦作人，讲师，硕士，研究方向：偏微分方程数值模拟，运筹学