考虑折点半径的折线先张梁钢铰线力学性能试验研究

黄文雄，谭利英

（1.长江大学 城市建设学院，湖北 荆州434023；2.长江大学 设计研究院，湖北 荆州434023；3.荆州市城市规划设计研究院，湖北 荆州434000）

折线配筋预应力混凝土先张梁采用了与受力相适应的布筋方式，解决了先张梁跨度较小的不足，是一种同时具备先张法与后张法结构优点的新型结构；弯起器是其得以实现的关键构件［1－2］。目前工程中弯起器主要有滚轴式与拉板式2种，由于受结构尺寸与构造要求限制，难以对起弯点进行过多考虑，易使预应力筋在起弯点处形成“折点”，导致钢绞线极限强度折减、延性性能降低以及预应力摩阻损失增大，在影响结构力学性能的同时，更严重降低了结构在施工与使用中的安全性［3－6］。

选取特定半径R与弯折角度θ，设计相应试验方案，研究了不同导向半径R与弯折角度θ条件下弯起器对钢绞线力学性能的影响规律，并深入分析了试验现象与影响规律的产生机理［7－9］；同时以试验数据为基础，基于摩阻系数μ变化规律的具体特点，提出了考虑不同导向半径R影响的钢绞线弯折摩阻预应力损失统一计算公式，为折线配筋先张法预应力混凝土先张梁的深入研究与推广应用提供了设计依据与试验数据支持。

1 试验方案

试验采用卧位试验的安装加载方案，分为直拉试验与弯折拉试验：直拉试验用于钢绞线基本参数的测定，并作为弯折拉试验的基础对比试验；弯折拉试验用于钢绞线弯折极限强度、延性，以及钢绞线弯折预应力摩阻损失的测定［10］。选用R＝10、19.5、50、100、600mm共5组半径作为试验用导向构件半径；考虑工程实际的多样与复杂，选取θ＝4.35°、6.45°、8.65°、10.75°、12.85°、14.95°作为试验折角，设计了10组如图1所示的盒状弯起器。

图1 钢绞线弯折拉试验方案示意图

图2 盒式弯起器的就位与钢绞线的布置情况（Box10，R＝600mm）

选取位于盒状弯起器两端外侧的Ⅰ、Ⅳ截面与位于盒状弯起器3块导向构件中间的Ⅱ、Ⅲ截面作为应变测试截面；选取F＝20kN作为初始荷载，20%Fm、30%Fm、40%Fm、50%Fm、60%Fm、70%Fm、75%Fm、80%Fm作为特征荷载，如图2所示。试验时在初始荷载F＝20kN处开始由QXL－5000试验系统记录F Δl拉伸试验曲线，同时记录其极限拉力与相应伸长量，以分析钢绞线弯折极限强度与延性变化情况；在初始荷载与特征荷载时持荷1min后采用DH－3816多测点静态应变测试系统记录各应变测点的应变值，以分析钢绞线弯折预应力摩阻损失情况。

2 试验结果

根据试验目的与试验方案，共进行了42组钢铰线的拉伸试验：直拉试验3组；5种导向半径6种弯折角度每组一根钢绞线共30组；另选取R＝10、19.5、600mm 3种导向半径的常用折角θ＝4.35°、6.45°与最大折角θ＝14.95°的9组作为校核试验。

2.1 钢绞线极限强度与弯折延性

以钢绞线强度折减系数η来表征钢绞线极限强度变化规律；以屈服伸长率Ayt来表示钢绞线延性性能，其中钢绞线的屈服荷载取Fy＝85%·Fm＝220kN［11］。钢绞线弯折拉强度折减系数η、屈服伸长率Ayt随导向半径R、弯折角度θ的变化情况绘于图3～图4。部分钢绞线破坏状态如图5所示。

1）破坏特征：直拉试验与R较大（R＝600mm）的弯折拉试验时，钢绞线一般在试件锚固端部（1根或多根）或应变片粘贴处（1根）破断。而R较小（R≤50mm）的弯折拉试验时钢绞线多在中间折点破断；且θ较小时多为多根破断，θ较大时多为与中间折点紧密接触的1根钢丝破断，同时破断点处钢筋压痕明显，并形成明显“折点”；但R＝100mm时其破坏特征比较复杂。

2）极限抗拉强度与R及θ的关系：随着θ的增大，钢绞线弯折强度折减系数ηs呈抛物线趋势增大，R越小抛物线曲率越大；随着R的增大，ηs在半对数坐标系中呈下降趋势，且θ较小时呈现线性下降，θ较大时呈抛物线下降；而当R≥100mm时，ηs随θ与R的变化曲线均趋于平缓。说明R较小时θ与R变化对钢绞线极限抗拉强度将产生显著影响，且影响程度随R的减小、θ的增大而加剧；而R较大时θ与R变化对钢绞线极限抗拉强度影响则较小。故而弯起器的导向半径R在构造要求容许时应尽量取大值，受限时R也宜不小于100mm。

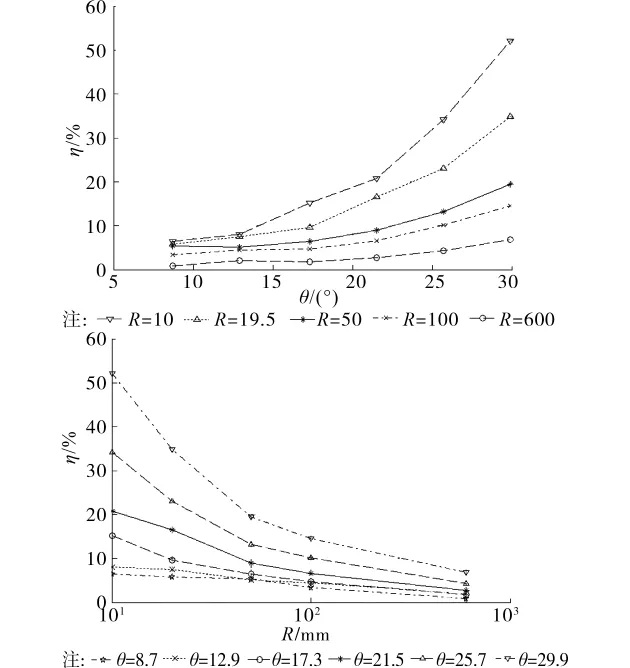
图3 钢绞线弯折拉强度折减系数η随弯折角度θ、导向半径R的变化曲线

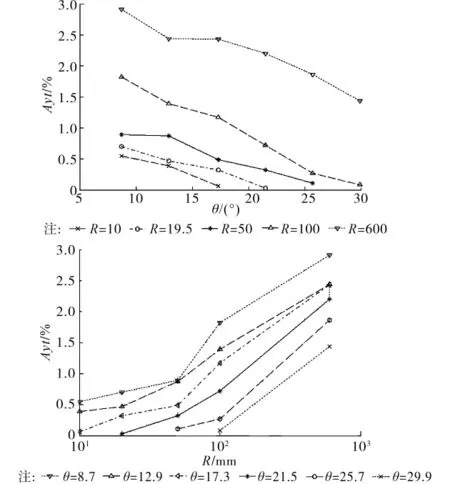
图4 屈服伸长率Ayt随弯折角度θ、导向半径R的变化曲线

图5 部分拉伸试验钢绞线破坏状态（左侧：R019A6－1，中间折点断1根，折角与压痕明显；右侧：R600A6－1，应变片粘贴处断1根）

3）延性性能与R及θ的关系：随着θ的增大，Ayt基本上呈线性下降；随着R的增大，Ayt在半对数坐标系中呈现出抛物线上升的趋势，其规律与fpu基本相似；说明较小的R与较大的θ同样会大大降低钢绞线的延性性能。同时，当R＝600mm，θ＝8.7°→29.9°时，fpu折减了6.05%，而Ayt折减了47.12%；θ＝8.7°，R＝600mm→10mm 时，fpu折减了5.63%，而Ayt折减了75.64%；说明θ的增大与R的减小对钢绞线延性性能的折减远远大于对极限强度的影响；特别是当R＝100mm时，在常用折角范围内强度折减已基本在5%以内，但其延性的折减却仍在50%左右。从延性性能来看，弯起器导向半径R应取得更大一些。

2.2 弯折摩阻预应力损失

由于弯折角θ一般较小，由文献［12－16］弯起器弯折摩擦阻力损失计算可简化为如图6所示［12－16］。钢绞线弯起角度为θ，弯起端轴向应力为σ1，其竖向向上分力σ1sinθ由弯起器承受，钢绞线同时也受到弯起器的反作用力σ1sinθ；水平端轴向应力为σ2。此时，弯起器弯折摩擦阻力损失σl1可表示为：

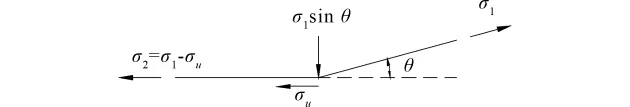
图6 弯起器弯折摩擦阻力损失计算简图

故而摩擦系数μ：

试验后由Ⅰ、Ⅳ截面与Ⅱ、Ⅲ截面各测点应变（或其增量）的平均值）可计算对应导向半径R对应弯折角度θ的弯起器摩擦系数μ。

1）测试数据的分析与处理：直拉试验时各测点测试应变值随拉力的增大基本呈线性增加，在相同拉力作用下各应变片测试结果基本一致。弯折拉试验时，虽测试应变随拉力也呈增加趋势，但测试数据有一定起伏，同一截面或相同测试条件不同测点之间测试数据相差也较大。深入分析可知：测试数据虽有起伏，但起伏趋势将随着拉力的增大逐渐变缓；相同测试条件不同测点之间测试数据相差虽然较大，但拉力较大时其应变增量相差较小。故而可以采用拉力较大时钢绞线各测点应变增量形式来计算对应试验条件的弯起器摩阻系数μ；综合分析所有测试数据后，选用特征荷载50%～60%～70%～80%Fm时测点应变增量来进行摩阻系数μ的分析，分析结果绘于图7所示。

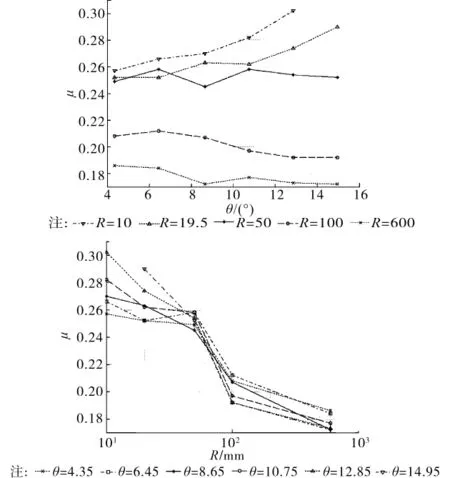
图7 摩阻系数μ随弯折角度θ、导向半径R的变化曲线

2）摩阻系数μ与R及θ的关系：随R的增大，在半对数座标系中摩阻系数μ呈“S”形曲线下降；θ的变化虽对μ会产生一定影响，但影响程度远小于R。当R≤50mm时，摩阻系数μ随着R的增大而减小，随着θ的增大而增大；当R≥100mm时，摩阻系数μ随着R与θ的增大逐渐减小，但趋势平缓；当50mm＜R＜100mm时，摩阻系数μ随着R的增大急剧减小，而且θ越大μ的减小趋势越剧烈，曲线在此区间呈现交叉现象；相比而言，R变化对摩阻系数μ的影响程度远大于θ变化所产生的影响。

2.3 机理分析

1）破坏特征与应变数据起伏：锚固因素将会使钢绞线端部受力复杂，而应变片粘贴时钢丝的打磨将会对钢绞线造成一定损伤，所以在直拉或R较大的弯折拉时钢绞线一般会在端部锚固区或应变片粘贴处断裂。而当R较小时，钢绞线将在起弯点形成弯折，从而产生相应塑性变形与应力集中现象，严重影响钢铰线的强度、塑性与韧性，形成一种“折点”效应；“折点”效应随着R的减小、θ的增大而加剧，形成了相应的破坏特征。同时，“折点”处钢绞线弯折时各根钢丝弯折曲率半径不同而变形不一致，将产生较大附加内力与变形，导致相同测试条件不同测点间应变测试数据相差较大；但随着拉力的增大，折点所附加的内力与变形将会逐渐趋于稳定；故而拉力较大时实测应变增量基本一致。

2）强度与延性：折点处应力集中现象随着R的减小、θ的增大而加剧，所以钢绞线的强度与延性会随着R的减小、θ的增大而逐渐变小。当R较小时，“折点”效应随θ增大显著加强，导致强度与延性的折减呈抛物线趋势增大；而随着R的增大，钢绞线与导向构件间相互作用面增大，折点处应力集中现象将会迅速减小，所以钢绞线强度与延性随R的增大呈现对数曲线下降的趋势。但由于钢绞线只有进入塑性后才能表现出延性，各种影响因素一旦对钢绞线强度产生折减，则将大大降低钢绞线塑性，从而严重影响其延性性能；所以，θ的增大与R的减小对钢绞线延性性能的折减远远大于其对极限强度的影响。

3）摩阻系数μ：R较小时“折点”效应起主导作用，R较大时作用面积占据主导地位；故而R较小时，μ随θ的增大而增大；R较大时，μ随θ的增大而减小；而50mm＜R＜100mm时，由于接触作用面积的增大导致折点处应力集中现象急剧减小，而使接触面积逐渐占据主导地位，所以μ随着R的增大急剧减小。

3 钢绞线弯折摩阻预应力损失的计算

由上分析可知：虽然θ的变化会对摩阻系数μ会产生一定影响，但影响程度远小于R；故而，在建立弯起器弯折摩阻预应力损失计算公式时可以在考虑一定保证率后忽略θ对摩阻系数μ的影响，但不能忽略R对摩阻系数μ所产生的影响。

同时，基于摩阻系数μ随R变化所呈现出的“S”形曲线的影响规律可知：R的变化将摩阻系数μ分成明显的三段。故而在建立钢绞线弯折摩阻预应力损失的计算公式时可以考虑采用统一的计算公式，但弯折摩阻系数μ根据实际导向半径R的大小来分段选取。

由弯起器弯折摩擦阻力损失计算简图（如图6），弯起器弯折摩擦阻力损失σl1可初步表达为：

基于摩阻系数μ随R的变化规律，通过对所有实测试验数据的分析，对于弯起器弯折摩阻系数μ的取值可分3种情况来考虑：

1）当R≤50mm时，对摩阻系数μ的59个实测试验样本统计分析可知其符合μn＝0.261、σn＝0.018 6的正态分布，试验样本变异系数CV ＝0.071，考虑结果离散与工程安全，取95%的保证率时μ＝0.29。

2）当R≥100mm时，对摩阻系数μ的45个实测试验样本统计分析可知其符合μn＝0.188、σn＝0.0169的正态分布，试验样本的变异系数CV＝0.090，取95%的保证率时μ＝0.22。

3）当50mm＜R＜100mm时：μ＝0.29～0.22，按线性内差。

参考相关资料，为了增加θ较大时弯起器弯折摩擦阻力损失σl1计算公式逻辑上的合理性，也为了公式形式的统一性，弯起器弯折摩擦阻力损失σl1可进一步表达为：

式中：σl1为弯起器弯折摩擦阻力损失；σcon为预应力钢筋锚下张拉控制应力，MPa；θ为钢绞线弯起角度。

μ为弯起器的摩擦系数，根据实际导向半径R大小来选取；R≤50mm时μ＝0.29，R≥100mm时μ＝0.22，50mm＜R＜100mm时μ＝0.29～0.22，按线性内差。

以50%Fm为基准荷载，将弯起器摩阻损失计算结果与试验实测数据点绘于图8。可以看出实测数据与计算值符合较好，且大部分试验数据点接近或位于公式（3）计算结果的下方，计算公式有一定的保证率。

图8 弯起器摩阻损失计算结果与试验实测数据比较

4 结 论

1）钢绞线极限抗拉强度折减率ηs随θ的增大呈抛物线趋势增大，随R的增大呈对数曲线趋势减小；当R≥100mm时，R与θ的变化对钢绞线极限抗拉强度fpu的影响较小；说明弯起器的导向半径R在构造要求容许时应尽量取大值，受限时R也不宜小于100mm。

2）钢绞线的延性随θ与R的变化规律其规律与fpu基本相似，但θ与R的变化对钢绞线延性性能的折减效应较对fpu更加显著；从延性性能来看，在满足结构尺寸与构造要求的情况下，弯起器的导向半径R应该取得更大一些。

3）当R≤50mm或R≥100mm时，弯起器弯折摩阻系数μ随R与θ呈增大或减小趋势，但变化趋势并不显著；而当50mm＜R＜100mm时，摩阻系数μ随着R的增大急剧减小，θ越大变化越剧烈。

4）基于摩阻系数μ随R与θ的变化规律，弯起器弯折摩阻预应力损失可由公式σl1＝σcon［1－e－（μθ）］计算，式中摩擦系数μ 根据实际导向半径R大小来选取；R≤50mm时μ＝0.29，R≥100mm时μ＝0.22，50mm＜R＜100mm时μ＝0.29～0.22，按线性内差。

［1］黄文雄.基于新型弯起器的折线配筋先张梁力学性能研究［D］.武汉：华中科技大学，2012.

［2］Amom W，Tuan C Y，Tadros M K.Curved，precast，pretensioned concrete I－girder bridges ［J］.PCI Journal.2008，53（6）：48－66.

［3］黄文雄，谭利英.结构与材料参数变化对折线配筋先张梁局部应力的影响［J］.公路交通科技，2012，29（1）：75－79.Huang W X，Tan L Y.Impact of structural parameters and material parameters on local stress distribution in polyline pretensioned beam ［J］.Journal of Highway and Transportation Research and Development，2012，29（1）：75－79.

［4］黄文雄，谭利英.折线配筋先张梁中弯起器的模拟及其对局部应力的影响分析［J］.中外公路，2012，32（5）：132－135.Huang W X，Tan L Y.Study on the bend component simulation method and its effects on the local stress distribution in the polyline pretensioned beams［J］.Journal of China ＆ Foreign Highway，2012，32（5）：132－135.

［5］黄文雄，谭利英.折线配筋先张梁折点半径优化［J］.公路，2012（10）：54－56.Huang W X，Tan L Y.Simulation of the prestressed reinforcement and key points in modeling ［J］.Highway，2012（10）：54－56.

［6］陈汉昌，刘立新，宋明慧，等.折线先张梁中钢绞线力学性能的试验研究［J］.建筑技术，2010，41（12）：1108－1111.Chen H C，Liu L X，Song M H，et al.Test research on mechanical property of steel strand in fold－line pretension concrete beam ［J］.Architecture Technology，2010，41（12）：1108－1111.

［7］Huang W X，Tan L Y，Yang H Y，et al.Discussion on curve prestressed reinforcement simulation in FEA ［J］.Applied Mechanics and Materials，2012（178－181）：2179－2182.

［8］Huang W X，Tan L Y.New Exploration on prestressed reinforcement simulation in FEA of prestressed concrete［C］／／2012International Conference on Electric Technology and Civil Engineering （ICETCE 2012），Three Gorges，Hubei，China：IEEE eXpress Conference Publishing，2012.

［9］Huang W X，Tan L Y.Analysis of local stress and improvement of stress state on key parts of the polyline pretensioned beam ［C］／／2012International Conference on Electric Technology and Civil Engineering（ICETCE 2012），Three Gorges，Hubei，China：IEEE eXpress Conference Publishing，2012.

［10］Sankar G S，Shetty V S，Karanth H S D.A comparative study of physical and mechanical properties of the different grades of Australian stainless steel wires［J］.Trends in Biomaterials and Artificial Organs，2011，25（2）：67－74.

［11］Budzik R，Glis B，Wludzik R，et al.Estimation of standard PN－EN 10264steel wire for rope［J］.Wire Journal International，2010，43（1）：64－69.

［12］中华人民共和国交通部.公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京，2004.

［13］刘立新，胡丹丹，于秋波，等.先张法折线形预应力梁钢绞线摩擦损失试验研究［J］.郑州大学学报：工学版，2006，27（4）：6－9.Liu L X，Hu D D，Yu Q B，et al.Experimental studies on pre－stressing frictional loss of the fold－line pretension pre－stressed beam ［J］.Journal of Zhengzhou University：Engineering Science，2006，27（4）：6－9.

［14］Cheng H，Yang P，Cheng Q.Frictional resistance analysis on prestressed curved channel under cosine distribution assumption of contact pressure ［C］／／Piscataway，NJ，USA：IEEE，2011.

［15］Robitaille S，Bartlett F M，Youssef M A，et al.Evaluating prestress losses during pre－tensioning［C］／／St.Johns，NL，Canada：Canadian Society for Civil Engineering，2009.

［16］Zhou Z，He J，Chen G，et al.A smart steel strand for the evaluation of prestress loss distribution in posttensioned concrete structures［J］.Journal of Intelligent Material Systems and Structures，2009，20（16）：1901－1912.