全时域初值推进边界元法分析氯盐侵蚀下混凝土结构服役寿命

蒋琼明，杨绿峰，2，陈 正

（1.广西大学 土木建筑工程学院；工程防灾与结构安全教育部重点实验室，南宁530004；2.广西壮族自治区 住房和城乡建设厅，南宁530028）

暴露在氯盐环境下的混凝土结构，由于氯离子的侵入使钢筋表面的氯离子浓度达到临界浓度而导致钢筋锈蚀，从而影响到混凝土结构的耐久性和安全性，因此，预测氯离子在混凝土中的浓度分布是评价混凝土结构服役寿命的一个重要环节。虽然氯离子侵入混凝土包括了扩散作用、渗透作用、电化学迁移等综合因素的结果，但在实际的应用中通常认为扩散起主导作用，并采用基于Fick第二定律的氯离子扩散模型进行分析。余红发等［1－3］提出了能同时考虑氯离子的结合能力、氯离子扩散系数的时间依赖性和结构微缺陷影响的混凝土结构服役寿命解析模型；Tang等［4］讨论了使用过于简单的数学解分析混凝土服役寿命可能带来的误差，并给出了一个改进的解析分析方法。虽然解析方法计算量少，使用简单，但由于解析解常受到规则边界条件和材料均匀性的局限，所以实际上常常需要借助于有限元等数值方法。Han［5］考虑结合氯离子和蒸发水对氯离子扩散系数的影响，利用有限元方法分析了混凝土中氯离子浓度的分布；Var Dimitri等［6］应用有限差分法对氯离子引起混凝土中钢筋腐蚀的初始时间进行了评估。杨绿峰等［7］提出了氯离子扩散场的计算长度，并据此建立了混凝土中氯离子扩散分析的补偿长度理论［8］及服役寿命分析的边界元法［9］。有限元法适应性强，但在计算过程中通常在时间域和空间域中需要同时采用细密离散网格，计算量较大、效率不高。边界元法的未知量仅存在于边界结点上，可以使待求解问题的维数降低一维，未知量较少，计算效率得到很大提高。

使用边界元法解决瞬态扩散问题时，可采用与时间相关［7，9］及与时间不相关［11］2种基本解。杨绿峰［7］和郭力［12］分别采用与时间相关和与时间不相关的基本解建立了混凝土中氯离子扩散分析的边界元法。前者可以用较少的时间步得到精度较高的计算结果［8］，所以更适合于在氯离子扩散分析中应用，而且可以选择采用2种不同的时间进程解决时域积分问题［13］：分时段逐步推进法和全时域初值推进法，前者将时间域离散后逐段建立边界元法计算格式，并以前一时间段的计算结果作为下一时间段的初始值；后者总是从初始时刻开始积分，不需要对每个时间步的结果求域内积分，保证了边界元法计算模型仅在扩散域边界上离散，提高计算效率［14］。

本文采用与时间相关的基本解，并利用氯离子扩散场补偿长度理论［8］建立了混凝土中氯离子扩散分析的边界元法，分别利用分时段逐步推进法和全时域初值推进法作为边界元法的时间进程，比较了2种时间进程在氯离子扩散问题中的特点，结果表明：基于全时域初值推进法建立混凝土中氯离子扩散分析的边界元法，可以避免分时段逐步推进法在氯离子扩散域内产生的积分项和域内积分问题，从而简化计算格式，显著提高计算效率，而且能够保证边界元模型中时间域离散网格和计算格式的收敛性，提高计算结果的稳定性。在此基础上，进一步研究了混凝土结构的服役寿命，分析了氯离子扩散维数对混凝土结构腐蚀过程与服役寿命的影响。

1 混凝土中氯离子扩散分析的边界元法

基于Fick第二定律的二维扩散方程可以表示为：

其边界条件和初始条件为：

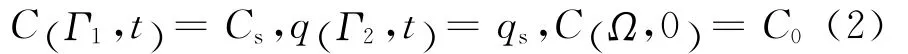
式中：C为混凝土中氯离子浓度（%，氯离子质量占混凝土质量的百分比，本文中氯离子浓度均为此单位）；q为氯离子的浓度梯度，是C的方向导数；t为混凝土暴露于氯离子环境中的时间（a）；D为混凝土中氯离子扩散系数（mm2／a）；Cs、qs分别为混凝土表面氯离子浓度、浓度梯度；C0为混凝土内部初始氯离子浓度；Γ1、Γ2和Ω分别为混凝土的第一、二类边界和域内。

将混凝土中氯离子扩散的时间域［t0，tn］离散成n个子域［tk－1，tk］，（k＝1，2，…，n），且：

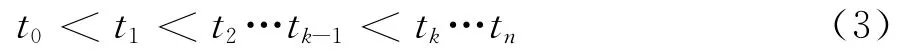
依据文献［7］，可以针对时间子域 ［tk－1，tk］，将式（1）转化为如下积分方程：

式中：AP为与源点P点位置有关的系数，当点P位于氯离子扩散域内部时，AP＝1，反之，当源点P位于扩散域边界上时，AP＝，此时β表示扩散域边界上P点两侧切线的内夹角；为tk时刻混凝土中源点P处的氯离子浓度；C＊、q＊是氯离子扩散问题的基本解［7］。

可以看出，式（4）中每一项积分的起始点都是时间子域的初始时刻tk－1，并将前一个时间子域的计算结果作为该子域的初始值，属于分时段逐步推进法。由于等号右侧第二项属于域内积分，因而该边界元模型通常需要开展域内离散，不仅增加计算量，而且有可能导致计算误差积累，降低计算精度，消减了边界元法的优势。

2 全时域初值推进的氯离子扩散分析边界元法

为了克服分时段逐步推进法存在的问题，这里采用全时域初值推进法建立混凝土中氯离子扩散分析的边界元法模型，即总是从氯离子扩散的时间域［t0，tn］的初始时刻t0开始，对于时域中的任意时刻tk，可建立边界积分方程：

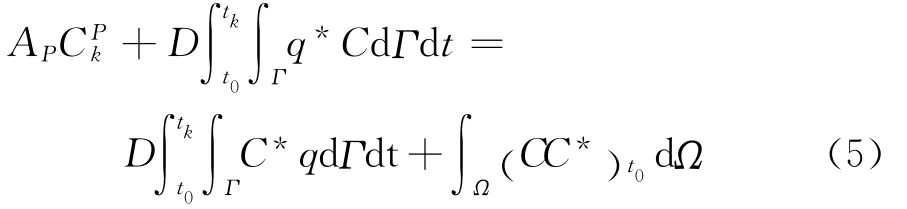
上式等号右侧的域内积分项只存在于时间域的初始时刻t0，为了避免域内离散，需要消除该项，此时可以利用

代替式（1）、（2）中的氯离子浓度C，建立混凝土中氯离子扩散分析的控制方程及其边界条件和初始条件：

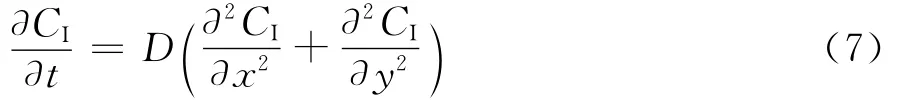
其边界条件和初始条件为：

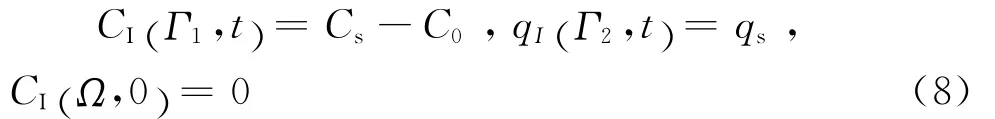
根据上述两式，可以建立关于CI的氯离子扩散分析的边界积分方程：

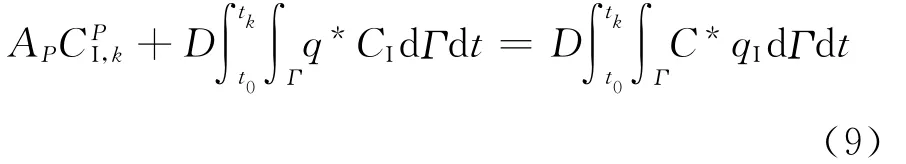
如此即可消除积分方程中的域内积分项，从而充分发挥边界元法的优势。

在式（9）基础上，建立混凝土中氯离子扩散分析的边界元法计算模型。首先根据补偿长度理论［8］确定计算模型的几何尺寸，并沿该模型的边界离散出N个线性单元，同时将氯离子扩散的时间域［t0，tn］离散成n个等步长子域，可得边界元法控制方程：

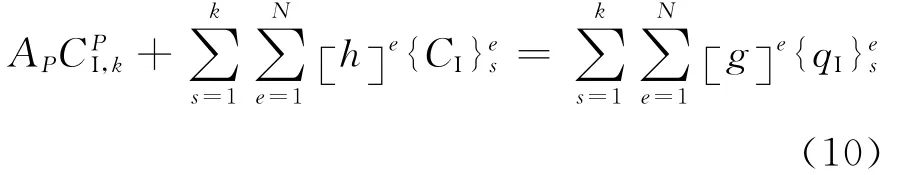
式中，｛CI和 ｛qI分别表示ts时刻单元结点上的氯离子浓度CI及其梯度qI。

其中，［N］＝ ［N1N2］表示单元形函数矩阵；C和q分别由C＊和q＊在时间子域上积分得到：

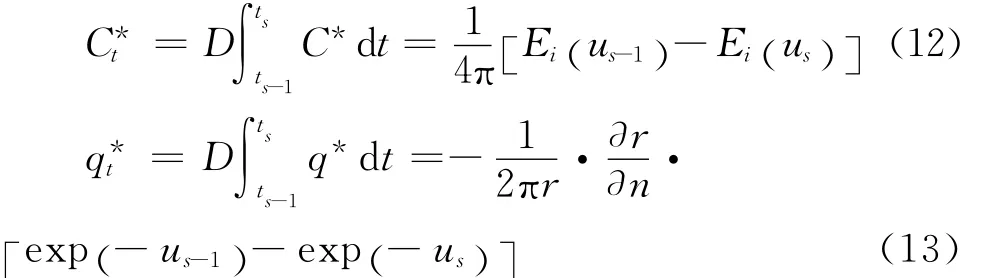
这里：

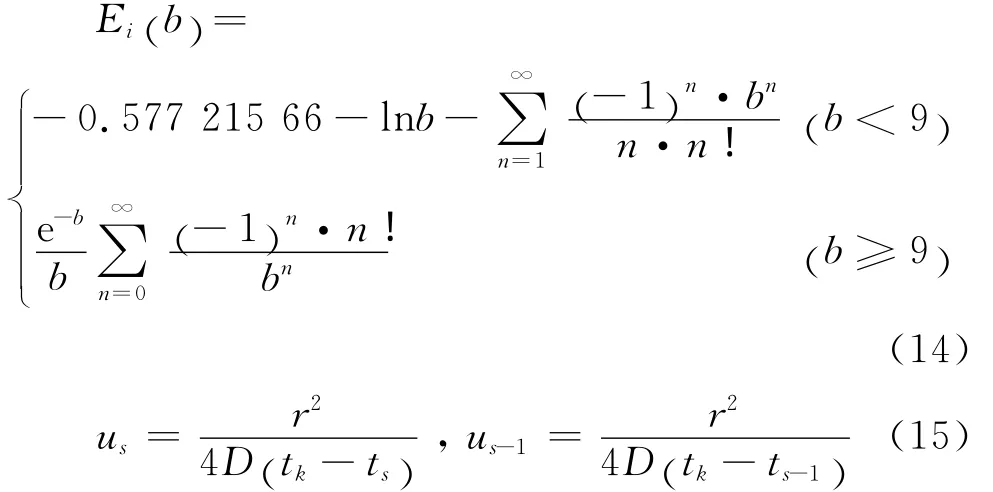
将各边界单元的控制方程集成总体方程，据此可求得边界上各结点处的CI和qI，进而可得到域内点的氯离子浓度值。

3 氯离子侵蚀下混凝土结构服役寿命分析的边界元法

处于氯盐环境下混凝土结构的服役寿命是指结构建成开始使用到结构失效的时间过程，包括诱导期、发展期和失效期3个时期。其中，诱导期是指混凝土内钢筋表面氯离子浓度达到临界值所需的时间；发展期是指从钢筋锈蚀到混凝土保护层胀裂所需的时间；失效期是指从保护层开裂到结构失效所需的时间。文献中通常将诱导期作为氯盐环境下钢筋混凝土结构的服役寿命［9］，而将发展期和失效期作为结构的安全储备。因此这里将诱导期寿命近似视为混凝土结构的服役寿命。

根据混凝土结构中钢筋腐蚀的阈值浓度Ccr和钢筋表面某点 （xd，yd）处t时刻的氯离子浓度C（xd，yd，t），可以建立混凝土结构腐蚀的极限方程：

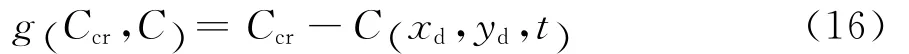
当g （Ccr，C）＝0，即C（xd，yd，T）＝Ccr时，钢筋开始锈蚀，称T为氯盐腐蚀下混凝土结构的服役寿命。

4 算例分析

算例1：使用文献［7］中的算例，边长为1 000mm的钢筋混凝土方板，厚度为100mm，将其中的4个面用环氧树脂封闭，沿厚度方向留下2个相邻面AB和AD暴露在含氯离子的溶液中，如图1所示。混凝土的2个暴露面上的表面氯离子浓度Cs＝1%，初始氯离子浓度为0，混凝土的氯离子扩散系数D为1.0×10－12m2／s。分别采用文献［7］和本文中2种时间进程的边界元法格式计算混凝土板内部对角线处的氯离子浓度，并比较2种时间进程对计算结果的影响。

计算扩散时间分别为10a、30a时混凝土中的氯离子浓度，根据混凝土中氯离子扩散分析的补偿理论［7－8］，边界元计算模型的长度Lt：

扩散时间为10、30a时的补偿长度分别取为L10＝70mm、L30＝110mm，两者都小于构件的实际长度，这里取计算长度建立边界元法计算模型，利用全时域初值推进边界元法计算混凝土板对角线AC上的氯离子浓度值。计算模型中，时间域被均匀划分为5个子域。为了分析模型的收敛性，将模型的全部边界分别离散为8、16和32个等长度单元，并将计算结果与有限元相比较，有限元模型的离散网格为10mm×10mm，时域离散步长为Δt＝0.5a。结果如图2所示。从中可以看出，全时域初值推进边界元法计算结果与有限元法吻合良好，将边界离散为16个边界单元时即可获得较好的计算精度。

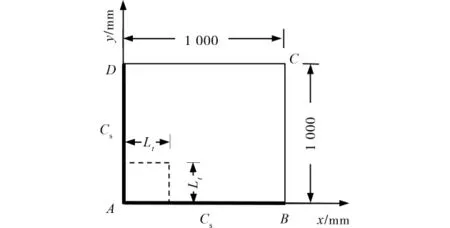
图1 氯离子二维扩散计算模型

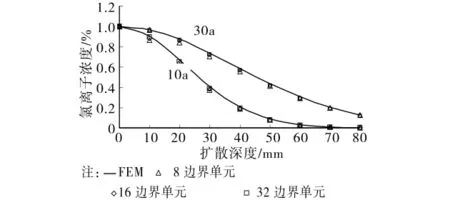
图2 离散边界元数量对计算结果的影响

为了对比全时域初值推进法和分时段逐步推进法对边界元法计算结果和计算效率的影响，这里分别利用两种时间进程方法计算扩散时间为30a时，混凝土板对角线AC上坐标为（40mm，40mm）处的氯离子浓度，并根据有限元法结果分析计算精度和计算效率。2种方法取同样的BEM离散模型，即将边界离散为16个边界单元。另外，由于分时段逐步推进法含有域内积分项，需将扩散域离散为10mm×10mm的域内单元，并采取高斯积分的方法加以处理。计算结果如图3、表1所示，从中可以看出时间域划分的时段数量对2种方法计算结果的精度和效率有明显影响。对于全时域初值推进法，边界元法计算用时少，且计算结果随着时段数量的增加而快速收敛。而分时段逐步推进法耗时随着时段数量的增加而显著增加，而且在时段不超过5个时，计算结果快速向有限元结果靠近，但当时域离散的时段继续增加时，误差反而快速增大，计算结果不收敛。

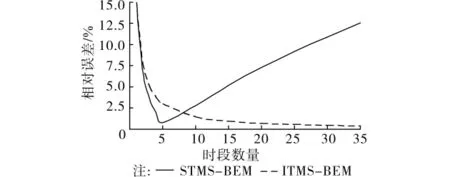
图3 2种时间进程的计算精度比较

表1 2种时间进程的计算耗时比较

根据对BEM模型的分析，分时段逐步推进法产生误差的原因在于式（4）右侧第2项的域内积分。采用常规的高斯积分法计算域内积分时，由于该积分核函数C＊在源点处的值会随着时段增加、时间步长减小而迅速增大。扩散系数D取单位值时，C＊值在源点附近的值如图4所示，从中可以看出，积分核函数在源点处的值随着时间步长的减小而快速增大，且增大部分主要集中在源点附近很小的区域内，造成函数曲线越来越不光滑，从而导致常规的高斯积分法产生误差。此时，即便增加积分点，也难以有效提高计算精度，如图5所示。

尽管可以采取细分域内离散网格或强行令积分核函数在源点处的值为零［10］等方法解决该问题，但前者会弱化边界元法不需要域内离散的优点，增大计算工作量；后者并没有全面解决核函数在源点附件区域过分增大的问题。

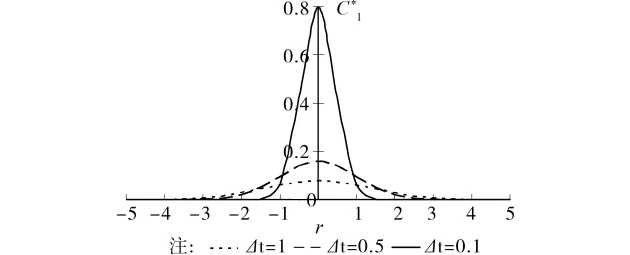
图4 取不同时间步长时的基本解特征

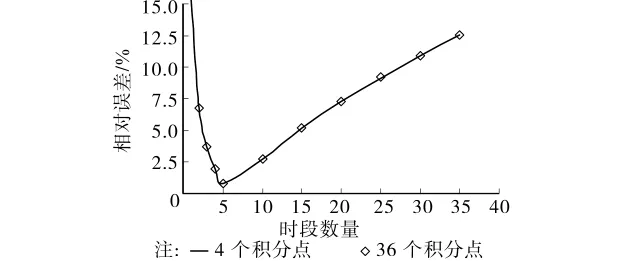
图5 取不同高斯积分点个数对相对误差的影响

算例2 考虑一个截面尺寸500mm×500mm的方形截面混凝土柱，其钢筋配置情况如图6所示，钢筋的保护层厚度为40mm。混凝土柱的4个侧面都暴露于氯盐环境中，设混凝土柱表面氯离子浓度Cs＝0.8%，初始氯离子浓度0，临界氯离子浓度为0.22%［15］，混凝土扩散系数为1.0×10－12m2／s。这里采用本文建立的全时域初值推进边界元法预测该混凝土柱的服役寿命。

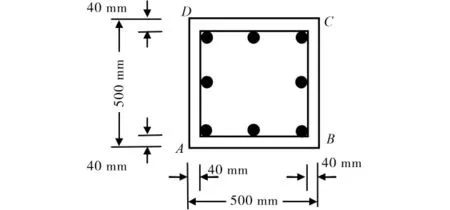
图6 混凝土柱截面及配筋

在柱的角部存在氯离子二维扩散现象，所以可以从角部取出一个边长为Lt＝140mm的混凝土试块，建立边界元法计算模型，其中Lt为计算长度，按照50a结构服役时间和式（17）确定，氯离子沿AE边、AF边进入混凝土试件内，如图7（a）所示；而在远离拐角的中部将发生氯离子一维扩散，因此从边中部取出长度为Lt＝140mm的混凝土试块，建立边界元法计算模型，氯离子沿GH边进入混凝土试件内，如图7（b）所示。这里利用全时域初值推进边界元法计算两个模型中钢筋周围的氯离子浓度，并和有限元法计算结果相比较，结果如图8所示。有限元法计算模型中，氯离子扩散域采用10mm×10mm的离散单元网格，采用Δt＝0.5a的步长离散时域；边界元法计算模型中，全部边界离散为40个等长单元，并采用和有限元法相同的时域离散方式。从图8可以看出，本文建立的全时域初值推进边界元法与有限元计算结果基本吻合，具有较高的计算精度。而且，尽管二个模型中钢筋与构件表面的距离都是40mm，但氯离子浓度及其随时间变化的规律有明显区别，二维扩散区钢筋表面的氯离子浓度明显高于一维扩散区，而且随着扩散时间的增长，二者之间的差别逐渐增大。

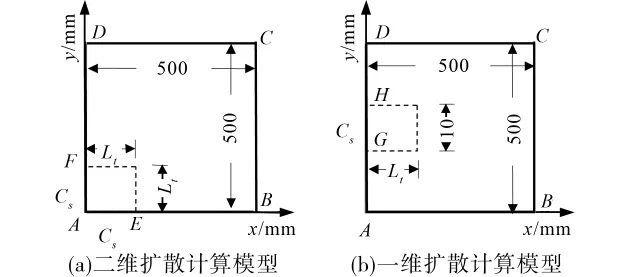
图7 混凝土柱中氯离子扩散计算模型

图8 一、二维扩散条件下钢筋表面的氯离子浓度

根据式（16），利用全时域初值推进边界元法分别计算了一维、二维扩散区钢筋锈蚀时混凝土柱的服役寿命，并将计算结果与有限元法相比较，详见图9。图中结果再次表明，本文方法与有限元法结果基本吻合，具有很高的计算精度。而且可以看出，二维扩散条件下，混凝土结构的服役寿命较一维扩散条件大大降低，因此实际设计中，采用二维氯离子扩散模型进行计算更符合真实情况，才能保证钢筋混凝土结构的耐久性。

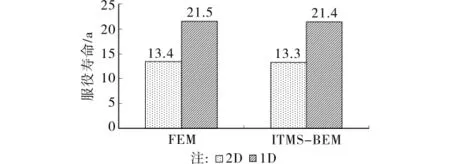
图9 混凝土柱的服役寿命预测值

5 结 语

建立了混凝土中氯离子扩散分析的全时域初值推进边界元法，研究了分时段逐步推进边界元法计算结果不随时域细分而收敛的原因。与分时段逐步推进边界元法相比，全时域初值推进边界元法可以消除氯离子扩散域内的积分项，避免域内离散，不仅简化了计算格式，而且提高了迭代过程的稳定性和计算结果的精度，减少了计算耗时。研究结果表明，氯离子扩散维数对氯离子浓度分布和混凝土结构服役寿命有显著影响，应在结构设计中加以考虑。

［1］余红发，孙伟，鄢良慧，等.混凝土使用寿命预测方法的研究I—理论模型［J］.硅酸盐学报，2002，30（6）：686－690.Yu H F，Sun W，Yan L H，et al.Study on prediction of concrete servive life I－theoretical model［J］.Journal of the Chinese Ceramic Society，2002，30（6）：686－690.

［2］余红发，孙伟，鄢良慧，等.混凝土使用寿命预测方法的研究II—模型验证与应用［J］.硅酸盐学报，2002，30（6）：691－695.Yu H F，Sun W，Yan L H，et al.Study on prediction of concrete service life II －model's examination and application ［J］.Journal of the Chinese Ceramic Society，2002，30（6）：691－695.

［3］余红发，孙伟，鄢良慧，等.混凝土使用寿命预测方法的研究III—混凝土使用寿命的影响因素及混凝土寿命评价［J］.硅酸盐学报，2002，30（6）：696－701.Yu H F，Sun W，Yan L H，et al.Study on prediction of concrete service life III －evaluation of influencing factors and service life ［J］.Journal of The Chinese Ceramic Society，2002，30（6）：696－701.

［4］Tang L P，Joost G.On the mathematics of timedependent apparent chloride diffusion coefficient in concrete［J］.Cement and Concrete Research，2007，37（4）：589－595.

［5］Han S H.Influence of diffusion coefficient on chloride ion penetration of concrete structure［J］.Construction and Building Materials，2007，21：370－378.

［6］Var Dimitri V，Trapper P A.Probabilistic evaluation of initiation time of chloride induced corrosion ［J］.Reliability Engineering ＆ System Safety，2008，93：364－372.

［7］杨绿峰，陈正，王燚，等.混凝土中氯离子二维扩散分析的边界元法［J］.硅酸盐学报，2009，37（7）：1110－1117.Yang L F，Chen Z，Wang Y，et al.Boundary element method for analysis of two－dimensional chloride diffusion in concrete［J］.Journal of the Chinese Ceramic Society，2009，37（7）：1110－1117.

［8］杨绿峰，陈正，刘鸿亮，等.混凝土中氯离子时变扩散的边界元分析［J］.土木建筑与环境工程，2011，33（4）：73－79.Yang L F，Chen Z，Liu H L，et al.Boundary element method for time－dependent chloride diffusion and the chloride distribution in concrete ［J］.Journal of Civil，Architectural ＆ Environmental Engineering，2011，33（4）：73－79.

［9］陈正，杨绿峰，冯庆革，等.高性能混凝土的氯离子扩散及服役寿命研究［J］.建筑材料学报.2010，13（2）：222－227.Chen Z，Yang L F，Feng Q G，et al.Study of chloride diffusion of high－performance concrete and its service life by the boundary element method ［J］.Journal of Building Material，2010，13（2）：222－227.

［10］Mohammadi M，Hematiyan M R，Marin L.Boundary element analysis of nonlinear transient heat conduction problems involving non－homogenous and nonlinear heat sources using time－dependent fundamental solutions［J］.Engineering Analysis with Boundary Elements，2010，34：655－665.

［11］Singh K M，Kalra S.Time integration in the dual reciprocity boundary element analysis of transient diffusion ［J］.Engineering Analysis with Boundary Elements，1996，18：73－102.

［12］Guo L，Chen T，Gao X W.Transient meshless boundary element method for prediction of chloride diffusion in concrete with time dependent nonlinear coefficients［J］.Engineering Analysis with Boundary Elements，2012，36：104－111.

［13］Feng Z X，Tang S W，Li Z X.A new time marching BE scheme for transient heat transfer with a thermal moving boundary ［J］.Engineering Analysis with Boundary Elements，1998，22：71－75.

［14］Wrobe L C，Aliabad M H.The boundary element method：applications in thermo－fluids and acoustics［M］.Chichester：Johu Wiley＆Sons，2002.

［15］王晓舟，金伟良，金立兵.基于广义扩散方程海工混凝土结构耐久寿命概率评估方法［J］.海洋工程.2009，27（3）：85－90.Wang X Z，Jin W L，Jin L B.A probabilistic approach of life prediction of marine concrete structures based on GDF［J］.The Ocean Engineering，2009，27（3）：85－90.