考虑初应力的钢管混凝土柱轴压承载力统一解
李 艳,赵均海,梁文彪,王 苏
(长安大学 建筑工程学院,西安710061)
钢管混凝土具有承载力高、施工方便、塑性、耐火性能和经济效果好等优点,并随着研究理论的不断深入和完善[1-5],已被广泛应用于多高层建筑大直径柱、海洋平台、桥梁拱肋和桥墩等结构中。然而,实际施工中,通常是先安装若干层空钢管,再在空钢管中浇灌混凝土,因此,钢管在和混凝土共同受力之前,由于施工荷载和湿混凝土自重等因素,产生了纵向初压应力[6]。钢管初应力的存在占有了部分钢管承载力,将影响钢管和核心混凝土共同受力阶段的开始和终了。因此,研究初应力对钢管混凝土构件力学性能的影响,是学者一直关注的热点问题之一,对合理地确定钢管混凝土构件极限承载力具有重要意义。
虽然目前世界各国规程大都没有合理的反映初应力对钢管混凝土构件受力性能的影响和计算方法[6-8],但各国学者都进行了许多研究:韩林海[6]对有初应力的方钢管混凝土压弯构件进行了试验研究和有限元分析,得到了有初应力影响的钢管混凝土压弯构件承载力的实用验算方法;陈宝春等[9-12]采用有限元方法对钢管初应力作用下的钢管混凝土柱进行了数值分析,提出了相应的极限承载力计算公式;周水兴等[13-16]对钢管混凝土拱桥进行了试验研究和有限元分析,得到了钢管初应力对钢管混凝土拱桥力学性能的影响等。这些研究成果为该课题的深入研究提供了宝贵的试验数据和理论依据,然而仍存在一定的不足:1)研究方法大多为数值分析方法和极限平衡法,没有较合理的破坏准则为基础;2)初应力影响系数的计算公式大多由试验曲线或数值模拟曲线拟合而得,缺乏理论基础;3)计算过程和计算公式较复杂,不便工程实用。
本文采用双剪统一强度理论,对有初应力的钢管混凝土轴压短柱力学性能进行分析,引入考虑长细比影响的折减系数,建立了钢管初应力影响下钢管混凝土柱轴压极限承载力的统一解。在此基础上,推导出一个新的基于统一强度破坏准则的初应力影响系数,并对其各参数进行了分析。
1 双剪统一强度理论
双剪统一强度理论[17]考虑了中间主应力和材料拉压比的影响,能够适用于各类不同的材料,其表达式为
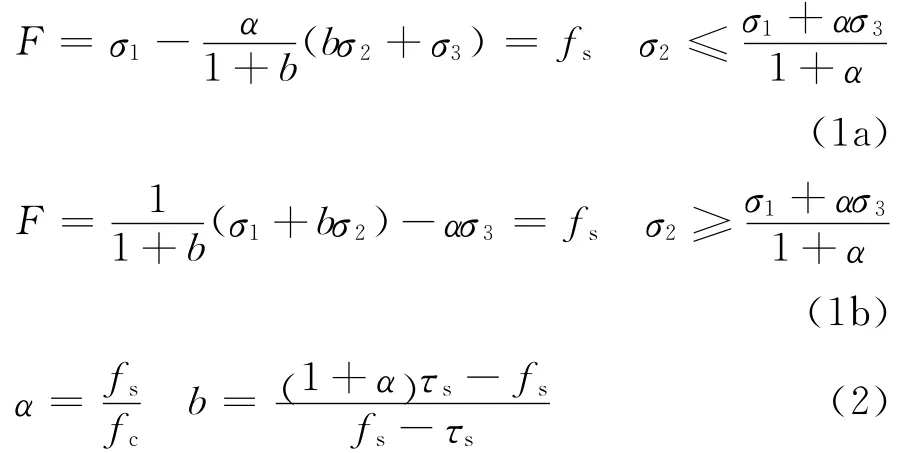
式中:σ1、σ2和σ3分别为第一、第二和第三主应力;α为材料的拉压比;fs、fc和τs分别材料的拉伸屈服应力、压缩屈服应力和剪切屈服应力;b是加权系数,同时也是选用不同强度准则的参数,反映了中间切应力及相应作用面上的正应力对材料屈服或破坏的影响,0≤b≤1。
2 考虑初应力的钢管混凝土柱轴压极限承载力
设钢管混凝土柱外径为D,核心混凝土的直径为d,钢管的厚度为ts,对核心混凝土提供的侧向约束力为σr,钢管所受的环向拉应力为σθ,轴向压应力为σz,初应力为σ0。当σ0=0时,为不考虑初应力的钢管混凝土柱。钢管与核心混凝土受力简图如图1所示。

图1 钢管与核心混凝土受力简图
2.1 考虑初应力的钢管混凝土短柱轴压极限承载力
1)钢管应力分析
由图1(a)可得

钢管在轴压、环拉和径向受压的三向应力状态下屈服时,环向应力增大,纵向承载力有所降低,径向压应力较小[1]。若规定σ1≥σ2≥σ3,则
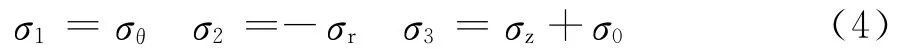
因为
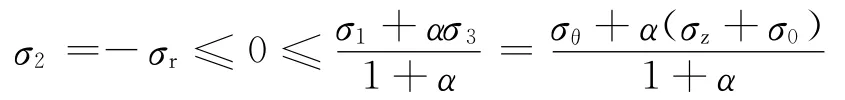
故将式(4)代入式(1a)得
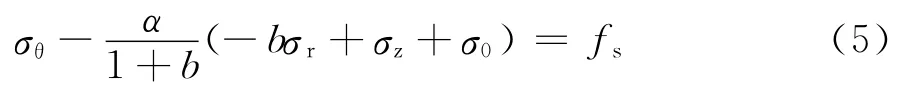
将式(3)代入式(5),整理可得
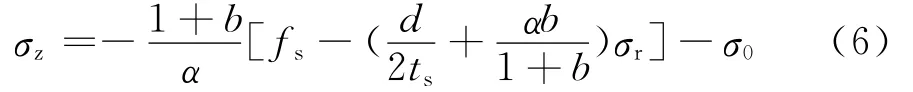
2)核心混凝土应力分析
对于核心混凝土,其受力状态为0≥σ1=σ2≥σ3,由统一强度理论推得[17]

但对受压混凝土,一般取压为正拉为负,则上式变为

式中:σ3为核心混凝土抗压强度;fc为混凝土圆柱体抗压强度为混凝土的内摩擦角,k取值在1.0~7.0之间,具体由试验确定。
假定钢管和混凝土径向变形协调,由图1可得

将式(8)代入式(7)得

3)考虑初应力的钢管混凝土短柱轴压极限承载力
钢管混凝土短柱轴压承载力由钢管的承载力和核心混凝土的承载力共同组成,即

式中:Ac为核心混凝土的横截面积,As为钢管的横截面积,且

将式(6)、(9)和(11)代入式(10),整理可得

由

得

将式(13)代入式(12),则考虑初应力的钢管混凝土短柱轴压极限承载力为
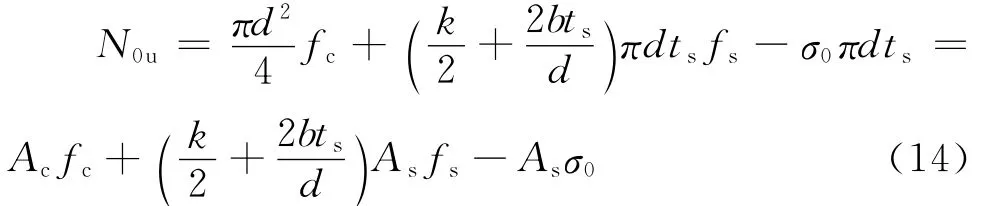
初应力的大小用初应力度β表示,且

式中:φ为空钢管构件轴心受压稳定系数,按《钢结构设计规范》(GB 50017-2003)中的有关规定确定。设截面的含钢率η=,套箍系数ξ=,则式(14)可以简化为

2.2 考虑初应力和长细比影响的钢管混凝土柱的轴压极限承载力
引入考虑长细比影响的稳定系数φl[18],且取
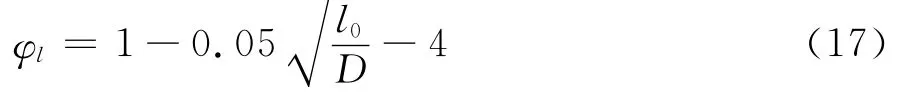
式中:l0为计算长度,取l0=μl。
则考虑钢管初应力和长细比影响的钢管混凝土柱的轴压极限承载力为
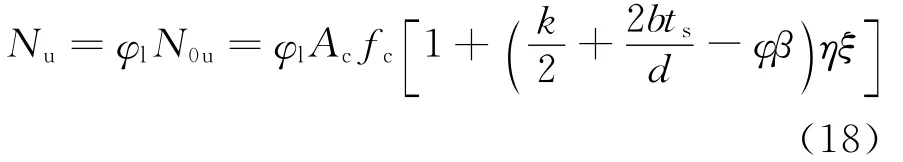
2.3 不考虑初应力的钢管混凝土柱轴压极限承载力
当β=0,φl=1时,式(18)退化为不考虑初应力的钢管混凝土短柱轴压极限承载力的计算公式,即

当β=0,φl≠1时,式(18)退化为不考虑初应力的钢管混凝土长柱轴压极限承载力的计算公式,即

其中,k为材料影响系数,与混凝土的内摩擦角θ有关,文献[1]取4,θ=34.42°,文献[19]取3.6,θ=36.87°。
当k=4,b=0时,式(20)可简化为

与文献[1]中的计算公式完全一致。
3 计算实例及影响因素分析
根据文献[20]提供的钢管混凝土轴压构件的试验资料和数据,采用公式(18)计算其极限承载力,将计算结果和试验结果进行比较,比较结果见表1。

表1 计算结果和文献[20]试验结果对比(k=3.6)
从表1中可知,由本文公式计算得到的理论值与试验值吻合良好,验证了公式的合理性。当长细比λ一定时,钢管混凝土轴压构件极限承载力随初应力度β的增大而降低;当初应力度β一定时,其极限承载力随长细比λ的增大而降低。这表明,虽然初应力的存在可以延缓构件的破坏[6,10],但这种延缓作用并不能阻止构件的极限承载力随构件长细比λ的增大而降低的趋势,因为当长细比λ较大,构件破坏形态为稳定破坏,而非强度破坏,长细比λ的影响大于初应力等其他因素的影响,占主导地位。
图2给出了文献[20]试件的试验值和采用本文公式计算所得的理论值在有无初应力状态下,随加权系数b和长细比λ的变化趋势。
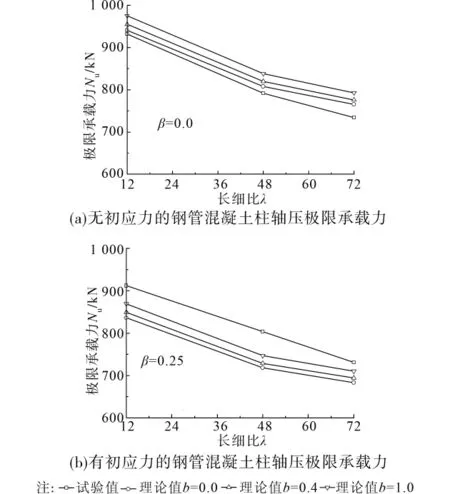
图2 钢管混凝土柱轴压极限承载力影响因素分析
由图2可以看出,当考虑钢管初应力的影响时,钢管混凝土柱的轴压极限承载力Nu有所降低,并且,由本文公式计算所得的理论值与试验值相比偏于安全。另外,由图2还可看出,当初应力度β一定时,Nu随加权系数b的增大而增大,随长细比λ的增大而减小。这一结论与试验结果一致。
4 初应力影响系数及参数分析
4.1 初应力影响系数
设初应力影响系数为φβ,则
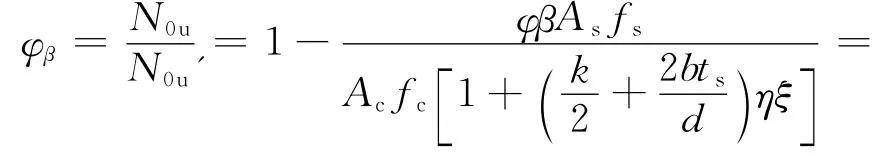

式中:N0u、N0u'分别为考虑初应力影响和不考虑初应力影响的钢管混凝土轴压短柱极限承载力。
由上述分析可知,初应力影响系数φβ是根据统一强度破坏准则建立的,与以往拟合试验曲线或数值模拟曲线的方法不同。φβ较全面地体现了初应力度β、构件长细比λ(空钢管稳定系数φ)、截面含钢率η、套箍系数ξ、钢材屈服强度fs、混凝土强度fc和材料影响系数k等多种因素的影响。
4.2 可行性比较
图3给出了本文推导出的初应力影响系数φβ与文献[6]、[9]和[10]中的初应力影响系数kp的比较,计算条件为D=108mm,e/r=0,0≤β≤0.6,η=0.16,ξ=14.55,Q345钢材,C50混凝土,k分别取4,5,6,7。b是选用不同强度准则的参数,当b=0时,为Mohr-Coulomb强度准则;当b=1时,为双剪强度理论;当α=1,b=0,0.5和1时,则分别为Tresca屈服准则、Mises屈服准则的线性逼近及双剪屈服准则。此处取b=1,即取双剪屈服准则下的初应力影响系数φβ与相关文献中的初应力影响系数进行比较。
由图3可见,本文推导出的初应力影响系数与文献资料中的初应力影响系数相比,偏于安全,具有一定的可行性。同时,图3还表明,k取值越大,本文推导出的初应力影响系数与文献资料中的初应力影响系数吻合越好,并且,λ越大,吻合越好。这是由于本文偏安全地考虑了初应力对钢管混凝土柱轴压极限承载力的影响。
4.3 参数分析
根据式(22)对影响初应力系数φβ的各参数进行分析。计算条件为D =108mm,ξ=14.55,e/r=0,0≤β≤0.6,b=1,对于k,参考文献[19],取k=3.6。
1)初应力度β和长细比λ
当η=0.16,Q345钢材,C50混凝土时,在不同长细比λ影响下,初应力影响系数φβ随初应力度β的变化规律如图4所示。
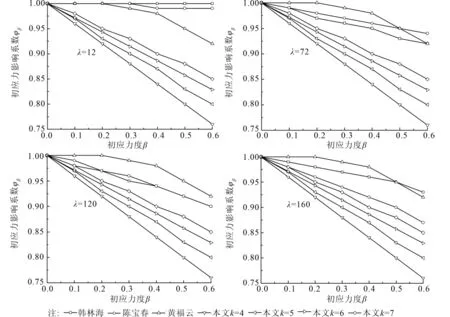
图3 本文与相关文献初应力影响系数φβ比较
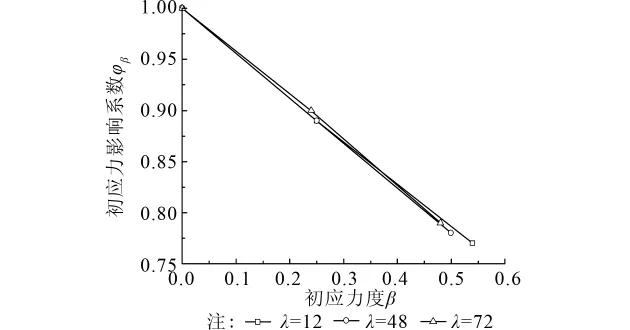
图4 不同λ下,φβ随β的变化规律
图4 表明,当构件长细比λ等其他因素一定时,φβ随初应力度β的增大而减小。这是因为,钢管初应力的存在占有了钢管承载力的一部分,将影响钢管和核心混凝土共同承受的极限荷载,且初应力越大,这种影响越显著。另外,图4还表明,当初应力度β较小时,φβ随构件长细比λ的增大(即φ的减小)而增大,这是因为,当构件长细比λ较大时,钢管混凝土构件跨中截面受拉区域较大,钢管初压应力的存在延缓了截面受拉区域的发展,从而延缓了构件的破坏;当初应力系数β较大时,φβ随构件长细比λ的增大(即φ的减小)而减小,这是因为,长柱较短柱对初应力更为敏感,随初应力度β的增大下降速度更快。
2)初应力度β和钢材屈服强度fs
当η=0.16,λ=72,C50混凝土时,在不同钢材屈服强度fs影响下,初应力影响系数φβ随初应力度β的变化规律如图5所示。
图5表明,φβ随钢材屈服强度fs的增大而减小。这是因为,钢材屈服强度fs越高,钢管承载力占钢管混凝土构件承载力的比重越大,钢管初应力的影响越显著,同文献[6]结论一致。
3)初应力度β和混凝土强度fc

图5 不同fs下,φβ随β的变化规律
当η=0.16,λ=72,Q345钢材时,在不同混凝土强度fc影响下,初应力影响系数φβ随初应力度β的变化规律如图6所示。
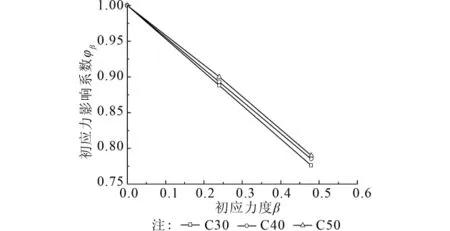
图6 不同fc下,φβ随β的变化规律
图6 表明,φβ随混凝土强度fc的增大而增大。这是因为,混凝土强度fc越高,核心混凝土承载力占钢管混凝土构件承载力的比重越大,钢管承载力比重越小,钢管初应力的影响越不显著,同文献[6]结论一致。图6还表明,混凝土强度fc对初应力影响系数φβ的影响不大,研究表明[6],在工程常用参数范围内,混凝土强度对初应力影响系数的影响在1%左右变化。
4)含钢率η和套箍系数ξ的影响规律
含钢率η和套箍系数ξ对初应力影响系数φβ的影响规律同钢材屈服强度fs,即φβ随含钢率η和套箍系数ξ增大而减小。这是因为,含钢率η和套箍系数ξ越大,钢管承载力占钢管混凝土构件承载力的比重越大,钢管初应力的影响越显著。
图7为当λ=72,Q345钢材,C50混凝土时,在不同含钢率η影响下,初应力影响系数φβ随初应力度β的变化规律。

图7 不同η下,φβ随β的变化规律
5 结 论
1)采用双剪统一强度理论,考虑中间主应力和材料拉压比的影响,建立了考虑初应力影响的钢管混凝土柱轴压极限承载力的统一解,计算值与试验值吻合良好,验证了公式的合理性,也说明了统一强度理论对有初应力的钢管混凝土轴压构件具有良好的适用性。
2)研究表明,考虑初应力的钢管混凝土柱的轴压极限承载力,当长细比和和加权系数一定时,随初应力度的增大而减小;当初应力度和长细比一定时,随加权系数的增大而增大;当初应力度和加权系数一定时,随长细比的增大而减小。
3)推导出一个新的基于统一强度破坏准则的初应力影响系数,该系数较全面合理地考虑了长细比、初应力度、套箍作用、含钢率和材料影响系数等多种因素的影响,且偏于安全。
4)对于轴压长柱,在轴压短柱的基础上,引入考虑长细比影响的折减系数,研究表明,该方法简洁合理,便于工程实用。
[1]蔡绍怀.现代钢管混凝土结构[M].北京:人民交通出版社,2003.
[2]Chen B C,Paulo B L.An overview of concrete and CSFT arch bridges in China [C]//Proceedings of the Fifth International Conference on Arch Bridge.Madeira,Portugal,2007.
[3]Sakino K,Nakahara H,Morino S,et al.Behavior of centrally loaded concrete-filled still-tube short columns[J].Journal of Structural Engineering,2004,130(2):180-188.
[4]Nassif A Y.Finite element thermal analysis of concrete filled hollow steel sections during fires [J].Emirates Journal for Engineering Research,2004,9(2):111-115.
[5]Mander J B,Priestley M J N,Park R.Theoretical stress-strain model for confined concrete[J].Journal of Structural Engineering,1988,144(8):1804-1826.
[6]韩林海,尧国皇.钢管初应力对钢管混凝土压弯构件承载力的影响研究[J].土木工程学报,2003,36(4):9-18.Han L H,Yao G H.Effect of initial stress on bearing capacity of concrete-filled steel tubular beam-columns[J].China Civil Engineering Journal,2003,36(4):9-18.
[7]ASCCS.Concrete filled steel tubes-a comparison of international codes and practices[R].ASCCS Seminar Report,Innsbruck,September,1997.
[8]Johansson M,Gylltoft K.Mechanical behavior of circular steel-concrete composite stub columns [J].Journal of Engineering Mechanics,2002,128(8):1073-1081.
[9]陈宝春,黄福云.有初应力的钢管混凝土偏压构件极限承载力计算[J].长沙交通学院学报,2008,24(2):1-8.Chen B C,Huang F Y.Calculation of ultimate loadcarrying capacity of eccentrically loaded concrete filled steel tubular(CFST)columns with initial stresses [J].Journal of Changsha Communications University,2008,24(2):1-8.
[10]黄福云,陈宝春,林友勤,等.初应力对钢管混凝土轴压柱套箍作用影响研究[J].福州大学学报:自然科学版,2011,39(4):575-588.Huang F Y,Chen B C,Lin Y Q,et al.Research on hooping effect of concrete filled steel tube stubs with initial stress under axial compression [J].Journal of Fuzhou University:Natural Science Edition,2011,39(4):575-588.
[11]Xiong D X,Zha X X.A numerical investigation on the behavior of concrete-filled steel tubular columns under initial stress [J].Journal of Construction Steel Research,2007,63(5):599-611.
[12]Xiong D X,Zha X X.Non-linear analysis of the initial stress effect on the behavior of concrete-filled square steel tubular members[C]//Proceedings of the Fourth International Conference on Advances in Steel Structures.Shanghai:Elsevier Science Ltd,2005,599-611.
[13]周水兴,刘琪,陈湛荣.钢管初应力对哑铃型钢管砼拱桥承载力影响分析[J].工程力学,2008,25(7):159-178.Zhou S X,Liu Q,Chen Z R.Effect of initial stress on bearing capacity of dumbbell concrete-filled steel tube arch bridge[J].Engineering Mechanics,2008,25(7):159-178.
[14]韦建刚,黄福云,陈宝春.初应力对钢管混凝土单圆管拱极限承载力影响的研究[J].工程力学,2010,27(7):103-112.Wei J G,Huang F Y,Chen B C.Research on the influence of initial stress to ultimate load carrying capacity of concrete filled steel tubular(single tube)arches[J].Engineering Mechanics,2010,27(7):103-112.
[15]周水兴,张敏,王小松.钢管初应力对钢管砼拱桥承载力影响非线性分析[J].计算力学学报,2010,27(2):291-302.Zhou S X,Zhang M,Wang X S.Nonlinear analysis of steel tube initial stress effect in stell tube on bearing capacity for CFST arch bridges[J].Chinese Journal of Computational Mechanics,2010,27(2):291-302.
[16]Wei J G,Chen B C,Wu Q X,et al.Equivalent beamcolumn method to estimate in-plane circle loads of parabolic fixed steel arches [J].Bridge Engineering,ASCE,2009,14(5):346-354.
[17]Yu M H.Unified strength theory and its applications[M].Berlin:Springer,2004.
[18]赵均海.强度理论及工程应用[M].北京:科学出版社,2003.
[19]谭克锋,蒲心诚,蔡绍怀.钢管超高强混凝土的性能与极限承载力的研究[J].建筑结构学报,1999,2(1):10-15.Tan K F,Pu X C,Cai S H.Study on the mechanical properties of steel extra-high strength concrete encased in steel tubes[J].Journal of Building Structures,1999,2(1):10-15.
[20]黄福云,陈宝春.初应力对钢管混凝土轴压构件受力性能的影响[J].福州大学学报:自然科学版,2008,36(4):272-277.Huang F Y,Chen B C.Influence of initial stress to behavior of concrete filled steel columns under axial loads [J].Journal of Fuzhou University:Natural Science Edition,2008,36(4):272-277.

