悬浮隧道锚索涡激振动影响因素分析

罗 刚，周晓军，王 爽

（西南交通大学 交通隧道工程教育部重点实验室，成都610031）

水中悬浮隧道，其英文名称为Submerged Floating Tunnel，简称SFT，又称 Archimedes桥［1］。顾名思义，这种隧道结构既不位于地层中也不穿过地层，而是悬浮在水面下一定深度，主要依靠自身结构的浮力或支持系统保证其在固定的位置，是一种跨越深水道的新概念。按照支撑方式的不同，悬浮隧道可分类为：下墩立柱式、下锚（锚索）式和水面浮筒式［2］。锚索式悬浮隧道对水下基础的工程地质条件的适应性强，由于其柔性支撑，对地震、海啸等自然灾害的抵御能力强，具有相当广阔应用前景。

锚索类似于海洋工程领域的拖缆、立管和张力腿等柔性海洋结构物，涡激振动（Vortex Induced Vibration，VIV）是此类结构物疲劳损坏的根源，锚索系统的涡激振动分析是悬浮隧道结构分析的重要组成部分。根据aimy线性微幅波理论，波浪力随着水深成指数衰减，悬浮隧道一般置于水下30m左右，此深度锚索的波浪力与水流力相比为微量［3］。因此，本文简化处理只考虑均匀流诱发的漩涡导致锚索动力响应。

随着计算流体力学（CFD）和多场耦合技术的发展，涡激振动的预报模式出现了2个分支：1）基于经验参数模式；2）基于CFD预报模式。前者，流体力系数由系列实验提取，将其按无量纲振幅与折合速度频率整理成数据表，采用样条曲线外推内插的方法拟合为公式，用于VIV的预报。在经验预报模型中，具有代表性的是Harlten和Currie创立的尾流振子模型；基于CFD的VIV研究分为：涡方法［4］，RANS方法［5］，LES方法［6］，以及 DNS法。4类方法的计算量依次增加，对计算机硬件要求越高，精度越高。其中，DNS法由于网格质量要求极高，目前只用于Reynold数低于O（104）的情况，离散涡方法对涡粘模式简化形式决定了其计算精度，更多的研究集中在基于RANS和LES模式流体力系数的求解与结构分析耦合的VIV研究。

对于悬浮隧道锚索涡激振动研究成果主要表现在基于经验参数计算方法，麦继婷等［7］、葛斐等［8］、陈健云等［9］先后采用Morison方程计算锚索的流体力，通过Galerkin法和Hamilton原理求解振动方程，计算锚索涡激振动响应，并未考虑到锚索与流体之间的耦联作用。本文首次将数值模拟方法和多场耦合技术引入锚索涡激振动分析。

1 基本方程和计算模型

1.1 基本方程

1.1.1 流体控制方程 将Naviar－Stokes方程中瞬时变量分解成平均量和脉动量2部分，利用雷诺应力法得到的动量方程和连续性方程如下式：

1.1.2 结构动力方程 锚索动力方程的归一化形式如下：

1.2 计算模型

二维切片法是海洋立管和张力腿涡激振动分析方法，其核心是将三维结构系统简化为多质点的弹簧 质量 阻尼的二维刚性体系。本文将此法引入悬浮隧道锚索的涡激振动分析，锚索等效模型如图1（a）所示。

流场计算采用网格计算区域为20D×40D的矩形，结构中心位于笛卡尔坐标原点，上（下）边界和左边入口边界到结构中心的距离为10D；右边出口边界到结构中心的距离为30D。模型边界条件为：进口采用速度入口边界（inlet）；出口采用自由出流边界（outflow）；上下边界采用自由滑移边界（symmetry）；结构壁面采用无滑移边界（wall），边界条件、网格尺寸和计算区域的大小等无关性验证同Kelkar［11］和Stansby［12］。网格分布为：锚索周围2D范围采用结构化边界层网格，边界层网格相对结构静止且随结构一起振动；远壁面采用可变形的三角形非结构化网格，并利用尺寸函数控制网格的合理分布。近壁面网格如图1（b）所示。流场求解采用RSM湍流模型结合增强壁面函数法。速度与压力耦合方程采用SIMPLEC算法，对流项采用二阶迎风格式。

具体耦合迭代模式为：在某一流场计算时间步Δt内，求解流场控制方程（1）得到锚索壁面压力分布，并将表面压力沿坐标轴投影得到锚索的升力FL（t）和FD（t），采用 UDF（user defined function）编写的四阶Runge－Kutta法嵌入FLUENT求解方程式（3）和（4），得到下一迭代步开始时刻锚索的速度和位移，通过FLUENT中动网格宏DEFINE＿CG＿MOTION将锚索运动速度传递给网格，网格运动导致流场参数改变，进入下一迭代步计算，如此循环反复迭代。

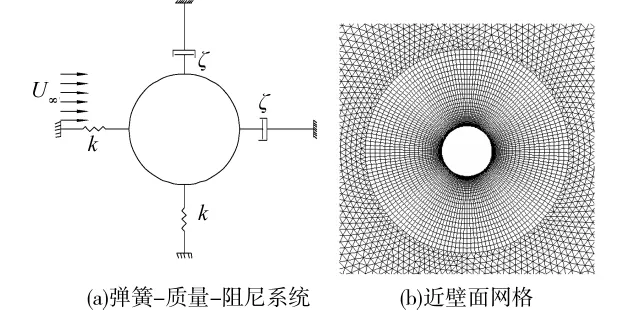
图1 计算模型

2 结果分析

2.1 算法验证

对比各种拟建悬浮隧道方案，选取锚索的主要参数如表2所示。

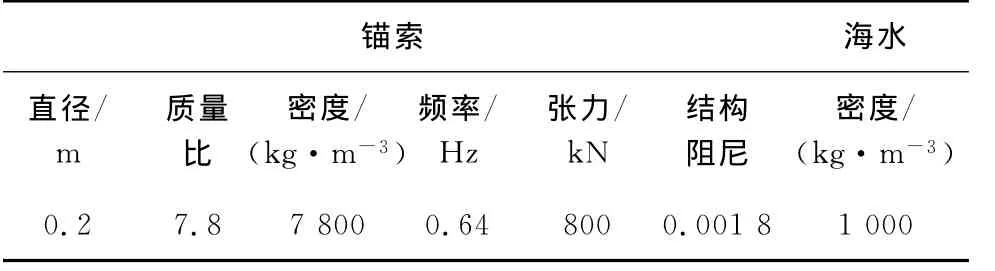
表2 计算参数

根据Feng［13］及 Khalak等［14］的实验，弹性支撑的低质量比刚性柱体的涡激振动幅值随约化速度U＊的增加，表现为初始分支（initial branch）、上端分支（upper branch）和下端分支（lower branch）。为验证本文算法的可行性，图2给出锚索涡激振动的无量纲幅值（Ymax／D）随U＊变化，并与实验结果和其他算法进行比较分析。

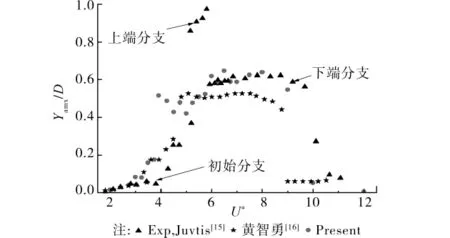
图2 不同约化速度U＊的Ymax／D比较

由图2可知，数值计算无量纲振幅与Juvtis等［15］试验结果在初始分支和下端分子吻合较好，进一步验证本文算法可行性；在约化速度U＊＝6.5时，本文计算下端分支最大振幅为Ymax／D＝0.646，Juvtis等试验结果下端分支最大值为Ymax／D＝0.623，出现在约化速度U＊＝7.8。黄智勇等［16］数值计算结果比本文结果略小。

2.2 质量比影响分析

假定ζ＝0.001 8，保持刚度和直径不变的条件下，通过改变锚索的密度，调整M＊＝2.4、7.8、20时，图3给出了3种质量比锚索涡激振动幅值随约化速度U＊的变化。

从图3可以看出，锚索横向位移最大值（振幅）随着约化速度先增加，之后涡激共振幅值保持在一定范围内，在U＊超过涡激振幅的范围时，锚索涡激振动幅值明显减少。在涡激共振区域，锚索涡激横向振幅随着质量比的变化不是很明显，几乎保持在一定幅值范围内，不同的质量比涡激共振区域不同，质量比M＊＝2.4、7.8和20.0出现涡激共振对应的约化速度范围为：［3.25，11.0］、［4.25，10］和［4.75，10］，质量比越小，涡激共振范围越大，锚索更易发生涡激振动。

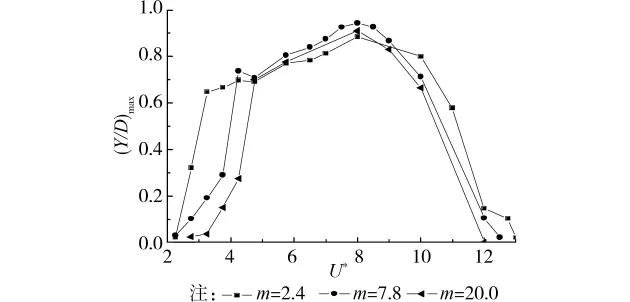
图3 不同约化速度的振幅

图4 给出了约化速度U＊＝5.75时，不同质量比的锚索涡激共振位移时程与频率图。

从图4可看出，3种不同质量比的锚索对应的横向振幅和频率分别为：0.769 9和1.174Hz；0.802 5和0.967Hz；0.778和0.708Hz。由此可知，在涡激共振区域，锚索横向共振频率随质量比的增加而减少，而横向振幅与质量比的关系不是很明显，不同质量比涡激共振时横向振幅大致在［0.76，0.81］。

2.3 阻尼比影响分析

为分析阻尼比对锚索涡激振动的影响，假定M＊＝7.8，ζ＝0、0.001 8、0.018条件下，图5给出了锚索涡激振动幅值随约化速度U＊的变化关系。

从图5可以看出，锚索横向位移最大值（振幅）随着约化速度先增加后减少，当4.25＜U＊＜10.0时，涡激共振幅值保持在一定范围内，在U＊＞10.0时，锚索涡激振动幅值明显减少。在涡激共振区域［4.25，10］，锚索涡激横向振幅随着阻尼比的增加而明显减少，涡激共振区域几乎不随锚索阻尼的变化而改变。

图4 U＊＝5.75锚索横向位移

图5 不同约化速度的振幅

限于篇幅，图6仅给出了约化速度U＊＝7.0时，锚索涡激振动位移随时间的变化关系。

从位移图和频率图可看出，3种不同阻尼比的锚索对应的横向振幅和频率分别为：0.855和1.3Hz；0.821和1.3Hz；0.628 5和0.986Hz。由此可知，在涡激共振区域，锚索横向振幅随阻尼比的增加而减少。比较图6（b）和（c）的频率图可知，随着阻尼比的增加，锚索涡激振动频率由ζ＝0.001 8的1.3Hz下降到ζ＝0.018的0.986Hz，涡激振动周期增加。

图6 U＊＝7.0锚索横向位移

2.4 自由度影响分析

早期对高质量比的涡激振动研究中通常不考虑流向运动对横向振动的影响。但是，在低质量比的情况下，流向运动对横向振动的影响不可忽略。Sarpkaya［17］通过对质量比为7.0的两自由度（横流向和顺流向）圆柱体涡激振动的实验研究发现，两自由度计算横向振幅为单自由度计算结果的1.1倍。锚索一般采用钢缆或者高分子纤维材料，其质量比小10。因此，有必要对两自由度（考虑横向和流向振动）涡激振动进行研究。假定ζ＝0.001 8，M＊＝7.8时，图7给出了锚索涡激振动幅值随约化速度U＊的变化关系。

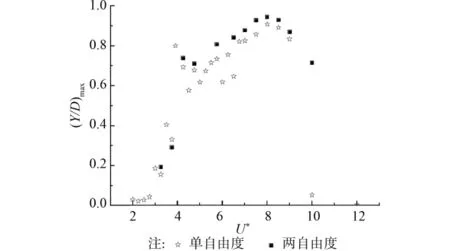
图7 不同约化速度的振幅

从图7可知，在质量比m＊＝7.8时，考虑锚索流向振动对横向振动的影响比不考虑流向振动影响得到的锚索横向振幅略有增加。除此之外，考虑流向振动影响，锚索横向振动频率锁定所对应的约化速度范围略有增加，不考虑流向振动时，锚索横向振动频率锁定的约化速度范围为［4.25，9.0］，当考虑流向振动之后，锚索横向振动频率锁定范围变为［4.25，10.0］。

限于篇幅，图8仅给出了约化速度U＊＝8.0时，锚索涡激振动位移随时间的变化关系。

图8 U＊＝8.0锚索横向位移

从位移图和频率图可知，单自由度和两自由度的锚索对应的横向振幅和频率分别为：0.908 2和1.059Hz；0.943 3和1.238Hz。由此可知，考虑流向对横向振动的影响时，锚索在涡激共振区横向振幅要大于单自由度的情况，考虑锚索流向运动对横向振幅的影响，发生涡激共振时，共振频率要小于单自由情况。

2.5 来流速度影响

为讨论流速对涡激振动的影响，假定ζ＝0.001 8，M＊＝7.8的情况下，图9给出了锚索涡激振动幅值随约化速度U＊的变化关系。

图9 不同约化速度的横向位移

从图9位移图和频率图可知，3种不同约化速度的锚索对应的横向振幅和频率分别为：0.192和0.971Hz；0.8401和1.1Hz；0.021和2.71Hz。由此可知，在涡激共振U＊＝6.5时，锚索横向振幅和频率均大于非共振情况。图9（a）、（c）分别为2种典型非共振情况，从图9（a）可以看出锚索横向振动出现拍的现象，图9（c）锚索横向振动频率远离结构固有频率，未发生涡激共振，横向位移很小。

3 结 论

1）质量比也是影响锚索涡激振动的重要因数，虽然在低质量比条件下，质量比几乎不改变涡激共振时锚索的横向振幅，但是质量比越小，锚索涡激共振对应的约化速度范围越大，锚索约容易发生涡激共振。

2）不同的阻尼对锚索横向涡激振动的幅值影响很明显，随着阻尼比的增加，锚索涡激共振时的幅值减小，涡激共振区域几乎不随锚索阻尼的变化而改变。随着阻尼比的增加，锚索涡激振动频率随着阻尼比的增加而减少，涡激振动周期增加。

3）在悬浮隧道锚索质量比较低的情况下，必须考虑锚索的顺流向振动对锚索横向振动的影响。除此之外，考虑锚索的流向振动将使锚索横向涡激共振区域变大，导致锚索更易发生涡激共振。在频率锁定区域，考虑流向运动时，锚索的横向振动幅值要大于不考虑的情况。

4）涡激共振发生时，锚索横向振幅随约化速度改变几乎不变化，位移相位发生改变。流向位移随约化速度增加而增加。

［1］Ahrens D.Submerged floating tunnels－a concept whose time has arrived ［J］.Tunneling and Underground Space Technology，1997，12（2）：317－336.

［2］董满生，葛斐，惠磊，等.水中悬浮隧道研究进展［J］.中国公路学报，2007，20（4）：101－107.Dong M S，Ge F，Hui L，et al.Research progress in submerged floating tunnels ［J］.China Journal of Highway，2007，20（4）：101－107.

［3］陈健云，孙胜男，苏志彬.水流作用下悬浮隧道锚索的动力响应［J］.工程力学，2008，25（10）：229－234.Chen J Y，Sun S N，Su Z B.Dynamic response of submerged floating－tunnel tethers subjected to current［J］.Engineering Mechanics，2008，25（10）：229－234.

［4］Zhou C Y，So R M，Lam K.Vortex－induced vibrations of elastic circular cylinders ［J］.Journal of Fluid and Structure，2004，19：449－466.

［5］Pan Z Y，Cui W C，Miao Q M.Numerical simulation of vortex－induced vibration of a circular cylinder at low mass damping using RANS code［J］.Journal of Fluids and Structure，2005，9：135－154.

［6］He C J，Duan Z D，Ou J P.Numerical simulation of self－excited and forced vibration of circular cylinders in current［J］.China Ocean Engineering，2010（1）：57－63.

［7］麦继婷，罗忠贤，关宝树.流作用下悬浮隧道张力腿的涡激动力响应［J］.西南交通大学学报，2004，39（5）：600－604.Mai J T，Luo Z X，Guan B S.Vortex－induced dynamic response of tension legs for submerged floating tunnel under current effect［J］.Journal of Southwest Jiaotong University，2004，39（5）：600－604.

［8］葛斐，董满生，惠磊，等.水中悬浮隧道锚索在波流场中的涡激动力响应［J］.工程力学，2006，23（Sup1）：217－221.Ge F，Dong M S，Hui L，et al.Vortex－induced vibration of submerged floating tunnel tethers under wave and current effects ［J］.Engineering Mechanics，2006，23（Sup1）：217－221.

［9］陈健云，王变革，孙胜男.悬浮隧道锚索的涡激动力响应分析［J］.工程力学，2007，24（10）：186－192.Chen J Y，Wang B G，Sun S N.Analysis of vortexinduced dynamic response for the anchor cable of submerged floating tunnel［J］.Engineering Mechanics，2007，24（10）：186－192..

［10］张兆顺，崔桂香，许春晓.湍流大涡数值模拟的理论与应用［M］.北京：清华大学出版社，2008.

［11］Kelkar K M，Patankar S V.Numerical prediction of vortex shedding behind a suuare cylinder［J］.International Journal Numerical Methods in Fliuds，1992，14：327.

［12］Stansby P K，Slauti A.Simulation of vortex shedding including blockage by the random－vortex and other methods［J］.International Journal Numerical Methods in Fliuds，1993，17：39－56.

［13］Feng C C.The measurement of vortex－induced effects in flow past stationary and oscillating circular and dsection cylinders［D］.University of Brithish Columbia，Vancouver，B.C，Canada，1968.

［14］Khalak A，Williamson C H K.Dynamics of a hydroelastic cylinder with very low mass and damping［J］.Journal of Fluid and Structure，1996，10：45－472.

［15］Jauvtis N，Williamson C H K.The effect of two degrees of freedom on vortex－induced vibration at low mass and damping［J］.Journal of Fluid and Structure，2004，509：23－62.

［16］黄智勇，潘志远，崔维成.两自由度低质量比圆柱体涡激振动的数值模拟［J］.船舶力学，2007，11（1）：1－9.Huang Z Y，Pan Z Y，Cui W C.Numerical simulation of VIV of a circular cylinder with two degrees of freedom and low mass－ratio ［J］.Journal of Ship Mechanics，2007，11（1）：1－9.

［17］Sarkapa T.Hydronamic damping flow－induced oscillations and biharmonic response ［J］.ASME Journal of Offshore Mechanic and Arctic Engineering，1995，117：232－238.