地下建筑人员疏散的扩展元胞自动机模拟

李蒙，李悦，林从谋

（华侨大学 土木工程学院，福建 厦门361021）

随着国家对基础设施的投资力度逐步增大，工程项目有向地下空间发展的趋势.目前，处于地面以下的项目如地下商场，地下车库，隧道，人防工程等地下工程的日益增多，虽节约了用地，扩大了城市空间但同时也带来极大的安全隐患.例如，一旦发生火灾，则损失惨重.然而，地下项目通常结构复杂，通道弯曲，人员疏散困难，易造成重大的人员伤亡和财产损失.因此，针对灾害发生时，对人员在地下建筑中的动态疏散过程进行仿真，给项目建设方、施工方、建筑设计方以及使用者提出一个合理的、及时的、安全的人员疏散方案有重要意义.元胞自动机（cellular automata，CA）模型被广泛应用于各个领域的研究.在医学领域，李璐等［1］提出基于元胞自动机的异质个体HIV／AIDS传播模型；在交通领域，刘小明等［2］提出考虑路内停车的元胞自动机交通流模型，魏丽英等［3］基于元胞自动机对自行车交通流仿真建模；在人员疏散领域，束钰等［4］基于元胞自动机对大型商贸场所火灾过程的模拟分析；在建筑领域，饶平等［5］提出复杂建筑结构人员疏散的元胞自动机模拟研究，郭玉荣等［6］提出了基于元胞自动机理论的紧急人员疏散模拟.在地下建筑方面，赵国敏［7］研究提出地铁车站人员疏散离散时间模型研究，但其研究也有自身的局限性，没有考虑到个体异质的特点，使其结果很难得到精确的结果.地下建筑发生灾害后的情况同其他建筑发生灾害的不同之处在于：其人员疏散的动态过程会不仅与地下空间结构和灾害特点相关，同时还受到个体间行为模式及个体间互动等众多因素的影响.因此，本文采用多智能体仿真技术（Agent技术）和元胞自动机结合的方法来对疏散中的人员建模，客观的模拟异质人员疏散的过程.

1 基于ECA模型的地下空间中人员疏散问题描述

在地下空间的人员疏散过程中，每个个体在每一时刻每一位置都具有不同的状态，同时，元胞自动机是一个时间和空间上离散的模型，其中的每一个元胞都代表一个复杂系统中的微观个体，具有不同的属性.因此，基于ECA模型，结合影响地下空间疏散的主要因素和邻域形式描述人员疏散的过程.

1.1 影响地下空间中人员疏散的因素

地下建筑结构不同于地上建筑，其影响疏散的主要因素有4个方面.

1）由于地下建筑的空间相对封闭，排烟、排热性差，通道相对狭窄，减缓人员的疏散速度.

2）地下建筑疏散出口有限，灾害发生后人群将大量涌向出口，一旦出口被封，后果不堪设想.

3）地下建筑不能进行自然采光，灾害时正常电源被切断，能见度降低，人员的活跃程度和疏散速度也会相应降低，使疏散的难度加大.

4）地下建筑的救援途径少，人员疏散缓慢，导致救援困难.

在地下建筑受灾后，以上几个因素影响着人员疏散的总进度，而个体是通过影响周围人的活动，又同时受周围人群的影响来间接影响整个人员的疏散进程.

1.2 ECA模型的邻域形式及距离

元胞自动机将元胞规则地排列在的空间格网上，它们各自的状态随着时间根据上一时刻该元胞的状态及该元胞的所有邻元的状态来进行更新.传统的CA模型定义了2种邻域：摩尔邻域和冯诺伊曼邻域.为了更好地描述个体间的交流互动关系，选取扩展的冯诺依曼领域进行研究.这种扩展的具有方向性的结构，可以描述个体行为在接受外界信息中所蕴含的不同偏好或某种具有倾向性的行为模式，从而对灾害发生后人员状态的变化进行描述.

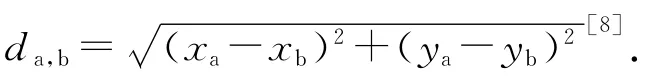
2 引入异质的个体行为的ECA模型

除ECA模型领域外，还应结合个体不同的属性，具体包括个体的活跃程度，行动速度，信息传递与信息接受能力.假定地下建筑中的个体以成年人为研究对象，并没有失去行动能力的人员.

2.1 个体的移动性

由ECA模型的邻域形式对整个地下空间不同的交通区域进行划分，建立网格.假设网格中每个单元格最多只能容纳一个个体，只能根据相应地规则移入相邻的单元格.在t时刻，根据扩展的邻域形式，个体a以概率pa从一个单元格移动到一个相邻的单元格，pa∈（pmin，pmax），（0≤pmin≤pmax≤1）［9］度量了个体的活跃程度.pa越大个体的活跃程度越高；反之，则越小 .它在仿真初始时刻指定且在仿真过程中不随时间变化.当pmin＝pmax＝0时，个体始终处于仿真开始时指定的位置，不发生移动；而当pmin＝pmax＝1时，个体在每一时刻都会移动，若周围有空的单元格就移入，若周围的单元格都已被其他个体占据，就不移动；当pmin＝pmax时，所有个体的活跃程度都相同，个体从一个单元格移动另一单元格的概率相同.由此，推算出个体移动的平均时间为1／pm，通常情况下，个体的活跃程度越高，个体的移动速度就越快，导致所在人群移动越快.

2.2 个体的信息传递与信息接受能力

个体除了具有不同的活跃程度与运动速度外，在与周围人群进行交互的过程中还具有不同的信息传递与信息接收能力，且所有人在灾害发生后都试图离开，没有人由于心理原因等情况留在危险地方.设hi表示个体i对于信息的传递能力，hi是服从（0，1）均匀分布的一个实数，该参数用来表示个体在与周围人群交流时，能将灾害危险信息传递给他人的概率.显然，hi的值越大，越有可能将使周围的个体状态发生改变；hi的值越小，则越弱.gi表示个体i对于信息的接受能力，gi是服从（0，1）均匀分布的一个实数，该参数用来表示个体在与周围人群接触时，能接受灾害危险信息的概率.每个个体对于信息的接受能力是不同的，gi越大，个体信息的接受能力越强，反之越弱.

3 仿真实验与分析

给出一个典型的试验初始值，基于不同参数，通过1 000次仿真试验，研究人员在地下建筑中的动态疏散过程.根据地下空间的结构特点，在仿真试验中主要运用扩展的冯诺依曼领域在地下空间中建立由100×100的单元格构成的网格，设定各参数的初始值为：人群数量n＝3 000，已知灾害发生个体数量占人群总数的5／1 000，总出口个数有8个，一次仿真时间为600 s.在实验过程中，人员随机分布在网格上，依据设定的规则随机移动，居中的70×70的网格中人群密度角度较大，其中，10 000个单元格中有8个是安全出口，分布在网格的四个角落及边的中点［10］，个体一旦移入此类网格，则表明个体脱离危险.易知，出口个数越多，灾害发生时的疏散速度越快.由此定义疏散效率（E）等于离开地下建筑的个体数占总人数的比值，通过个体的活跃程度，信息传递能力与信息接受能力对疏散效率的影响来描述地下建筑中的人员疏散过程.

3.1 个体的活跃程度对人员疏散效率的影响

个体的活跃程度影响人员的流动性，进而影响了整个群体的疏散效率.个体的活跃程度可以用单位时间内个体转换单元格的次数来度量.随着个体移动概率pa的增大，转换单元格的次数也将增大.在利用Repast模拟时，由于pa是离散值，为了能正确地反映随着pa变化导致的疏散效率的影响程度，拟定取值分别为p1＝0.2，p2＝0.4，p3＝0.6，p4＝0.8.当个体的信息传递能力和接受能力不变，假定分别为hi＝0.5和gi＝0.5，当pa取不同值时人员疏散效率的平均值随时间变化的仿真结果，如图1所示.由图1可知：整体的疏散效率在灾害发生前期逐渐上升，后期逐渐下降，当pa取0.2时，在一定时间内疏散效率增加缓慢，到某一时刻开始下降，波动范围小，总效率较低；当pa取0.4时，疏散效率增长较快，且达到最大值，后期下降不大；当pa取0.6时，疏散效率增长最快，但效果不如p2时的效果；当pa取0.8时，活跃程度虽然很高但疏散效率较低.由实验结果可知：个体的活跃程度在疏散过程中起了重大作用，当假定pa＝0.4时有最大的疏散效率，因此，并非个体活跃程度越大，疏散效率越高，在灾害发生时应有秩序的进行疏散.

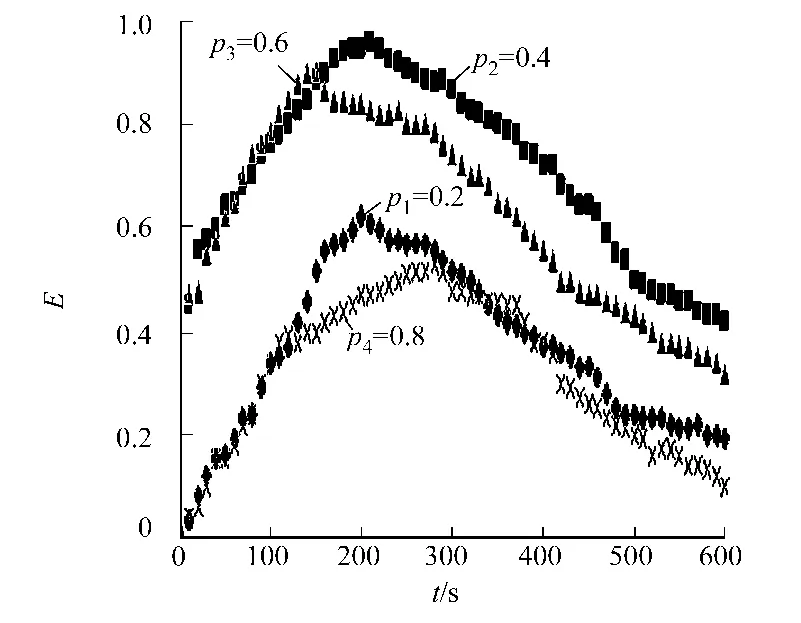
图1 个体的活跃程度对人员疏散效率的影响Fig.1 Influence of mobility on the evacuation efficiency

图2 个体的信息传递能力对人员疏散效率的影响 Fig.2 Influence of agent′s ability to spread information on the evacuation efficiency

3.2 个体的信息传递能力／信息接收能力对人员疏散效率的影响

个体的信息传递能力在疏散过程中不断影响着周围个体的信息量，正确的信息将加快疏散进度，然而错误的信息将阻碍疏散进程.当个体活跃程度pa＝0.4，信息接受能力hi，变化个体的信息传递能力hi，同样为了反映趋势，拟定hi的取值分别为h1＝0.2，h2＝0.4，h3＝0.6，h4＝0.8，如图2所示.从图2可知：疏散效率的平均值随时间变化的仿真结果，总体呈随时间增加逐渐上升，到某一时刻开始下降.在当hi等于0.2和0.8时，个体的信息传递能力较弱和较强时，人员疏散效率较低，疏散效果不明显，随时间的推移效率趋近于0；当hi等于0.4和0.6时，疏散效果好，在h3＝0.4时能达到最大的疏散效率，且效果显著.实验结果表明：并非个体传递信息的能力越强，疏散效果越好，从而灾害发生时，准确的逃生路标与信号指示显得尤为重要.

4 结束语

基于ECA模型的摩尔邻域，引入个体异质行为与疏散过程中人员的不同状态，对地下建筑中的人员疏散过程进行研究.通过个体活跃程度，信息的接受能力与传递能力对疏散效率的仿真实验，得出以下3个主要结论.

1）不论是个体活跃程度还是个体的传递与信息接收能力，随着时间的推移都会对人员疏散效率产生先增后减的影响.

2）当拟定pa取值分别为p1＝0.2，p2＝0.4，p3＝0.6，p4＝0.8时，pa＝0.4时，人员的疏散效率有最大值.这说明人员的活跃程度越大或越小，都会影响整体的疏散速度.

3）当拟定hi取值分别为h1＝0.2，h2＝0.4，h3＝0.6，h4＝0.8时，hi＝0.4时，有最大疏散效率.这说明个体接受信息的能力越强或传递信息能力越强，影响其在危险情况下的判断力.

［1］ 李璐，宣慧玉，高宝俊.基于元胞自动机的异质个体 HIV／AIDS传播模型［J］.系统管理学报，2008，17（6）：704-710.

［2］ 刘小明，王力.考虑路内停车的元胞自动机交通流模型［J］.吉林大学学报：工学报，2012，42（2）：327-333.

［3］ 魏丽英，应丽天.基于元胞自动机的自行车交通流仿真建模［J］.吉林大学学报：工学报，2011，41（1）：51-55.

［4］ 束钰，陈全.基于元胞自动机对大型商贸场所火灾过程的模拟分析［J］.天津理工大学学报，2011，27（1）：80-84.

［5］ 饶平，周晓东，朱孔金，等.复杂建筑结构人员疏散的元胞自动机模拟研究［J］.中国安全科学学报，2011，21（12）：34-39.

［6］ 郭玉荣，郭磊，肖岩.基于元胞自动机理论的紧急人员疏散模拟［J］.湖南大学学报：自然科学版，2011，38（11）：25-29.

［7］ 赵国敏，倪照鹏，张青松.地铁车站人员疏散离散时间模型研究［J］.防灾减灾工程学报，2010，30（2）：152-157.

［8］ BRAUER F，DRIESSCHE P.Models for transmission of disease with immigration of infectives［J］.Mathematical Biosciences，2001，171（2）：143-154.

［9］ HYMAN J M，LI J，STANLEY E A.The differential infectivity and staged progression models for the transmission of HIV［J］.Mathematical Biosciences，1999，155（2）：77-109.

［10］ 朱孔金，杨立中.房间出口位置及内部布局对疏散效率的影响研究［J］.物理学报，2010，59（11）：7701-7707.