基于光纤和偏振图像融合的无透镜傅里叶变换数字全息

雷莎，陈丽，何贤飞，胡义华，雷亮

（广东工业大学 物理与光电工程学院，广东 广州510006）

1965年，斯特罗克（Stroke）［1］率先提出了以球面波参考光代替平行光的无透镜傅里叶变换全息.1967年，Goodman等［2］提出了用数字方式记录和处理全息图像的数字全息技术，随后数字全息技术逐渐在诸多领域得到应用［3］.无透镜傅里叶变换数字全息光路简单，再现过程只需一次傅里叶变换，在数字全息图的记录过程中能够有效地利用电荷耦合元件（CCD）的带宽，提高再现像的分辨率 .因此，无透镜傅里叶变换数字全息术已经受到越来越多研究人员的关注［4］.与菲涅耳数字全息［5］不同的是，无透镜傅里叶变换数字全息的参考光采用球面波而非平行光，全息图所记录的是物光的空间频谱而非物光本身［6-7］.其无需知道记录距离就可以得到再现像的强度分布，不仅能大大节约运算时间，而且能够得到更为准确的再现像.图像融合是将两幅或者多幅不同的图像用一定的融合方法［8］组合成为一幅新的图像，融合后的图像提供了比原图像更好的性能［9］.偏振图像反映了物体和入射光的偏振特性，国内外已经将偏振图像融合技术应用到军事和民用的诸多领域［10-11］.Muller等［12］利用多幅全息图叠加取平均的方法来提高再现像的信噪比，Freddy等［13］通过一百张相互独立的数字全息图像的叠加，再取得平均值，有效地消除了散斑噪声.本文将偏振图像融合技术应用到无透镜傅里叶变换数字全息中，不仅消除了散斑噪声，而且提高了再现像的分辨率.

1 无透镜傅里叶变换数字全息原理

无透镜傅里叶变换数字全息记录光路，如图1所示.设物光为O，参考点光源为R，物体与参考光位于同一平面x0y0上，X轴在参考点光源的坐标为（xr，0），CCD光敏面位于平面xy上，并且CCD的光敏面与Z轴重合，两平面之间的距离为d0.

CCD所记录的是物体的无透镜傅里叶变换全息图的空间频谱，其再现像［14］可表示为

式（1）中：C为复常数；FF表示受到1／λd0调制的二维傅里叶变换.

记录过程中，为抵消菲涅耳衍射积分中的二次位相因子，可以采用球面参考光波r（x，y）式对其进行抵消，即

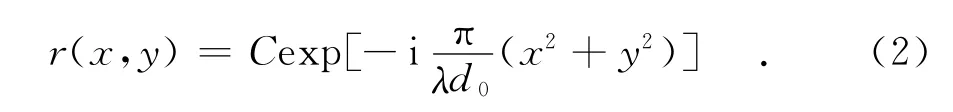
因此，再现像的光强可以简单地表示为

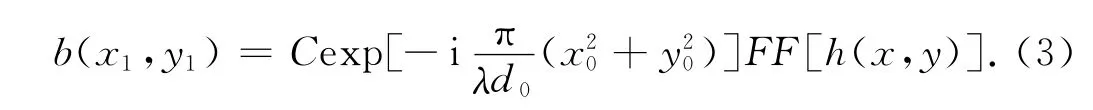
从式（3）可以看出，仅使用一次快速傅里叶变换算法，就能够再现出无透镜傅里叶变换全息图的再现像.

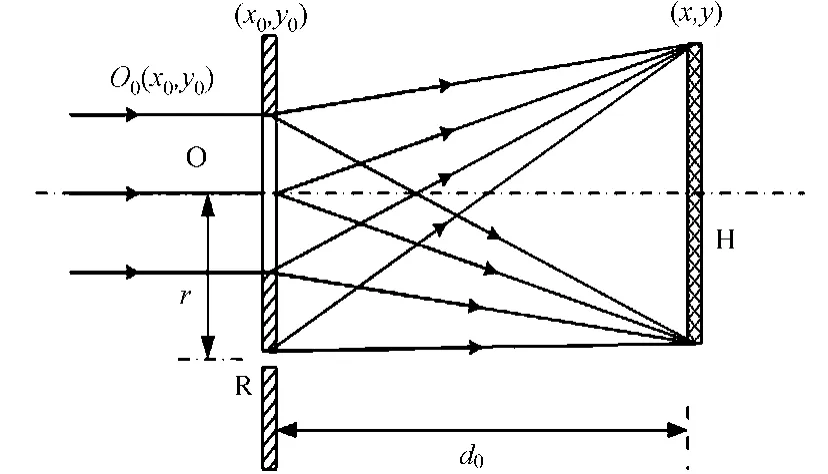
图1 无透镜傅里叶变换数字全息记录光路图Fig.1 Light path for recording holograms of lensless Fourier transform digital holography

2 实验结果与分析

基于光纤的无透镜傅里叶变换数字全息实验光路图，如图2所示.实验中，选用的记录物体是一个白色的骰子（12 mm×12 mm×12 mm），半导体激光器（波长为532 nm）发出的光经分光镜BS分成两束.其中一束光经过扩束镜EP1和准直透镜L1组成的扩束准直系统形成平行光波，平行光波经聚焦透镜L2聚焦后射入光纤端面，从光纤另一端面射出的球面波作为参考光直接射向CCD光敏面（像素数为1 200×1 600，像素尺寸为4.4μm×4.4μm）；另一束经过全反镜M改变方向后，被扩束镜EP2扩束后直接照射物体表面，经物体反射后投射到CCD光敏面形成物光.两束光在CCD光敏面上发生干涉形成数字全息图.

光路中的CL是平面凹透镜，其作用是为物体提供预成像，扩大全息图的记录与再现范围.一段具有高数值孔径的单模光纤的出射端面作为参考光的点光源，与物体共面.

根据傅里叶变换的性质，无透镜傅里叶变换全息能够再现两个中心对称的再现像，可避免菲涅耳全息中对一个再现像聚焦，另一个再现像会产生离焦的问题.没有使用光纤的菲涅尔数字全息图的再现像，如图3所示.由图2所示的光路图得到的无透镜傅里叶变换数字全息再现像，如图4所示.

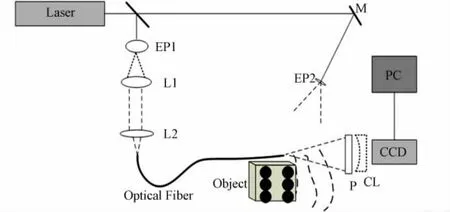
图2 基于光纤的无透镜傅里叶变换数字全息光路图Fig.2 Experimental setup of lensless Fourier transform digital holography based on optical fiber

图3 菲涅尔数字全息图Fig.3 hologram of Fresnel digital holography

图4 无透镜傅里叶变换全息图Fig.4 Hologram of lensless Fourier transform digital holography

在CCD前放置一偏振片记录物光的偏振信息，改变旋转偏振片的角度（θ），得到的无透镜傅里叶变换数字全息偏振图如图5所示 .将图5的6幅图合成，可以得到偏振合成的再现像，如图6所示.最后，对再现像进行中值滤波［15］处理后，即得到如图7所示的图像.

相比于普通的数字全息，使用了光纤的无透镜傅里叶变换数字全息具有如下4个特点：1）光路装置简单、紧凑、灵活且便于使用；2）光路中省去了透镜，可以避免由透镜带来的球面像差等非线性影响；3）无透镜傅里叶变换全息图的数值再现算法相对简单，只需进行一次傅里叶变换即可；4）由于采用球面参考光波，得到全息图的横向分辨率较高，并能充分利用CCD的空间带宽等.

图5 不同偏振器角度的无透镜傅里叶变换数字全息偏振图Fig.5 Polarization diagram of lensless Fourier transform digital holography with different polarization angle

图6 偏振合成的再现图Fig.6 Reconstruction after polarization image fusion

图7 中值滤波处理后的再现图 Fig.7 Reconstruction after median filtering

将高数值孔径的单模光纤引入无透镜傅里叶变换数字全息，有如下4点的优点：1）光纤具有传送和扩束的功能，在布置光路时使用的元件较少；2）能避免球面像差；3）对环境要求不高，抗干扰能力强；4）单模光纤纤芯直径大约为4～10μm，其传光特性较好，输出光可以看作一个理想的点光源，无需针孔滤波器，就可以用作参考光源.

偏振片的加入是本系统与其他系统的主要区别，偏振片对入射光有遮蔽和透过的功能.从图5～10可以看出：加入偏振片后，再现像的光强变弱了.比较实验所得的再现像图4与图6，可以证实偏振图像融合的方法在无透镜傅里叶变换数字全息实验中，不仅能记录物光的振幅、相位、偏振信息，而且能减少实验环境所产生的噪声和误差，减小图像的噪声含量，提高再现像的分辨率.由于激光散斑和其他杂散光等噪声的影响较大，实验得到的再现图的光强不均匀，局部有些不清晰.通过中值滤波后，所得到的再现像（图7）相对光线柔和，图像较为清晰.

3 结论

采用基于光纤和偏振图像融合的无透镜傅里叶变换数字全息，不仅实验装置简单、灵活，记录了物体的相位、振幅和偏振信息，而且能得到清晰的再现像.高数值孔径单模光纤的引用，方便消除了球面相差、噪声等的影响，提高了再现像的质量.

偏振图像融合技术减少了图像的噪声含量，中值滤波器［14］减少了实验噪声，提高了再现像的分辨率.由于记录结果仍然受记录条件等其他原因的影响，如何消除这些因素将是进一步需要研究的问题.

［1］ STROKE G W.Stroke.Lensless fourier transform method for optical holography［J］.Applied Physics Letters，1965，6（10）：201-203.

［2］ GOODMAN J W，LAWRENCE R W.Digital image formulation from electronically detected hologram［J］.Appl Phys Letter，1967，11（3）：77-99

［3］ 崔华坤，王大勇.无透镜傅里叶变换数字全息术中非共面误差的自动补偿算法［J］.物理学报.2011（4）：044201.

［4］ Li Chen，Xiao Ma.Color holographic image by using digital lensless Fourier transform holography with optical fiber.Optical Engineering［J］.2012，51（4）：045802.

［5］ 张燕，刘轩.菲涅耳全息图的数字再现方法比较［J］.山东师范大学学报：自然科学版，2007，22（3）：47.

［6］ ZHAO Jian-lin，JIANG Hong-zhen，DI Jiang-lei.Recording and reconstruction of a color holographic image by using digital lensless Fourier transform holography［J］.Optics Express，2008，16（4）：2514-2519.

［7］ 田爱玲，薛小卫.无透镜傅里叶变换数字全息记录与再现［J］.西安工业大学学报，2009，29（1）：4-7.

［8］ 张德祥，张晶晶.基于 Directionlets变换的偏振图像融合［J］.电子与信息学报，2011，12（33）：2795-2800.

［9］ 赵永强，潘泉.基于偏振成像技术和图像融合理论杂乱背景压缩［J］.电子学报，2005，3（33）：433-435.

［10］ 陈伟力，王霞.基于小波包变换的中波红外偏振图像融合研究［J］.北京理工大学学报，2011，31（5）：578-610.

［11］ 王新，王学勤.基于偏振成像和图像融合的目标识别技术［J］.激光与红外，2007，37（7）：676-678.

［12］ MULLER J，KEBBEL V，JUPTNER W.Digital holography as a tool for testing high-aperture micro-optics［J］.Optics and Lasers in Engineering，2005，43（7）：739-751.

［13］ MONROY F A，GARCIA-SUCERQUIA J.Increment of lateral resolution in digital holography by speckle noise removal［J］.Optik ，2010，121（22）：2049-2052.

［14］ 袁操今，钟丽云，朱越.无透镜傅里叶变换数字全息术的特点分析和讨论［J］.激光杂志，2004，25（5）：59-61.

［15］ 高浩军，杜宇人.中值滤波在图像处理中的应用［J］.电子工程师，2004，30（8）：35-36.