ZnO薄膜/金刚石在不同激励条件下声表面波特性的计算与分析*

钱莉荣 杨保和

1)(天津大学精密仪器与光电子工程学院，天津 300072)

2)(天津理工大学电子信息工程学院，天津市薄膜电子与通信器件重点实验室，天津 300384)

(2013年1月8日收到;2013年2月22日收到修改稿)

1 引言

随着高速、宽带、无线移动通信系统的迅速发展和应用普及，对高频、宽带、大功率、低损耗声表面波器件的需求也越来越大.金刚石具有目前已知材料中最高的声速和最大的热导率，非常适合做高频、大功率声表面波器件的基片[1-3]，但其没有压电性，所以需要在其表面添加压电薄膜才能激励声表面波，这便构成了压电薄膜/金刚石复合基片.在常见的压电薄膜中，具有高度c轴择优取向的多晶ZnO是目前应用最为广泛的一种薄膜材料[4-6]，它不仅具有较高的机电耦合系数，而且制备工艺简单、成熟.另外，最近的研究表明[7]，通过在 ZnO 薄膜中掺杂少量的 Cu，Co，V，Cr，Fe，Mn等过渡金属，可以显著地提高其压电特性，这对于低损、宽带声表面波器件的应用具有十分重要的意义[8-10].

与传统单晶基片(如石英、铌酸锂、钽酸锂等)不同，ZnO薄膜/金刚石这种复合基片中的声表面波具有频散特性，所以由其制作的器件性能也会随ZnO膜厚和声表面波波长(或频率)的变化而不同[11-13].而且这种复合基片的声表面波可以有四种激励方式[14,15]，即叉指电极(IDT)/ZnO/金刚石 (I-F结构)、IDT/ZnO/短路金属/金刚石 (IM 结构)、ZnO/IDT/金刚石 (F-I结构)和短路金属/ZnO/IDT/金刚石(M-I结构)，在不同的激励条件下，其声表面波特性也会不同.因此，准确地计算ZnO薄膜/金刚石在四种激励条件的声表面波特性是应用这种复合基片设计制作高性能声表面波器件的基础.

在ZnO薄膜/金刚石声表面波特性的计算方法中，Campbell的分波法[14,16]和Adler的传递矩阵法[15,17]是最为常见的两种方法.与传统的分波法相比，传递矩阵法具有数值计算复杂度与介质层数无关、易于编程等优点[17]，所以近些年来在多层介质声波特性的计算中应用得更为广泛.但当介质层厚度与声波波长之比较大时，传递矩阵法会出现数值计算不稳定性问题[18-21].为了解决该问题，表面阻抗矩阵[18]、散射矩阵[19]、反射矩阵[20]和刚度矩阵[21]等方法在传递矩阵法的基础上被相继提了出来，利用这些方法能够计算任意层数、任意层厚压电多层介质的有效介电常数或格林函数[19-22]，而有效介电常数或格林函数又是研究基片声表面波特性及其器件建模的重要手段和工具[12,22-27].

目前大多数文献仅给出了I-F结构下ZnO薄膜/金刚石的有效介电常数或格林函数的计算方法[12,20,21,25]，其他三种激励方式的却鲜见介绍[28]，而且在计算过程中都采用的是ZnO和金刚石的单晶材料常数[14,28]，但在实际基片材料中[3]，金刚石为多晶薄膜，在其上也无法外延出单晶ZnO，所以研究c轴择优取向多晶ZnO薄膜/多晶金刚石复合基片的声表面波特性具有现实意义，对此国内外未见有报道.

本文首先以刚度矩阵法为基础，通过定义表面刚度矩阵，推导出ZnO薄膜/金刚石在四种不同激励条件下的有效介电常数计算公式.然后以有效介电常数为工具，计算单晶ZnO薄膜/多晶金刚石和多晶ZnO薄膜/多晶金刚石在四种不同激励条件下声表面波的相速度和机电耦合系数频散特性，并通过与相关文献中实验数据的比较，讨论激励条件的差异和ZnO薄膜材料参数的不同对声表面波特性的影响.最后根据设计和制作多层结构声表面波器件的要求，对ZnO/金刚石基片中ZnO膜厚和金刚石膜厚如何选择的问题进行探讨和分析.

2 理论推导

在各向异性压电介质中传播的声表面波，必须同时满足动力学方程和麦克斯韦方程.在准静态近似下，当介质中自由电荷近似为零时，利用爱因斯坦附标求和惯例，可以将声表面波场的控制方程简洁地表示为如下张量形式：

图1 ZnO薄膜/金刚石多层声表面波介质坐标系

对于图1所示坐标系，为了求得方程(1)—(4)的解，假设沿x1方向传播的平面谐波，其质点位移ui和电势φ具有如下解的形式：

(10)式表明压电层状介质中声波的解，可以表示为8个声平面谐波的线性组合，其中4个分波沿正x3方向传播或衰减，4个分波沿负x3方向传播或衰减.由于(10)式解中混合着指数衰减项和指数增长项，从而会为数值计算带来不稳定性[12,18-21]，为了提高解的稳定性，利用Wang和Rokhlin提出的刚度矩阵法[21]对(10)式进行分解重构.

2.1 刚度矩阵

对于任意层数压电多层介质的计算，可以通过递归调用(17)或(18)式得到其总表面刚度矩阵.

2.2 有效介电常数

对于ZnO薄膜/金刚石多层介质，声表面波的激励可以有四种方式[14,15]，如图2所示，其中叉指换能器(IDT)用于实现声电转换，而金属薄膜用于使压电薄膜表面短路，一般而言叉指电极和短路金属薄膜很薄，故其质量负载的影响可以忽略.在不同的激励方式下，介质的边界条件不同，所以其声表面波特性也有所差异.表面有效介电常数εs是计算压电介质表面声表面波特性的有效方法，它通常定义为[23]

图2 ZnO薄膜/金刚石多层介质中四种声表面波激励方式 (a)I-F结构;(b)I-M结构;(c)F-I结构;(d)M-I结构

为了便于定义有效介电常数，将(16)式和(19)式中的表面刚度矩阵Ks展开为如下形式：

2.2.1 表面源结构：I-F和I-M

2.2.2 界面源结构：F-I和M-I

2.3 声表面波特性的计算

声表面波波速和机电耦合系数是设计声表面波器件必须要掌握的基本声学参数，这两个参数都可以利用有效介电常数εs计算得到.

3 计算结果与讨论

根据上节推导的有效介电常数εs计算公式，编制程序计算c轴择优取向ZnO薄膜/金刚石复合基片在四种激励条件下的声表面波特性.计算所用材料参数见表1所示，其中金刚石采用的是多晶薄膜参数，而ZnO薄膜使用的是单晶和多晶两种材料参数，这是因为在实际基片材料中[3]，金刚石通常是硅基多晶薄膜，而ZnO薄膜的材料参数通常与制备方法和条件有关.为便于描述和行文，以后用s-ZnO表示单晶ZnO(002)薄膜，p-ZnO表示多晶ZnO(002)薄膜，Dia表示多晶金刚石膜.

图3是s-ZnO/Dia在F-I结构下k1hZnO=2时的相对有效介电常数 εs/ε∞，其中 k1=2π/λ 为声表面波传播方向波数.在所考察的3—9 km/s相速度范围内，图中有效介电常数εs的虚部始终为零，这表明声波能量始终集中于介质表面附近，没有泄漏到金刚石基底内部，所以εs实部在相速度为4405 m/s，5819 m/s和8179 m/s附近的三对零极点，分别对应于三种声表面波模式的自由表面波速和金属化表面波速.若以k1hZnO作为自变量，以εs的零点作为函数，可以计算得到ZnO/Dia的自由表面波相速度频散曲线.

图4是s-ZnO/Dia(粗实线)和p-ZnO/Dia(细虚线)分别在(a)I-F和(b)F-I结构下前三种声表面波模式的相速度，图中散点为文献[1]中的实验数据，从计算结果与实验数据的比较可以看到，两者符合得较好，而p-ZnO/Dia中的相速度要比s-ZnO/Dia中的低一些.值得注意的是，对于基模(M0)声表面波，随着ZnO膜厚与波长之比hZnO/λ由0增大到∞，其波速由金刚石本身的瑞利波波速(∼10936 m/s)减小到ZnO的瑞利波波速(∼2531 m/s)，所以M0实际上是传统意义上的Rayleigh波;而高次模式则在金刚石的剪切体声波波速(∼12323 m/s)处表现出截止特性，其中一次模(M1)称为Sezawa波.需要特别指出的是，在 k1hZnO=1.22(s-ZnO/Dia)或 k1hZnO=1.48(p-ZnO/Dia)附近时，Rayleigh波和Sezawa波的相速度非常接近，而并非文献[1]中所认为的相交[15].

表1 计算所用材料参数

图3 s-ZnO/Dia在F-I结构下k1hZnO=2时的相对有效介电常数 εs/ε∞

图5是利用有效介电常数计算的s-ZnO/Dia和p-ZnO/Dia在四种不同激励条件下前三种声表面波模式的机电耦合系数(K2)频散曲线，与图4中对相速度的影响相比，激励条件的不同对机电耦合系数的影响要显著得多.而且K2对ZnO材料参数的变化也比较敏感，虽然多晶ZnO与单晶ZnO的K2总体变化趋势相似，但其数值通常比单晶ZnO的要小一些，特别是对于Sezawa波表现得更明显.而对于Rayleigh波，在F-I和M-I结构下当ZnO膜厚hZnO/λ较小时，其多晶ZnO的K2却比单晶ZnO的要大.通过与文献[1]实验数据的比较可以看到，在图5(a)的I-F结构中，实验数据与s-ZnO/Dia的计算结果符合得好一些;而在图5(c)的F-I结构中，实验结果却与p-ZnO/Dia的计算结果符合得更好.

图4 ZnO/Dia在(a)I-F和(b)F-I结构下前三种声表面波模式的相速度(s-ZnO：单晶ZnO;p-ZnO：多晶ZnO;Dia：多晶金刚石)

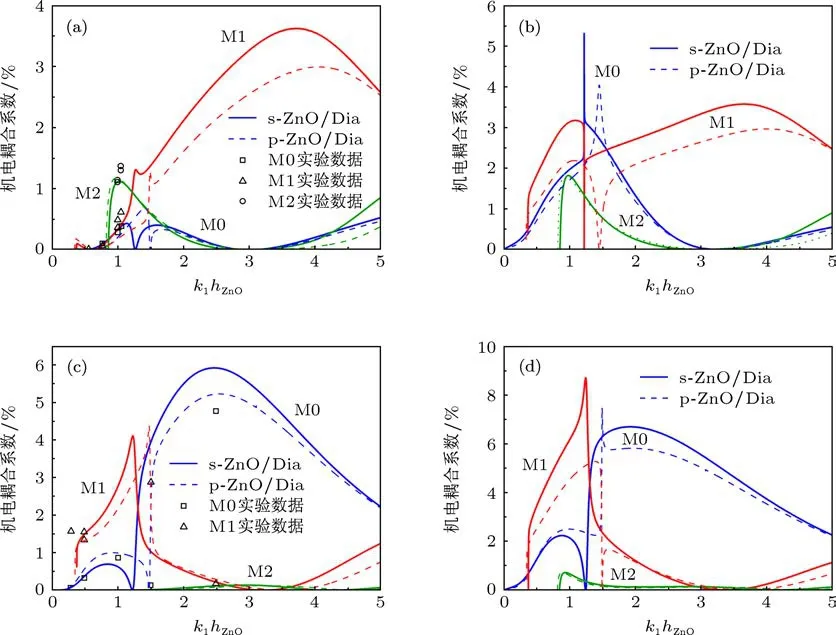
图5 ZnO/Dia在四种激励条件下前三种声表面波模式的机电耦合系数 (a)I-F结构;(b)I-M结构;(c)F-I结构;(d)M-I结构

从图4和图5的比较中我们还注意到，在k1hZnO=1.22(s-ZnO/Dia)或k1hZnO=1.48(p-ZnO/Dia)附近，即Rayleigh波和Sezawa波相速度十分接近的区域，其对应的K2也变化得异常快(特别是在I-M结构下).为了探究其中的原因，我们以I-M结构下的s-ZnO/Dia为例，考察了其Rayleigh波和Sezawa波在该区域附近位移场的变化情况，如图6所示，图中 |u1|，|u2|和|u3|分别为声表面波位移矢量纵向(x1方向)分量、水平剪切(x2方向)分量和垂直剪切(x3方向)分量的相对幅度，由于|u2|始终为零，而u1和u3相位相差π/2，所以声表面波位移矢量在x1-x3平面内形成椭圆偏振.注意到随着k1hZnO由1.21增大到1.24，其Rayleigh波位移矢量由纵向分量占主导的椭圆偏振态变化为由垂直剪切分量占主导的椭圆偏振态，而Sezawa波位移矢量的变化情况则与之相反，特别是在k1hZnO=1.2263附近时，两种模式位移矢量的偏振态出现互换，这可能是导致两者相速度十分接近及K2异常变化的原因.

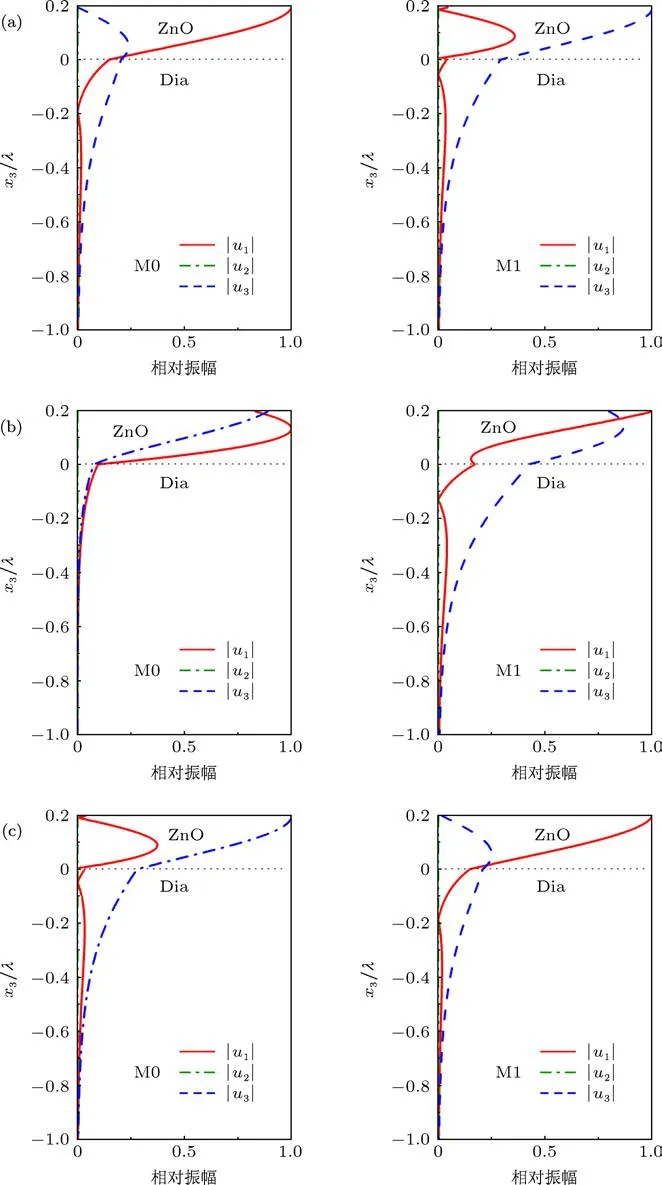
图6 s-ZnO/Dia在I-M结构下Rayleigh波(M0)与Sezawa波(M1)在不同k1hZnO时位移场的变化 (a)k1hZnO=1.21;(b)k1hZnO=1.2263;(c)k1hZnO=1.24

在应用ZnO/Dia基片设计声表面波器件时，ZnO薄膜厚度hZnO的选择至关重要，这不仅要考虑获得更大的机电耦合系数K2和更高的声速Vp，还应尽量减小频散对器件特性的影响[11,12]，从而降低器件制作过程中对工艺精度的要求，对此我们需要从图4和图5中综合考虑上述因素.

首先看Rayleigh波(M0)，从图5中注意到，在I-F，F-I和M-I结构中，机电耦合系数K2存在两个峰值，在前一个峰值处，其对应于图4中的相速度较高，而且频散也不大，所以满足设计器件的要求.而在K2的后一峰值处，虽然K2可能很高(如在M-I中为6.7%)，但其对应的Vp却不大(如M-I中为4493 m/s)，这就失去了较传统单晶基片所具有的高声速优势.在I-M结构中，由于K2在其峰值附近变化太快，且对应的Vp频散很大，所以在此很难制作出稳定可靠的器件.但可以选择靠近K2峰值的左侧进行设计，因为此处K2和Vp都较高，而且Vp的频散也不大.

对于 Sezawa波 (M1)，从图 4中可以看到，在 k1hZnO＜ 1.0(或 hZnO＜ 0.16λ)的高声速(＞7000 m/s)区域，其对应于图5中I-M，F-I和M-I结构中的K2也很大，这虽然有利于高频器件的应用，但Vp在此区域内的高频散特性，也使器件制作工艺的难度增大.在k1hZnO＞1.0(或hZnO＞0.16λ)的低声速区域，虽然相速度不高，但其频散也很小，甚至优于Rayleigh波，而且对应的K2很高，若在K2峰值附近设计谐波器件，也同样可以制作出高频器件[33,34].

对于二次模(M2)，从图5中可以明显看到，其在F-I结构中的K2很小(＜0.15%)，所以很难应用于实用器件.而在I-F，I-M和M-I结构中，其在k1hZnO=1.0(或 hZnO=0.16λ)附近的 K2较高，且对应于图4中的相速度大于10000 m/s，Vp的频散也适中，若能控制好膜厚hZnO的精度，有可能在此制作出较好的高频器件.

表2和表3总结了s-ZnO/Dia和p-ZnO/Dia在四种激励方式下前三种模式中较为适合制作器件的一些典型ZnO膜厚值hZnO、及其相应的相速度Vp、机电耦合系数K2和Vp的频散大小，其中Vp的频散值未见有文献给出过明确定义[11,12]，本文则以Vp在中心频率 f附近随膜厚hZnO的变化值d(Vp)/d(fhZnO)来表示，其物理意义可以理解为：当中心频率 f=1 GHz时，实际制备的ZnO膜厚hZnO比理论设计值相差1 nm时Vp变化的大小.由于IDT周期λ的单位通常为µm，所以当相速度Vp变化1 m/s时，实际器件的中心频率将与理论设计值 f相差约1/λMHz.实际上在ZnO薄膜/金刚石器件的制作过程中，ZnO膜厚是最难掌控的参数，一般都会与设计值存在一定的误差，所以Vp的频散值对于多层结构器件的设计和制作具有重要的参考价值.

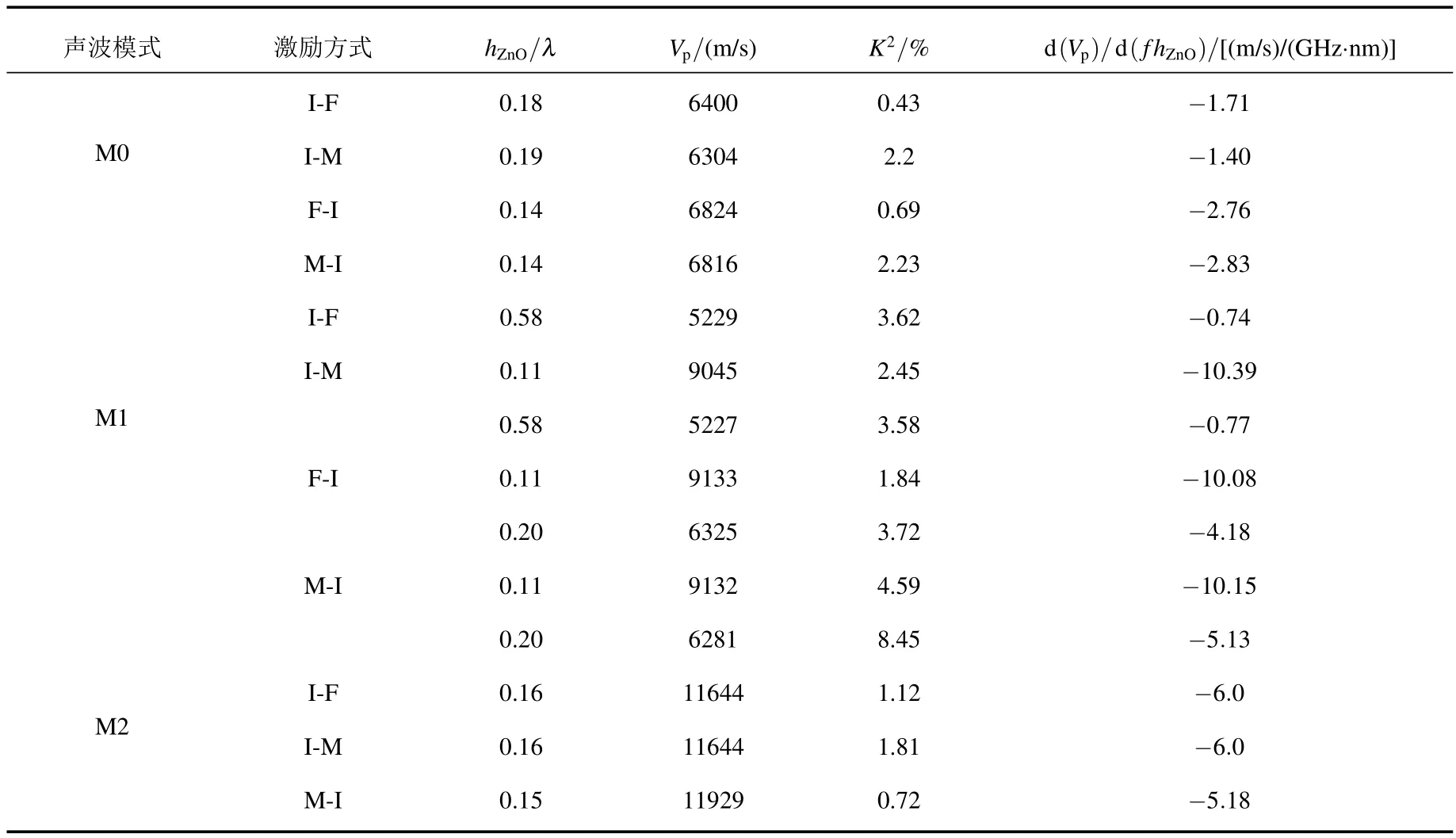
表2 s-ZnO/Dia在不同激励方式下前三种模式声表面波特性典型参数值

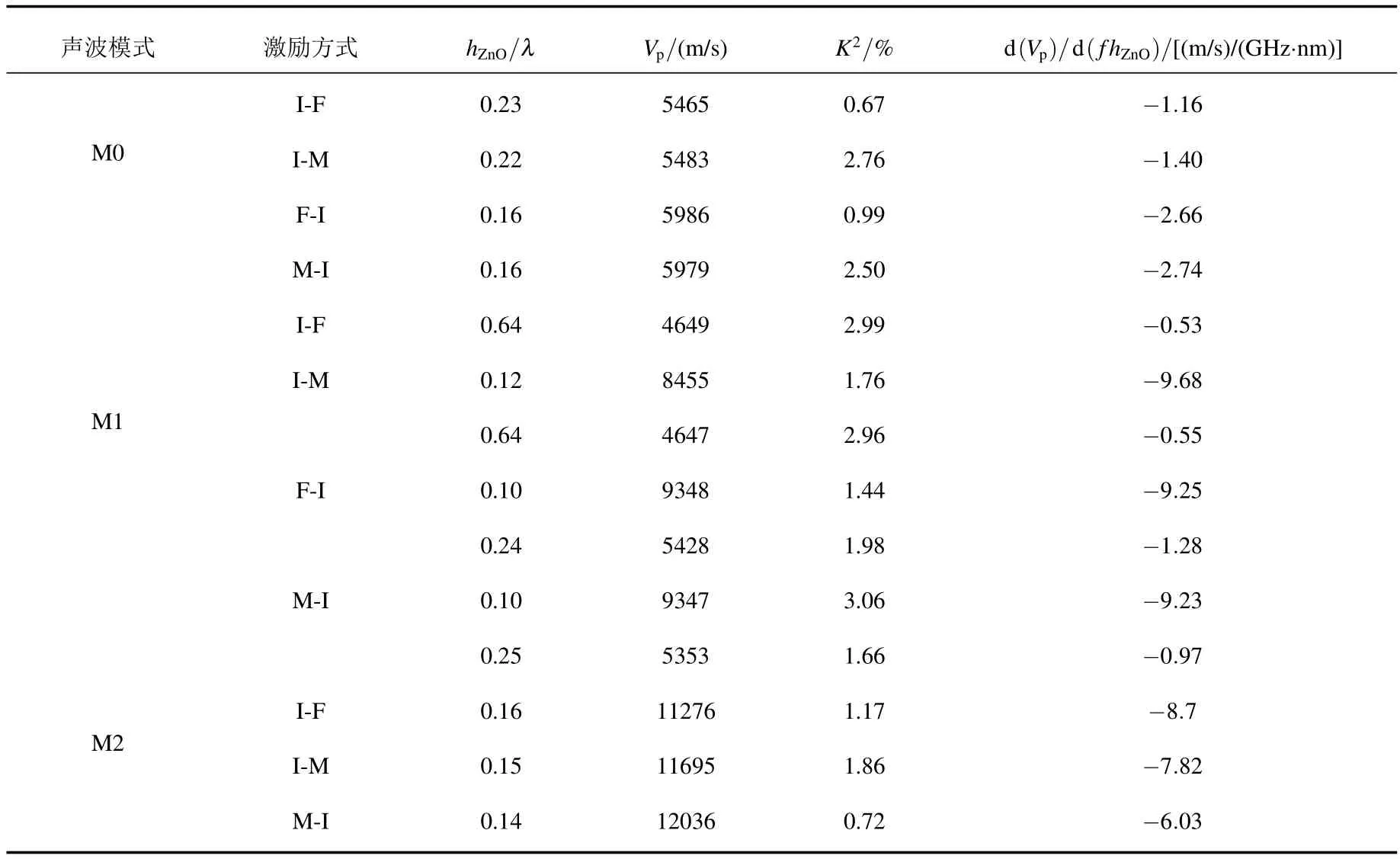
表3 p-ZnO/Dia在不同激励方式下前三种模式声表面波特性典型参数值

最后要说明的是，在常见的Si基金刚石膜晶片中，金刚石膜厚hDia的选择也很重要.对此有些文献认为[1,14]，当 k1hDia≥4(或 hDia/λ≥0.64)时，ZnO/Dia/Si中的声表面波能量将主要集中于ZnO/Dia层中而很难到达Si衬底.为了验证这一结论，我们计算了F-I结构下s-ZnO/Dia/Si中Rayleigh波在不同金刚石膜厚hDia时的传播损耗，如图7所示，当金刚石膜厚hDia有限且k1hZnO＜1.44时，Rayleigh波波速将超过硅衬底的慢剪切体波波速(∼5645 m/s)，所以其部分能量会通过与体声波的耦合而泄漏到Si衬底内部，从而引起能量损耗，实际上此时的声表面波已成为漏表面波.对于漏表面波，当其传播损耗小于10-3dB/λ时[35]，其传播损耗对器件的影响就可以忽略.若以此为标准对图7进行考察后会发现，当hZnO/λ较小时，ZnO/Dia/Si中的金刚石膜厚hDia至少应满足hDia≥2λ才能忽略Si衬底的影响，此时ZnO/Dia/Si中的声表面波特性与ZnO/Dia中的基本相同.例如文献[1]中的实验数据虽然是在ZnO/Dia/Si基片上所测，但由于其金刚石膜厚hDia=20µm[36]，测试器件的IDT周期λ=6或8µm[1]，显然满足hDia＞2λ，所以其实验数据与本文所计算的ZnO/Dia声表面波特性结果符合得很好.

图7 s-ZnO/Dia/Si在F-I结构下Rayleigh波在不同金刚石膜厚hDia时的传播损耗

4 结论

本文以刚度矩阵法为基础，推导了ZnO薄膜/金刚石在I-F，I-M，F-I和M-I四种激励条件下的有效介电常数计算公式，并以此为工具计算了多晶ZnO(002)薄膜/多晶金刚石和单晶ZnO(002)薄膜/多晶金刚石四种激励条件下声表面波模式的相速度和机电耦合系数频散曲线，通过与相关文献中实验数据的比较，验证了本文计算方法的有效性.此外，从计算结果的讨论和分析中发现：1)相比于声表面波的相速度，其机电耦合系数对激励条件的不同和ZnO材料参数的差异都要敏感得多，而且当ZnO膜厚较小时，多晶ZnO中的K2有可能比单晶ZnO中的大;2)在Rayleigh波和Sezawa波相速度十分接近的特殊区域，其机电耦合系数也出现了快速变化的现象，这可能与该区域附近两种模式位移偏振态的互换有关.最后本文列出了ZnO薄膜/金刚石基片在四种激励方式下前三种声表面波模式的一些典型声学参数，如ZnO膜厚、相速度、机电耦合系数及相速度频散值等，这些参数对于金刚石膜厚hDia≥2λ(λ为叉指电极周期)的ZnO/金刚石/Si晶片仍然适用，所以对于高频金刚石声表面器件的设计和制作具有重要的参考价值.

[1]Nakahata H，HigakiK，FujiiS，HachigoA，KitabayashiH，Tanabe K，SekiY，Shikata S 1995 Proc.IEEE Ultrason.Symp.1 361

[2]HigakiK，Nakahata H，KitabayashiH，FujiiS，Tanabe K，SekiY，Shikata S 1997 IEEE Trans.Ultrason.Ferroelect.Freq.Contr.44 1395

[3]FujiiS，SekiY，Yoshida K，Nakahata H，HigakiK，KitabayashiH，Shikata S 1997 Proc.IEEE Ultrason.Symp.1 183

[4]Guang Y，Santos P V 2007 Acta Phys.Sin.56 3515(in Chinese)[杨光，Santos P V 2007物理学报56 3515]

[6]Fu Y，Garcia-GancedoL，Pang H，PorroS，Gu Y，LuoJ，Zu X，PlacidoF，Wilson J，Flewitt A 2012 Biomicrofluidics 6 024105

[7]Pan F，LuoJ T，Yang Y C，Wang X B，Zeng F 2012 Sci.China Tech.Sci.55 421

[8]LuoJ，Zeng F，Pan F，LiH，Niu J，Jia R，Liu M 2010 Appl.Surf.Sci.256 3081

[9]LuoJ，Fan P，Pan F，Zeng F，Zhang D，Zheng Z，Liang G，CaiX 2012 Phys.Status SolidiRRL 6 381

[10]LuoJ，Pan F，Fan P，Zeng F，Zhang D，Zheng Z，Liang G 2012 Appl.Phys.Lett.101 172909

[11]HachigoA，Malocha D C 1998 IEEE Trans.Ultrason.,Ferroelect.Freq.Contr.45 660

[12]Wu T T，Chen Y Y 2002 IEEE Trans.Ultrason.,Ferroelect.Freq.Contr.49 142

[13]Wu T T，Chen Y Y，Chou T T 2002 Proc.IEEE Ultrason.Symp.1 271

[14]Nakahata H，HachigoA，HigakiK，FujiiS，Shikata S，FujimoriN 1995 IEEE Trans.Ultrason.Ferroelect.Freq.Contr.42 362

[15]Adler E L，Solie L 1995 Proc.IEEE Ultrason.Symp.1 341

[16]CampbellJ J，Jones W R 1968 IEEE Sonics and Ultrason.15 209

[17]Adler E L 1990 IEEE Trans.Ultrason.,Ferroelect.Freq.Contr.37 485

[18]Levent Degertekin F，Honein B，Khuri-Yakub B 1996 Proc.IEEE Ultrason.Symp.1 559

[19]Pastureaud T，Laude V，Ballandras S 2002 Appl.Phys.Lett.80 2544

[20]Tan E L 2002 IEEE Trans.Ultrason.,Ferroelect.Freq.Contr.49 929

[21]Wang L，Rokhlin S L 2004 IEEE Trans.Ultrason.,Ferroelect.Freq.Contr.51 453

[22]Zhang V Y，Lefebvre J E，BruneelC，Gryba T 2001 IEEE Trans.Ultrason.Ferroelect.Freq.Contr.48 1449

[23]Milsom R F，Reilly N H C，Redwood M 1977 IEEE Sonics and Ultrason.24 147

[24]DonghaiQ，Wen L，Smith P M 1999 IEEE Trans.Ultrason.,Ferroelect.Freq.Contr.46 1242

[25]Smith P M 2001 IEEE Trans.Ultrason.,Ferroelect.Freq.Contr.48 171

[26]Peach R C 2006 IEEE Ultrason.Symp.Vancouver，BC，Oct.2—6，2006 p371

[27]Chen Y Y，Hsu J C，Wu T T 2004 J.Chin.Inst.Eng.27 823

[28]HashimotoK 2000 Surface acoustic wave devices in telecommunications：modelling and simulation(Berlin：Springer)p165

[29]BenettiM，Cannata D，DiPictrantonioF，Verona E 2005 IEEE Trans.Ultrason.Ferroelect.Freq.Contr.52 1806

[30]CarlottiG，SocinoG，PetriA，Verona E 1987 IEEE Ultrason.Symp.Denver，Colorado，USA，Oct.14—16，1987 p295

[31]Jaffe H，Berlincourt D A 1965 Proc.IEEE 53 1372

[32]HachigoA，Nakahata H，Itakura K，FujiiS，Shikata S 1999 Proc.IEEE Ultrason.Symp.1 325

[33]Nakahata H，HachigoA，Itakura K，Shikata S 2000 IEEE Ultrason.Symp.1 349

[34]Morgan D 2007 Surface acoustic wave filters(2nd Edn.)(Oxford：Elsevier)p343

[35]Shikata S，Nakahata H，HigakiK，HachigoA，FujimoriN，YamamotoY，SakairiN，TakahashiY 1993 Proc.IEEE Ultrason.Symp.1 277