基于EZW的图像压缩和树形加密同步算法*
邓海涛 邓家先 邓小梅
(海南大学信息科学技术学院,海口 570228)
(2012年12月6日收到;2013年1月8日收到修改稿)
1 引言
对各类电子信息进行加密,以保证在其处理、存储、传送和交换过程的安全性,是保证信息安全的有效措施.同时,为了减少存储空间、降低传输带宽,就需要对原始数据进行高效的压缩.Shennon指出[1],冗余度越小,相关性越小,不确定度越大,破译难度越大,安全性就越高.传统的先压缩后加密的方法灵活性低,计算量大,实时性差.一种解决方法就是将压缩与加密同步实现.相对空域加密,变换域加密具有更强的鲁棒性.基于离散小波变换(discrete wavelet transform,DWT)平台的比特平面编码,如内嵌零树小波编码(EZW)[2]和JPEG2000标准[3]已被证实能够获得好的图像压缩效果,且DWT变换是对图像的全局变换,不会出现离散余弦变换(discrete cosine transform,DCT)的方块效应.当前加密领域的研究主要是对空域数据的单纯加密或基于简单的非自适应的熵编码进行加密[4-8].因其所使用的熵编码器模型简单,算法复杂度较低,在不进行明文或密文置换条件下,很容易受到攻击[6].文献[9]提出采用分组密码系统在非线性有限域小波变换子带上加密,但没有研究算法的压缩特性.文献[10]提出一种基于Logistic映射的分组加密系统,将Logistic映射产生随机二进制序列分成两部分,一部分用于对明文的置乱,另一部分再与置乱明文进行简单的异或运算产生密文,但在加密过程中没有进行密钥流与明文的相关,使得该算法在明文攻击时显得很脆弱.文献[11]提出了一种基于多级树集合分割算法(set partitioning in hierarchical trees,SPIHT)的感知加密,通过置换同一父系数的四个子系数的位置进行加密,但没有考虑子带间相关性,致使压缩效率不高.文献[12]研究了在小波变换与SPIHT编码之间进行加密,因加密发生在量化和压缩之前,在有损压缩中鲁棒性极差且影响压缩效率.本文提出了一种新的简单有效的基于EZW的图像压缩和树形加密同步算法.该算法充分利用EZW编码的渐进式传输特性和树形结构,利用Logistic映射生成的密钥对比特平面编码过程中产生的上下文和系数进行修正,再采用高压缩率的MQ算术编码进行熵编码,并将密文反馈给Logistic映射实现密钥流与明文相关,因加密发生在比特平面编码与熵编码之间,无需进行数据置换且不破坏小波子带系数之间的相关性,故算法对压缩性能无影响,并能够在实现图像数据压缩的同时,也实现算术加密.实验结果表明,算法具有良好的压缩效率和安全性.
2 EZW编码简述
Shapiro提出的内嵌零树小波编码算法(EZW)[2]利用子带系数之间的相似性,取得了高效压缩效率,即将小波变换后各级HLK,LHK,HHK子带系数构成一棵树,如图1所示.编码每次都从最低分辨率系数开始扫描,如果一棵树的根及其子孙的小波系数的绝对值都小于某个给定的阈值(threshold,T)(这棵树称为零树),可以用一个预定义的符号代表整棵树,从而提高压缩比.
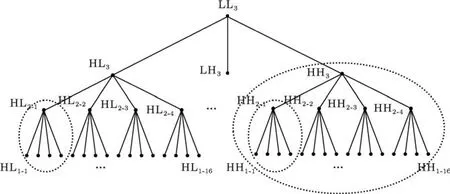
图1 零树结构
本文算法为每棵树分配一组密钥,在比特平面扫描过程中,利用密钥对每个系数产生的上下文(context,CX)和判决 (decision,D)进行修正,再送往算术编码器进行进一步压缩.这种编码方式既实现了分辨率压缩,又达到树形加密的目的.
3 MQ编码器及加密可行性分析
算术编码的最主要优点是输出的码长能逼近信源的熵,因此广泛应用于各种压缩算法,如JPEG,JPEG2000,JBIG和H.264等.MQ算术编码是一种基于上下文的自适应二进制算术编码(context based adaptive binary arithmetic coding,CABAC),是对无乘法器的Q编码算法的改进,增加了条件交换和概率估计状态机中的贝叶斯学习过程,采用Q编码的位填充策略.与比特平面编码相结合,编码从最高有效位(most signi ficant bit,MSB)平面开始到最低有效位(least signi ficant bit,LSB)平面结束,按一定的顺序扫描每个位平面,生成编码数据对(CX,D),再经MQ编码输出压缩的码流,如图2所示.

图2 MQ编码器输入输出模型
MQ编码器采用一种对原始数据快速自适应概率估计模型.输入数据流中的信源符号被分成大概率符号(more probable symbol,MPS)和小概率符号 (less probable symbol,LPS),把 LPS 的概率记作Qe,CX用于估计D出现的概率.通过查索引表得到索引I(CX)和MPS,若D=MPS,表明概率估计正确,进行CODEMPS编码,如(1)式所示,否则表明概率估计错误,进行CODELPS编码,如(2)式所示.并通过及时的重整化(renormalization)操作,编码间隔A始终保持在区间[0.75,1.5]之间,MQ编码简化模型如图3所示.

图3 MQ编码器算法流程图
因为不同上下文CX对应判决D的初始分布不完全相同,而且后续输入判决D的条件概率分布也不完全相同.对于给定的序列,如果上下文CX不同,对应的概率子空间也不相同,编码输出的码字也不相同.如果改变给定序列中的任何一个上下文CX或者判决D,就会导致概率子空间的不同,并会对后续判决的条件概率分布产生影响.因此,使用密钥对上下文CX或者判决D进行修正便可以实现压缩和加密同步进行.
若 D=MPS,则

若 D=LPS,则

4 Logistic映射与密钥的生成
4.1 伪随机序列的产生
混沌现象是非线性动力系统中一种确定性的类随机过程,该过程具有对初始值敏感、遍历等基本特性,相对工作在有限离散集上的传统密码系统,混沌系统工作在无限的连续实数集上,而这些都是一个好的密码系统所期盼的[1],因此被广泛应用于加密技术[13-16].本文使用Logistic映射产生混沌轨道[10,17],如(3)式所示.其中µ为分岔参数,当µ>3.57时,Logistic映射处于混沌状态.
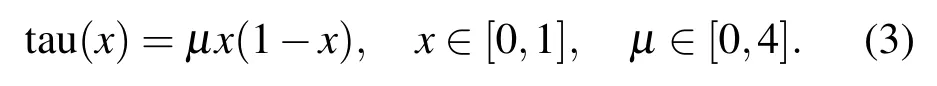
轨道上的每个点采用二进制表示为
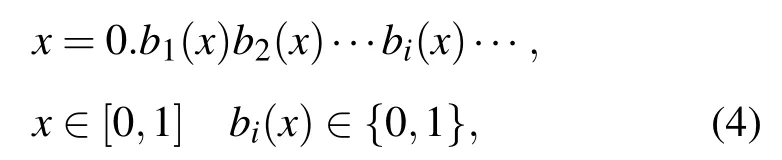
其中bi(x)可通过下式得出

上式中Θt(x)是一个门限函数,其定义如下
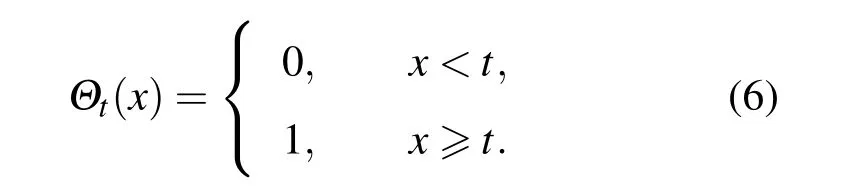
通过式(3)—(6)式便可得到具有独立均匀分布的伪随机序列其中n是二值序列的长度,τn(x)是Logistic映射第n次迭代时的值.
4.2 密钥的生成
在本文算法中,x1,x2,···,xK,xK+1是以双精度浮点型格式表示的Logistic映射的秘密初始值(K为小波分解级数),这些值被用来为图1所示的树形结构每一层节点生成一个32位二进制密钥Key.将xi(i∈[1,K+1])迭代32次并得到32个数据xi1,xi2,···,xi32.利用4.1节的方法产生二进制序列
为了保证加密的安全性及加密和解码双方同步,本文在加密过程中采用了密文反馈的形式与密钥流相关.具体实现的方法是对MQ编码器每生成一字节的码流,便用该字节码流对当前密钥重新进行迭代,以生成新的密钥,如下式所示:

其中Cnum为当前字节密文,R为要迭代次数.迭代完成后得到R个数据xi1,xi2,···,xiD,从中抽取32个数据生成 32 位二进制序列
5 图像压缩和树形加密的实现方法
本文提出的基于EZW的压缩和树形加密同步算法原理如图4所示.原始图像经DWT变换后将原图数据的相关冗余映射成为小波系数的统计冗余,再进行EZW编码.在比特平面编码过程中生成原始编码数据对(CX,D),用密钥Key对CX和D分别进行修正,产生修正数据对(CX1,D1),并送往MQ编码器进行熵编码,最后输出压缩的码流,从而实现图像压缩和按树形结构加密.
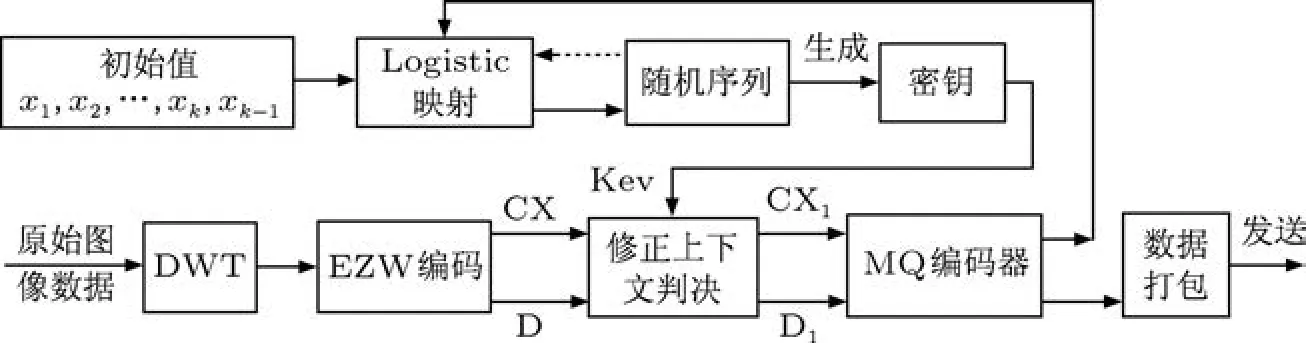
图4 基于EZW图像压缩和树形加密原理框图
为使MQ编码器获得良好的编码效率,将比特平面编码过程中按所使用的是相邻系数或相邻集合的重要性对产生的判决进行了分类以形成上下文.由于比特平面编码的判决有两种(即集合判决和系数判决),与之相应的将上下文也分为集合上下文和系数上下文两种.
集合上下文的计算,本文采用简单的同分辨率相邻集合重要性产生,如图5所示,A表示当前集合重要性,D0,D1,D2,D3表示对角相邻集合重要性,H0,H1表示水平方向相邻集合重要性,V0,V1表示垂直方向相邻集合重要性,它们的取值为{0,1}(其中0代表集合不重要,1代表集合重要).8个周边集合共形成256种上下文,经合并形成4种集合上下文.集合上下文CXs的计算公式为
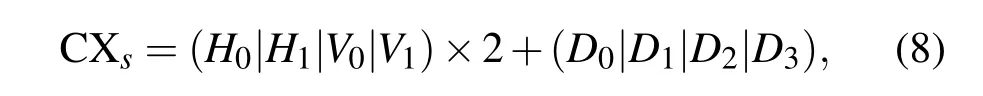
其中“|”表示或运算.显然CXs取值为{0,1,2,3}.
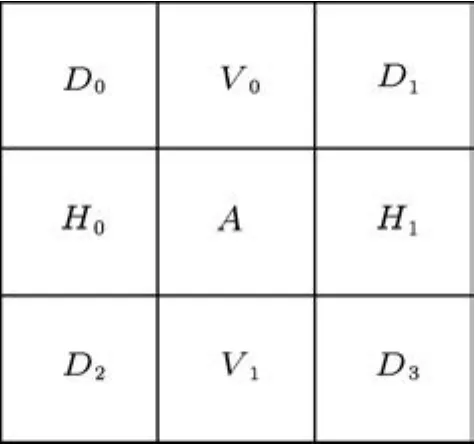
图5 集合A的相邻集合
系数上下文的计算采用最佳截断嵌入码块编码(embedded block coding with optimized truncation,EBCOT)中的方法[18-21]进一步细化为零编码上下文、幅值上下文、符号编码上下文,限于篇幅不再赘述.
基于判决修正的算术加密原理如下:
利用密钥对位平面产生的二进制判决进行某种运算,使得修正后的判决与原始判决不同,只有当系统编码和解码使用相同的密钥流时才能解码正确,否则解码错误,从而实现了判决加密.
设 Key 表示加密密钥流,D=(d1,d2,···,dN)表示编码产生的原始二进制判决矢量,长度为N,定义一种运算
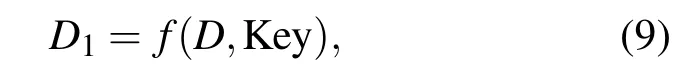
其中 D1=(d11,d12,···,d1N) 为修正后的二进制判决矢量,长度也为N.
设Key1表示解密密钥流,表示解码后的判决矢量,当Key1=Key时,则=D,即当解密使用相同密钥流时,将正确重建原始判决序列,于是下式成立:

其中 f-1为(9)式对应的逆运算,所以(9)式定义的运算对密钥流应是可逆的.
基于上下文修正的加密方法如下:
设MQ编码器的上下文范围为(m,m+1,···,m+Lm),设 Key 为加密密钥流,CX 为原始上下文,取值范围为 (m,m+1,···,m+L),CX1为修正后的上下文,取值范围为 (m,m+1,···,m+L′),上下文修正可以表示为

其中g(·)表示定义的某种变换,n表示该类上下文出现的顺序,L与L′分别表示CX和CX1的种类,且有L<Lm,L′<Lm.(11)式需要满足如下要求:
1)对应给定CX和Key,对于不同的n(即在编码的不同时刻),(11)式运算的修正上下文不能总是固定值,即CX1是CX和Key的非线性运算,否则不能实现算术加密.
2)在加密和解密过程中,若比特平面编码和解码生成的上下文CX相同,且使用相同的变换和相同密钥流对CX进行修正,则送往MQ编码器的修正上下文CX1相同,从而得到正确的解码.即在加密和解密过程使用相同的运算可保证正确解密,故(11)式可以是不可逆运算.
3)因为MQ编码使用的各类上下文范围一定,如果超出MQ编码使用的某类上下文范围,则进入其他类别的上下文范围.而不同类别的上下文所对应的初始概率分布不同,条件概率的跳转规律也不相同,进行联合压缩加密时,可能会导致重建图像质量下降.所以CX1不能超过算术编码所对应类型的范围,否则可能导致压缩的效率下降.
在本文中,判决修正采用简单的异或运算,对密钥流Key进行循环移位得到密钥流Key1,即首先利用Key的最低位与原始判决进行异或运算,再将密钥循环移位一次得到Key1,以供下一次判决修正使用.
上下文修正算法是对密钥流Key进行循环移位,取移位后的最低若干位二进制数据dk与CX(范围为 (m,m+1,···,m+L))按下式运算:
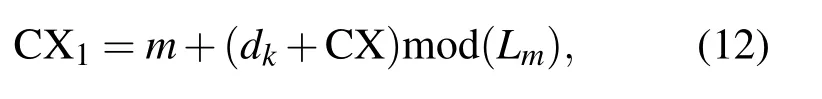
其中 mod(·)表示模运算.CX1范围为 (m,m+1,···,m+Lm).该算法能够满足上文所提的上下文修正的三条要求.
结合EZW的比特平面编码,对整个小波域系数按树形结构扫描顺序进行加密,能够实现图像压缩和树形加密同步进行.
6 实验结果与分析
实验中采用 (9,7)不可逆浮点 DWT变换,分解级数为K=3,共需4个Logistic映射初值x1,x2,x3,x4,分别被用来为图1所示的树形结构每一层节点生成一个32位二进制密钥Key,用其对在比特平面编码过程中生成的数据对(CX,D)分别进行修正,以产生修正数据对(CX1,D1),并送往MQ编码器进行熵编码,最后输出压缩的码流,从而实现图像压缩和按树形结构加密同步进行.随机选择的4个初始值如下:

6.1 重构图像的视觉质量
采用标准 8位灰度级图像 (Lena,Airplane,Barbara,Boat,Baboon)进行测试,在 (12)式中取L=Lm,表1中显示当图像压缩8倍,输出码率分别为 0.5 bpp,0.75 bpp,1.00 bpp,1.25 bpp,1.50 bpp时的测试结果.图6显示了在码率为0.5 bpp时重构图像.结果表明,在相同码率下,本文算法与原始EZW算法重构图像质量基本相同,即具有相同的压缩效果.
6.2 密钥空间
一个好的加密算法应该对密钥敏感,密钥空间应该足够大来抵抗穷举攻击.本文提出的算法密钥空间大小估计如下:
在K级DWT分解过程中共得到3×K+1个小波子带.小波子带的宽度或高度为M/2l(M为原始图像的宽或高,l为所在的级),正如在4.2节所描述的,为图1中第一棵树的每一层节点分配32 bit的密钥作为初始值,共32×(K+1)bit.MQ编码每输出1Byte压缩码流,便对密钥重新迭代一遍,即密钥是与密文相关的,对一幅大小为M×N的图像,其编码字节数约为2「log2(M×N)⏋,所以算法总的密钥空间是 32×(K+1)×2l「log2(M×N)⏋bit.当 K=3,图像大小为512×512时,密钥空间将达225bit.因此,算法拥有足够长的密钥空间.
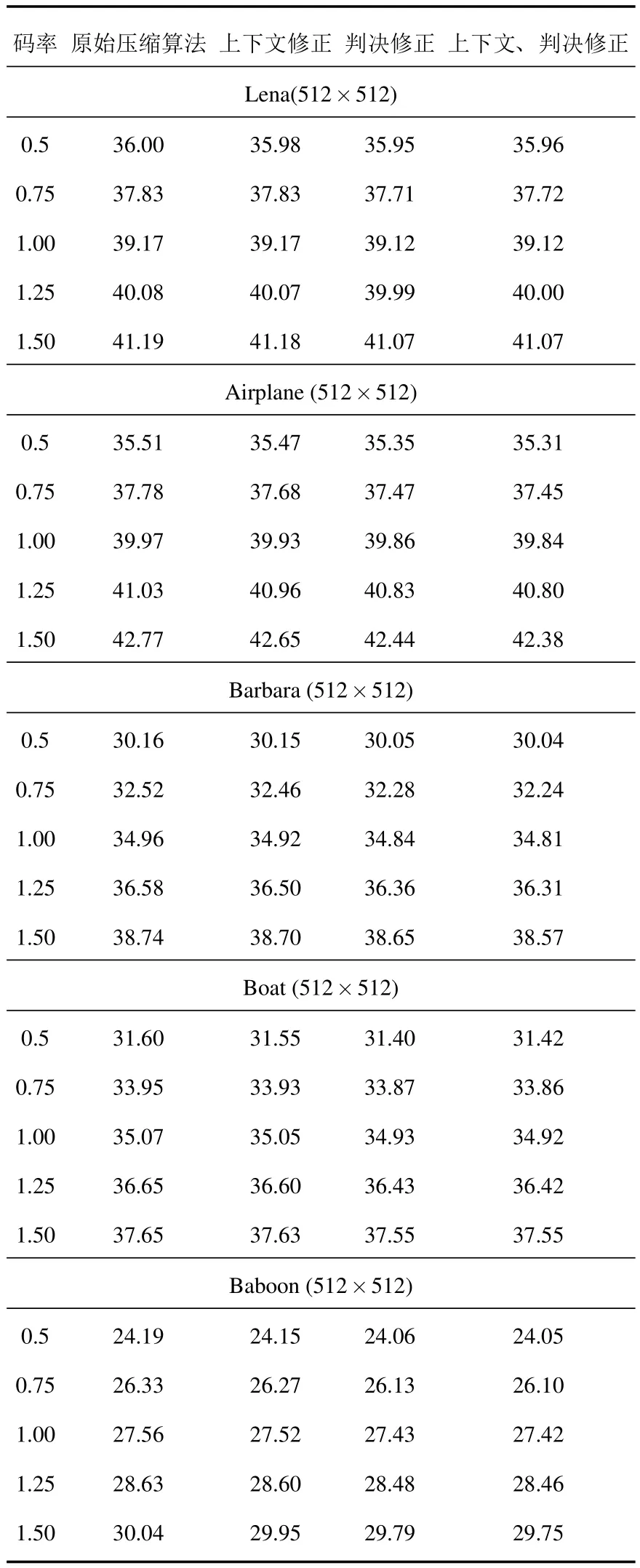
表1 原始算法与本文算法重构图像质量PSNR(单位dB)比较

图6 视觉质量比较 (a)原图;(b)只压缩;(c)上下文修正;(d)判决修正;(e)上下文、判决修正;(f)解密错误
6.3 抗线性攻击与差分攻击分析
6.3.1 密钥敏感性测试
对密钥作一微小改变以测试密钥敏感性,即将Logistic映射初始值小数点最后1位加1或减 1,再进行压缩和加密.测试中仅将x1=0.764350394698857改为 x1=0.764350394698858,其他初始值不变.然后对密文进行逐位比较,并计算其bit变化百分比.如表2和表3所示.结果表明,在不同码率下,位变化百分比都在50%左右,这表明密文对密钥是敏感的.
6.3.2 明文敏感性测试
由(7)式可知,参数R通过密文反馈与明文相关,不同的明文使Logistic映射在加密过程中迭代不同次数,从而产生不同的密钥流.为了测试明文敏感性,随机选取两幅不同的图像(限于篇幅本次测试只给出Lena图像和Barbara图像上下文和判决同时修正的密钥流对比),进行同步压缩加密,产生相应的密钥流,如表4所示.可以看出,从第二组开始密钥就不相同,迭代次数R也不相同,所以算法对明文敏感的.

表2 Lena图像密钥敏感性测试(bit变化百分比)
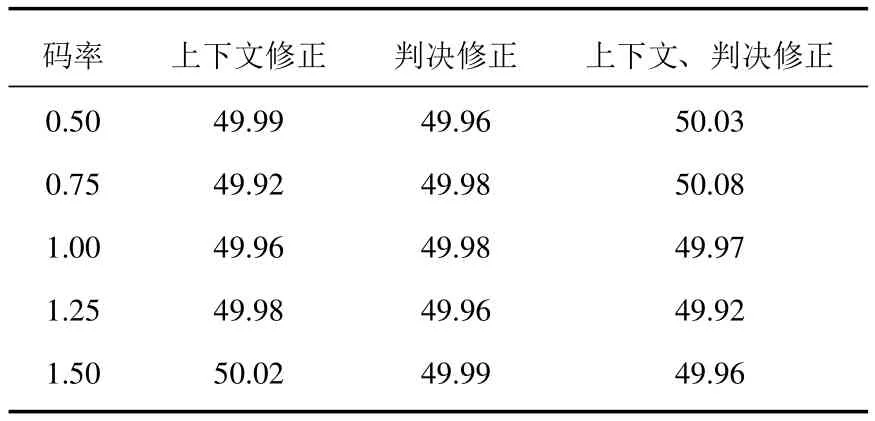
表3 Barbara图像密钥敏感性测试(bit变化百分比)
以上测试表明,密文对密钥和明文都很敏感,从而能够很好的抵抗差分攻击和线性攻击.
6.4 加密与解密速度
表5中列出了Lena图像在不同码率下的编码和解码时间(表中“加密时间”表示加密时间占总时间的百分比).从表中可以看出,随着码率的增大,总的编解码时间也随之增加.加密时间占整个算法时间的百分比均小于50%,即加密时间不会超过压缩时间,这种通过牺牲部分运算来达到良好的压缩加密效果是非常值得的.
6.5 与其他压缩和加密算法比较
表6中列出了本文算法与文献[12]中SPIHT+SHA-1同步加密算法及JPEG+AES先压缩后加密算法的实验比较结果.实验结果表明,当码率较低时,本文算法重构图像质量要好于SPIHT+SHA-1算法和JPEG+AES算法,这主要是因为SPIHT+SHA-1算法先对小波系数加密再量化压缩致使各分辨率子带系数相关性被破坏导致压缩效率降低引起;而JPEG+AES算法中主要是DCT变换的块效应引起的.本文算法加密时间占算法总时间百分比较高,因为本文加密算法是对整个压缩码流进行了加密,并且密钥流与明文相关.

表4 Lena图像和Barbara图像部分密钥流
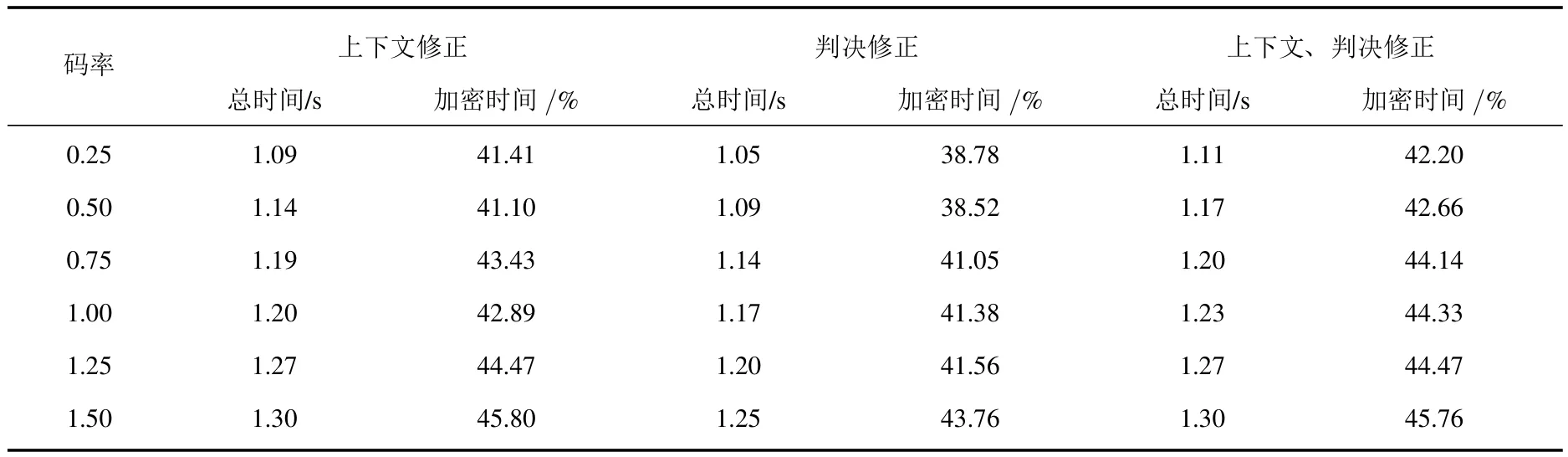
表5 Lena图像加密和解密速度
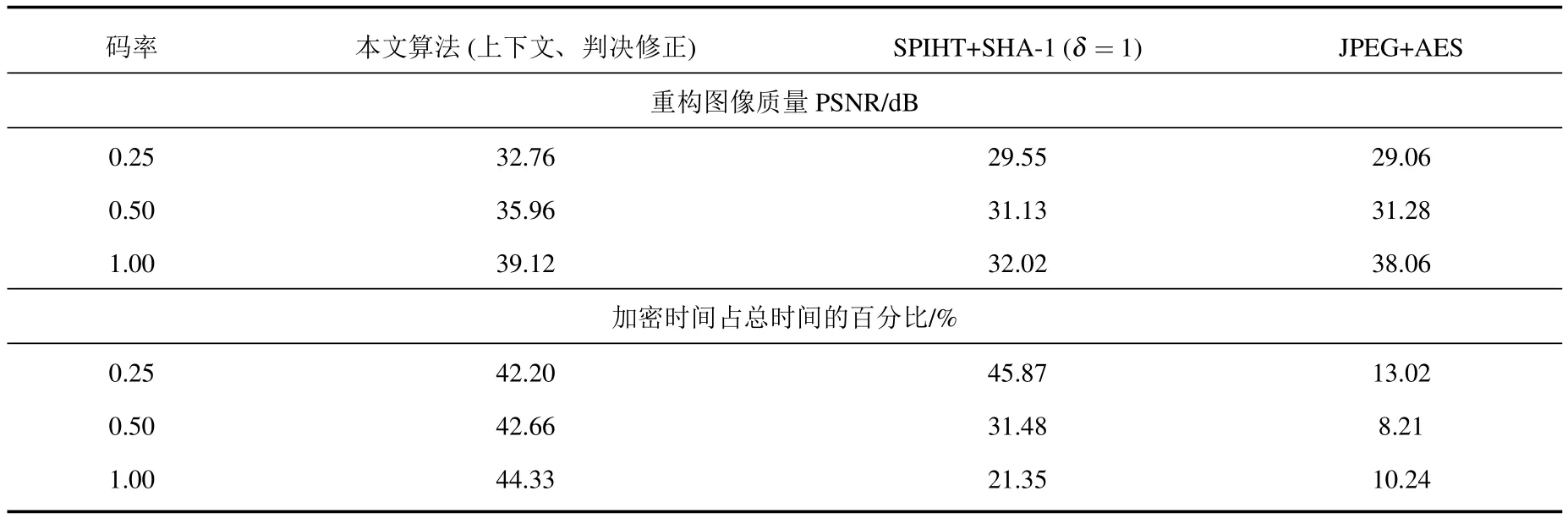
表6 本文算法与其他算法重构图像质量PSNR的比较
7 结论
通过以上分析和仿真表明,本文提出的压缩和树形加密同步算法密钥流与明文相关,因加密发生在比特平面编码与熵编码之间,故算法能够在实现图像数据压缩的同时,也实现算术加密.实验结果表明,加密算法对压缩效率几乎没有影响,且安全性非常好,有很大的密钥空间,对差分攻击和线性攻击具有良好的免疫性具有良好的应用前景.
[1]Shannon C E 1949 Bell System Technical Journal 28 656
[2]Shapiro J M 1993 IEEE Trans.Signal Processing 41 3445
[3]Christopoulos C,Skodras A,Ebrahimi T 2000 IEEE Trans.Consumer Electronics 46 1103
[4]Katti R S,Srinivasan S K,Vosoughi A 2011 IEEE Trans.Information Forensics and Security 6 19
[5]Duan L L,Liao X F,Xiang T 2010 Acta Phys.Sin.59 6744(in Chinese)[段黎力,廖晓峰,向涛2010物理学报59 6744]
[6]Kim H,Wen J T,Villasenor J D 2007 IEEE Trans.Signal Processing 55 2263
[7]Wen J T,Kim H,Villasenor J D 2006 IEEE Signal Processing Lett.13 69
[8]Bose R,Pathak S 2006 IEEE Trans.Circuits Syst.I 53 848
[9]Chan K S,Fekri F 2004 IEEE Trans.Signal Processing 52 2795
[10]Xiang T,Liao X F 2006 Physics Letters A 349 109
[11]Lian S,Sun J,Wang Z 2004 IEEE Int.Conf.Multimedia Expo 3 2195
[12]Yang H Q,Liao X F,Wong K W,Zhang W,Wei P C 2012 Acta Phys.Sin.61 040505(in Chinese)[杨华千,廖晓峰,Wong K W,张伟,魏鹏程2012物理学报61 040505]
[13]Zhou W J,Yu M,Yu S M,Jiang G Y,Ge D F 2012 Acta Phys.Sin.61 080701(in Chinese)[周武杰,郁梅,禹思敏,蒋刚毅,葛丁飞2012物理学报61 080701]
[14]Liu Q,Fang J Q,Zhao G,Li Y 2012 Acta Phys.Sin.61 130508(in Chinese)[刘强,方锦清,赵耿,李永2012物理学报61 130508]
[15]He T T,Luo X S,Liao Z X,Wei Z C 2012 Acta Phys.Sin.61 110506(in Chinese)[何婷婷,罗晓曙,廖志贤,韦正丛2012物理学报61 110506]
[16]Sun K H,He S B,Yin L Z,Duo L K 2012 Acta Phys.Sin.61 130507(in Chinese)[孙克辉,贺少波,尹林子,阿地力·多力坤2012物理学报61 130507]
[17]Yang J Y,Liao X F,Xiao D 2008 Journal on Communications 29 86(in Chinese)[杨吉云,廖晓峰,肖迪2008通信学报29 86]
[18]ISO/IEC JTC 1/SC 29/WG1 FCD 14495 public draft,1997-06.http://www.jpeg.org/public/jpeglinks.htm.
[19]Taubman D 2002 IEEE Trans.Image Processing 9 1151
[20]Taubman D,Ordentlich E,Weinberger M,Seroussi G 2002 Signal Processing:Image Communication 17 49
[21]Deng J X,Wu C K,Chen J 2004 Acta Optica Sinica 24 299(in Chinese)[邓家先,吴成柯,陈军2004光学学报24 299]

