飞秒脉冲激光对纳米金属薄膜传导模型的解*

韩祥临 赵振江 程荣军莫嘉琪3)

1)(湖州师范学院理学院，湖州 313000)

2)(浙江大学宁波理工学院，宁波 315100)

3)(安徽师范大学数学系，芜湖 241003)

(2012年11月20日收到;2013年1月18日收到修改稿)

1 引言

当前超短波脉冲激光技术正在迅速的发展，已经可以达到阿秒(10-18s)量级.飞秒(量级10-15s)的激光器已经十分成熟.它在激光受控核聚变、高密度信息存储、精密器件加工、医学外科手术等领域都有广泛的应用.同时超短脉冲技术的加工，由于有能耗低、加工精确、避免附加热损耗等特点，因而广泛地应用在精密加工方面.对于异质结场效应晶体管等微电子器件在超高频率运行时，由于电子和声子将处于非平衡状态，这将使微器件的热阻增大，导致为电子器件的温度升高，从而严重影响器件的工作性能，因此需要对电子和声子超短脉冲激光加热金属薄膜的导热温度的研究，以寻求转化电子和声子温度达到平衡过程.但其机理很为复杂，目前学者已做了许多工作[1-6].又因不同的模型只适用于描述超短脉冲激光加热金属薄膜的不同阶段，而不能采用一个统一的模型描述完整的热量扩展过程.所以目前对纳米薄膜材料性质的研究，特别是瞬间导热的研究，采用了超快速激光反射方法的实验.王海东等利用飞秒激光热反射/透热系统测量了金属/半导体薄膜的反射率随时间的变化[5].然而，目前对超短波脉冲飞秒激光传导的理论分析，也在同步研究，特别是用解析的方法来得到模型解的解析表达式，并通过数学解表示式对模型的各物理量性态作进一步的解析分析.本文就是建立一个普适模型用于描述超短脉冲激光加热薄膜的整个导热过程的双温度模型，其实验装置示意图如图1所示[1,5,6]，并用渐近方法得到其近似解析解.非线性问题在国际学术界是一个十分关注的对象.近来，很多学者做了许多工作[7-12].一些近似方法也被优化，包括合成展开法，边界层法，匹配法，多重尺度法等.作者等也研究了一些非线性问题，得到了相应问题解的渐近表示式[13-18].本文是利用数学的解析方法来研究一类飞秒脉冲激光电子和声子控制导热模型，并求出其渐近解析解.

2 飞秒脉冲激光传导模型及其退化解

讨论如下一类飞秒脉冲激光电子和声子控制导热模型[5,6]：

其中Te,Tl分别为电子与声子温度，γ,Cl分别为电子与声子热容，keq为初始温度下电子的导热系数，G为电子-声子耦合系数，S为激光及热过程转化为热源项

不妨选取参数为：R=0.57，kep=1，J=1 mW，tp=0.96 J·m-2，l=2 nm，γ=0.95×106J·m-3·K-2，δ =0.5 nm，T0=1°C，Cl=1×106J·m-3·K-1. 由(9)，(10)式可得飞秒脉冲激光退化系统(5)—(8)的电子温度Te0(x,t)的扩散分布如图2所示.

图1 飞秒激光的系统实验装置示意图

图2 飞秒脉冲激光退化系统电子温度Te(x,t)的扩散分布图

显然，飞秒脉冲激光电子和声子控制系统(5)—(8)的退化解(9)，(10)式，并不是飞秒脉冲激光电子和声子控制系统导热模型(1)—(4)的解.为此我们还需构造系统的渐近解.

3 飞秒脉冲激光传导模型的渐近解

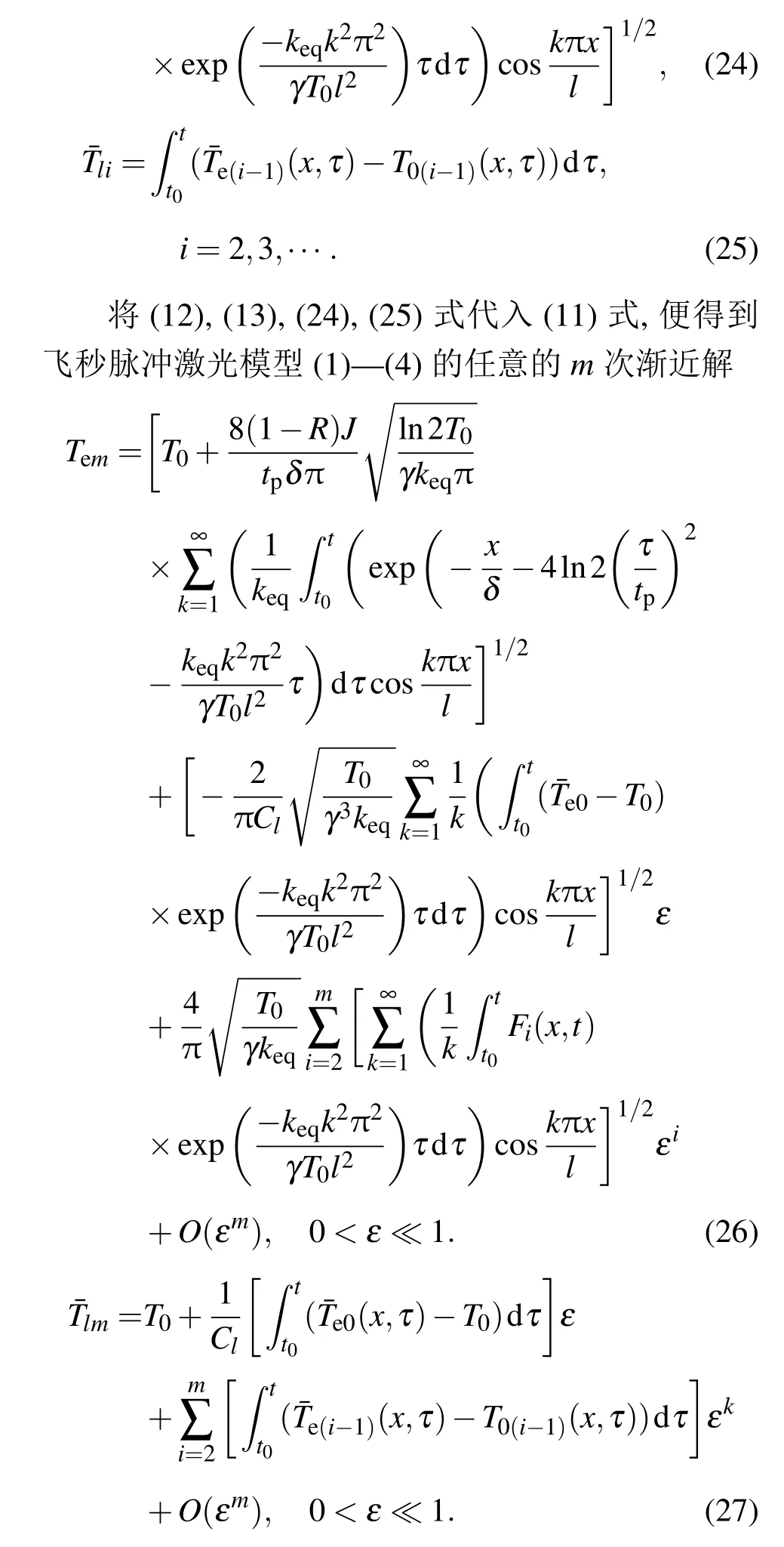
我们还可证明[7,8]，在(26)，(27)式中，取m→∞时，便为飞秒脉冲激光电子和声子控制导热模型(1)—(4)的精确解.

4 飞秒激光传导模型渐近解的模拟图

现考察飞秒脉冲激光电子和声子控制导热模型(1)—(4)，仍选取相应的参数为

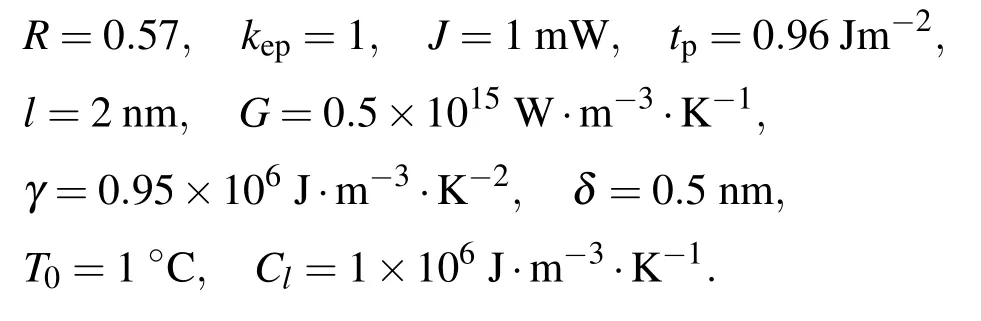
由 (9)，(10)，(24)，(25) 式得飞秒脉冲激光系统(1)—(4)的电子和声子温度关于ε的一次渐近解(Te1(x,t),Tl1(x,t))的扩散分布如图3和图4所示.

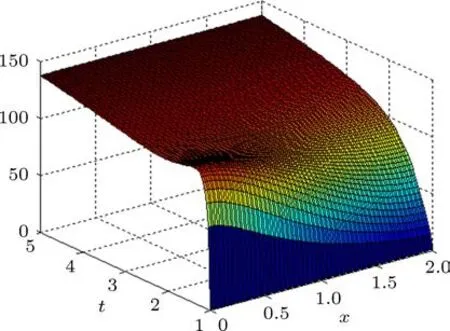
图3 飞秒脉冲激光系统电子温度一次渐近解Te1(x,t)的扩散分布图

图4 飞秒脉冲激光系统声子温度一次渐近解Tl1(x,t)的扩散分布图

利用渐近解(18)，(19)式和上述模拟图，可以分析和观察到脉冲激光电子和声子温度的峰值、通量和其他物理量的趋势等性状，得到的结果完全符合其规律.并证实了在超短脉冲激光超快加热薄膜的过程中，由于电子和声子将处于非平衡状态转化电子和声子温度达到平衡过程.从渐近解(18)，(19)式和上述模拟图，还可调整飞秒速度及脉冲激光强度和其他有关参数，使得导热模型达到最佳状态.由上述的分析、计算过程，特别是用解析的方法来得到模型解的解析表达式，并通过数学解析表示式对模型的各物理量性态作进一步的解析分析.使得对问题有一个更深刻的了解。

由上述提供的方法还可继续得到更高次的渐近解，并可画出它们的模拟图.再经过研讨，可得到更精确的结果，使得模型的分析与实际情况更接近，从而能得到更满意的结果.关于方面的讨论，在此不再进一步论述.

5 结论

本文是用数学理论和方法来求解飞秒脉冲激光对钠米金属薄膜导热模型得到的近似解.它可以对相应模型的实验结果作比较，以此作为改进加工技术的依据.超短波脉冲激光加热传导是当前的一个尖端技术，它在许多领域中被广泛地应用.许多学者正致力于开发更多的技术范围.因此需要研究相关的理论，其中就需要用数学理论的方法得到有关模型的近似解.本文就是在这方面的一个探讨.模型解的渐近解析表达式.所用的是渐近方法可得到任意次精度的近似解.这种方法直观明确，并且还可以继续用微分、积分的数学解析工具来得到更多相关物理量的性态.因此在方法上很具有很广的前展性..

[1]Xin Z L，Fan Z X，ShaoJ D 2006 Acta Phys.Sin.55 3007(in Chinese)[夏志林，范正修，邵建达2006物理学报55 3007]

[2]Eesley G L 1983 Phys.Rev.Lett.51 2140

[3]Qpu T Q，Tien C L 1993 J.Heat Transf.Trans.ASME 115 835

[4]Xiong G C，Zou Y H，Xin Z J，Yuan P，Lian G J，LiJ 1994 Acta Phys.Sin.43 1860(in Chinese)[熊光成，邹英华，夏宗炬，袁平，连贵君，李洁1993物理学报43 1860]

[5]Ma W G，Wang H D，Zhang X，Wang W 2011 Acta Phys.Sin.60 064401(in Chinese)[马维刚，王海东，张兴，王玮2011物理学报60 064401]

[6]ZhuLD，SunFY，ZhuJ，TangDW2012ActaPhys.Sin.61130512(in Chinese)[朱丽丹，孙方远，祝捷，唐大伟2012物理学报61 130512]

[7]de Jager E M Jiang Furu 1996 The Theory of Singular Perturbation(Amsterdam：North-Holland Publishing Co)

[8]Barbu L，Morosanu G 2007 Singularly Perturbed Boundary-Value Problem(Basel：Birkhauserm Verlag AG)

[9]D’Aprile T，Pistoia A 2010 J.Differ.Eqns.248 556

[10]Ei，Shin-Ichiro，Matsuzawa H 2010 Discrete Contin.Dyn.Syst.26 910

[11]SuzukiR 2010 Adv.Differ.Eqns.15 283

[12]Deng S B 2012 J.Differ.Equations 253 727

[13]MoJ Q 1989 Science in China Ser A 32 1306

[14]MoJ Q 2008 J.Sys.Sci.&Complex 20 119

[15]MoJ Q 2009 Science in China Ser.G 52 1007

[16]MoJ Q 2009 Chin.Phys.Let.26 010204

[17]MoJ Q 2010 Commun.Theor.Phys.53 440

[18]MoJ Q，Lin Y H，Lin W T 2010 Chin.Phys.B 19 030202