两相流有限穿越可视图演化动力学研究*
高忠科 胡沥丹 周婷婷 金宁德
(天津大学电气与自动化工程学院,天津 300072)
(2012年12月27日收到;2013年1月27日收到修改稿)
1 引言
在石油、化工及核反应堆等工业领域存在着大量的两相流动现象,例如动力工程中锅炉蒸发管中的蒸汽-水两相流动,化工工业中物料输送管道和反应釜搅拌器中的气液两相流以及石油工程中油田开采油井中的油水两相流和气液两相流等.在两相流动过程中,由于相界面的形状和分布随着时间和空间的改变而变化,且相间存在不可忽略的相对速度,导致相界面呈现出不同的几何形状或流动结构,称之为两相流流型.流型不仅影响混合流体的流动特性、压降特性和传热传质性能,而且还是两相流测量、控制与预测系统的重要参数.因此,揭示两相流不同流型的内在流动特性对两相流工业系统优化设计及工况动态监测具有重要实际意义.两相流系统是具有混沌、耗散、有序与无序等复杂特征的非线性动力学复杂系统[1-3],由于两相流受到诸如流体湍动、相间界面相互作用及相间局部相对运动等许多复杂因素的影响,其流动行为呈现出高度无规则性、多态性和结构不稳定性,至今其流型转变动力学机理尚未十分清楚.两相流流型的实验测量、动态描述、结构识别及演化动力学机理揭示等相关研究已成为多相流研究领域的一个重要方向.
本文针对小管径垂直上升管气液两相流,全新优化设计了弧形对壁式电导传感器,通过动态实验在获取传感器测量信号的基础上,采用我们最近提出的有限穿越可视图理论分析测量信号揭示不同气液两相流流型的内在演化动力学机理.可视图理论属于复杂网络时间序列分析理论的一种,复杂网络理论是对复杂系统的一种抽象和描述方式,所谓网络就是由节点和连边组成,其中节点表示系统的元素,两节点的连边表示元素之间的相互作用.在小世界网络[4]和无标度网络[5]的开创性工作之后,复杂网络理论已成功应用于物理学、生物学、经济学和工程学等多个学科领域的大量复杂系统研究之中,并在相应领域取得了很大进展.近年来,基于时间序列测量信号的复杂网络动力学研究受到了不同领域研究人员的广泛关注[6-19],不同的时间序列复杂网络构建与分析算法相继提出[20-33]并已成功应用于不同的复杂动力学系统研究之中[34-48].值得指出的是,Lacasa和Luque[24-26]等提出的可视图和水平可视图建网方法具有可处理数据量大且计算速度快的优点,从而具备潜在的实时测量数据在线分析能力.我们最近研究发现这两种可视图建网方法虽然可以有效区分和刻画不同类型的动力学信号,但其在实测信号分析中的噪声适应性上存在问题.为此,在可视图建网思想启发下,我们提出了一种有限穿越可视图建网方法[32],通过对三种可视图建网方法(可视图、水平可视图、有限穿越可视图)的比较评价,发现有限穿越可视图不仅可以有效区分具有不同动力学特性的时间序列,同时在两相流实测信号分析上表现出较好的抗噪能力.因此,本文采用有限穿越可视图理论研究小管径气液两相流流型演化动力学机理.此外,需要指出的是我们前期针对内径为125mm的大管径两相流流动特性,提出了不同类型的两相流复杂网络,并将其应用于两相流流型非线性动力学特性研究之中[2,41,42].与前期研究不同,与大管径(125 mm直径)两相流相比小管径(20 mm直径)气液两相流流型动力学演化机理更为复杂,本文针对小管径垂直上升气液两相流全新设计弧形对壁式电导传感器并通过动态实验获取传感器测量信号,在此基础上采用具有可处理数据量大、计算速度快、抗噪能力强等优点的有限穿越可视图理论分析测量信号,研究不同气液两相流流型的非线性动力学特性,尤其是在不同流型演化过程中的细节演化动力学机理.用传统的科学观念和方法研究复杂的两相流动问题仍存在较大局限性,本文从全新理论产生及信息处理技术不断完善的角度采用有限穿越可视图理论认识两相流动现象,从而为研究复杂混相流体流动结构及流动特性提供了一种新的理论工具.
2 弧形对壁式电导传感器设计与两相流动态实验数据获取
为了有效获取内径为20 mm的垂直细管气液两相流不同流型的流动信息,本文采用有限元分析软件ANSYS优化设计了弧形对壁式电导传感器,传感器实物结构图如图1所示,其材质为不锈钢,其中图示半环形电极成对内嵌在测量管道内,构成一组检测电极和两组保护电极,每组电极处于管道径向的同一个截面上且严格对称,管道外侧添加保护层增加传感器机械强度.我们在天津大学油气水多相流流动实验装置上进行了垂直气液两相流的动态实验.油气水多相流流动实验装置可以实现在20 mm管径的树脂管道中进行气相、水相、油相及聚合物的混合流动实验,控制不同相的流量,并对其进行测量.动态实验测量系统主要包括信号调理模块、数据采集模块和数据存储模块.信号调理模块主要由C/V转换电路,整流电路,滤波电路和放大电路四部分构成.数据采集模块选用美国国家仪器(NI)公司基于PXI总线技术的PXI 4472和PXI 6221数据采集卡进行数据采集,采样频率为4000 Hz,采样时间为30 s.数据存储模块采用PC机,通过数据采集卡匹配的图形化编程软件LabVIEW实现,可以对数据进行实时的波形显示和实时存储等功能.

图1 弧形对壁式电导传感器实物图
实验方案为首先固定一个水相流量,然后逐渐增加气量,当气液两相流量均稳定后,观察并记录该工况的流型并利用弧形对壁式电导传感器测量得到每一个工况下的电压波动信号.改变水相流量,重复上述过程,得到一系列对应于不同流型的时间序列测量信号.实验过程中,随着工况的改变,两相流流型也会随之变化.本次实验一共采集到对应于泡状流、段塞流和混状流三种典型流型的多组实验数据,其中水相流量变化范围为0.34—1.29 m/s,气相阀门开度的变化范围为5—25 psi(1 psi=6.895 kPa),水相密度为1.0 g/cm-3.在正弦信号的激励下,气相的变化引起检测电极上的电压信号波动.对应于不同气液两相流流型的弧形对壁式电导传感器测量信号如图2所示.图2(a)为细小泡状流,泡径约1 mm,此时测量信号的细小波动反映了该流型下的小气泡随机运动特性;图2(b)为泡状流,泡径约2—3 mm,此时随着小气泡泡径的增大,测量信号波动变强,表明该传感器能够反映出因泡径变化所引起的流型流动特性的变化;图2(c)为段塞流,液塞与气塞交替出现,高电平信号表示液塞通过测量截面,高电平信号的微小波动表明水相中夹带小气泡,负脉冲信号表明有气塞通过测量截面;增加气相流量,出现图2(d)所示的段塞流,其负脉冲变长,表明随着气相流量增大,气塞变长;图2(e)为混状流,此时测量信号上下振动剧烈,表明该流型中气相与液相上下震荡的不稳定运动特性;增加气相流量,出现图2(f)所示的混状流,此时测量信号以低电平为主,表明在此流动工况下气相运动占优势.因此,弧形对壁式电导传感器对气液两相流型有较高的空间分辨率,能够刻画不同流型下的流体流动细节信息,为深入研究气液两相流流型演化动力学机理提供了可靠有效的信息源.
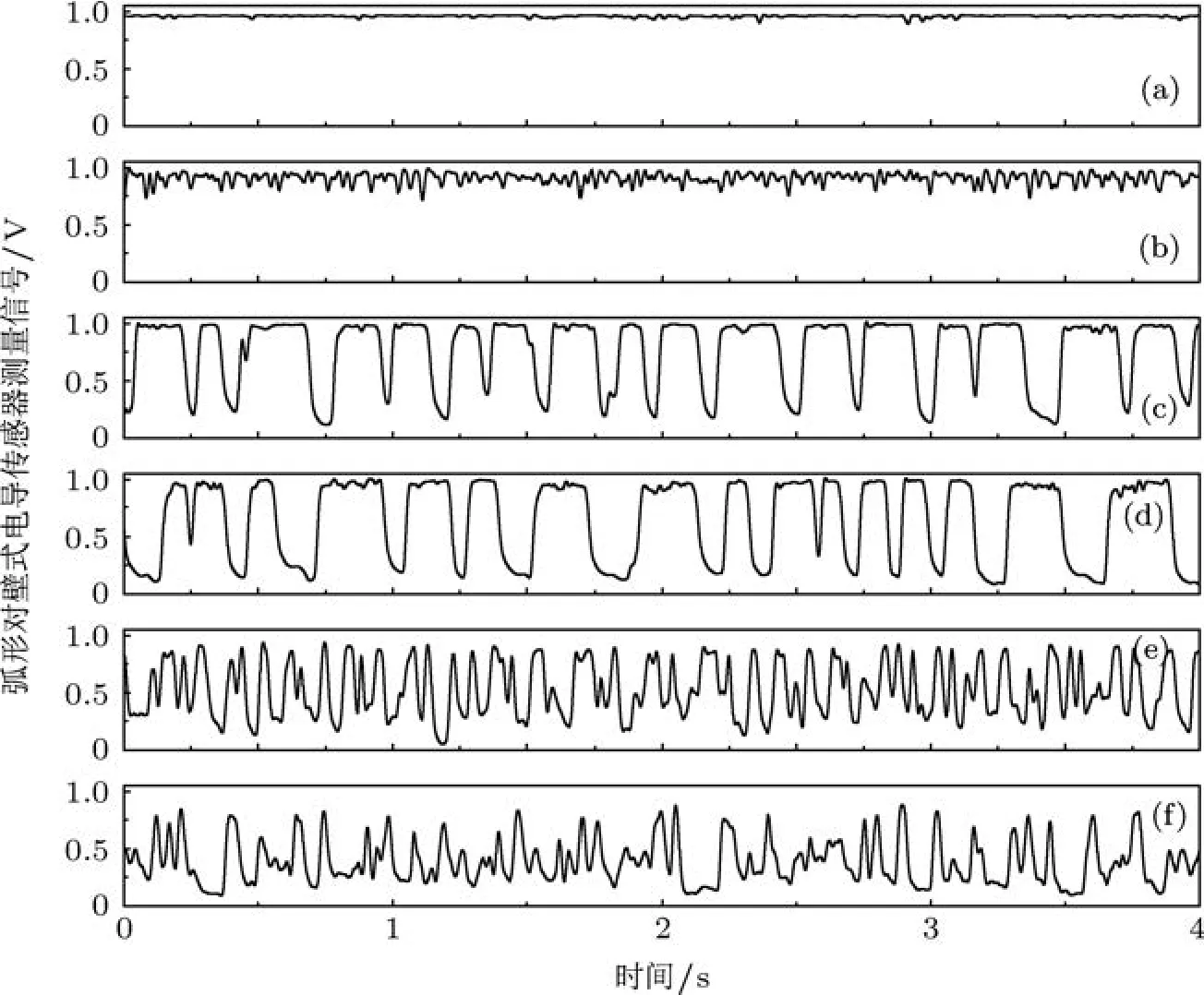
图2 弧形对壁式电导传感器测量信号 (a)泡状流;(b)泡状流;(c)段塞流;(d)段塞流;(e)混状流;(f)混状流
3 有限穿越可视图建网分析算法
受可视图建网方法思想的启发,我们最近提出一种有限穿越可视图建网分析算法,通过对可视图、水平可视图和有限穿越可视图的比较评价,发现有限穿越可视图不仅可以有效区分具有不同动力学特性的时间序列,同时在两相流实测信号分析上表现出较好的抗噪能力.我们如下将简要介绍可视图和有限穿越可视图建网分析算法.
3.1 可视图建网方法
Lacasa等[24]提出了可视图建网方法(Visibility Graph).对于离散时间序列,将数据点定义为网络节点,数据点之间满足可视性准则的连线定义为网络连边.如图3所示,用直方条表示一个周期时间序列中20个数据点(图3(a)),数据真实值与直方条高度相对应.若两个直方条顶端相互可视,则认为两点在网络中相连.图3(b)是由该方法生成的网络,依次排开的实点与离散时间序列数据点一一对应,实点之间的连线与直方条之间的可视线一一对应.值得指出的是,可视线不能重复或者遗漏,节点与自身不能相连,两个直方条之间的可视线不能穿越其他直方条.
可视性准则:如果离散时间序列中点(ta,ya)和点(tb,yb)相连接,那么对于任意的点(tc,yc),其中ta<tc<tb,满足

可视图网络具有如下性质:每一个点至少和它的左邻点和右邻点相连;网络为一个无向无权网络;横轴和纵轴坐标尺度变化或者经过仿射变换后,可视性保持不变.可视图方法能够继承原始时间序列的一些特征,即周期时间序列转化成规则网络,随机时间序列转化成随机网络,分形时间序列转化成无标度网络.

图3 时间序列可视图建网示意图
3.2 有限穿越可视图建网方法
在可视图建网方法思想的启发下,我们最近提出了一种有限穿越可视图建网方法[32](Limited Penetrable Visibility Graph).其基本思想是:定义有限穿越视距N,基于可视图方法可视性准则,规定若网络中的两节点相连,当且仅当与节点相对应的两个直方条之间的连线被位于其间的其他直方条截断次数n≤N.图4为一个有限穿越可视图建网示例,有限穿越视距N=1,图4(a)中,实连接线表示基于可视图方法的连接线,虚连接线表示新增连接线,图4(b)中,实点上方为基于可视图方法的连接线,下方为新增连接线.
有限穿越可视图方法具有连接无向性与仿射变换或者坐标轴尺度变换后可视性不变的特点,每个节点至少和2(N+1)个节点相连.研究发现,在噪声的干扰下,可视图方法中本应相连的节点易受噪声点隔断,对建网效果产生影响,动力学特性被噪声掩盖.由图3和图4可知,有限穿越可视图网络具有更强的连接性,长程连接能够反映序列波动趋势,在有噪声的情况下仍能较好的反映信号的动力学特性.
4 气液两相流有限穿越可视图流型动力学分析
实验中采用弧形对壁式电导传感器测取了对应于不同流动工况的23组测量信号,其中10组测量信号对应于泡状流,4组测量信号对应于段塞流,9组测量信号对应于混状流.选取有限穿越视距N=5,对实验测取的23组电压波动信号进行有限穿越可视图建网分析,获得网络度分布曲线.定义网络节点平均度值为avK,曲线峰值记为Nmax(即具有相同度值节点个数的最大值),以avK为横坐标,Nmax为纵坐标,得到如图5所示的气液两相流有限穿越可视图网络特征参数分布图.由图可见,泡状流平均度值较小,且集中分布在80—130之间,Nmax分布较广泛,在40—180之间;混状流平均度值较高,且分布较广泛,在200—450之间,Nmax较小,在10—60之间;段塞流平均度值和Nmax主要分布在泡状流和混状流的中间区域.我们选取三种流型中有代表性的点进一步揭示不同流型的网络度分布状态.泡状流中选取Nmax较高的工况点(a)和Nmax较低的工况点(b),段塞流选取工况点(c),混状流选取平均度值较低的工况点(d)和平均度值较高的工况点(e),如图5所示.图6为上述所选的对应于不同流型5个工况点的电压波动信号和相应的有限穿越可视图度分布曲线.

图4 有限穿越可视图建网示意图

图5 气液两相流流型点在avK-Nmax特征参数平面分布
图6(a)流型为泡状流,其中气泡泡径约为2—3 mm,测量信号以高电平为主且具有明显的波动.图6(b)流型为细小泡状流,气泡泡径约为1 mm,测量信号有细小的波动.通过比较分析泡状流流型特征和Nmax值发现,随着Nmax值的减小,即由流动工况(a)到流动工况(b)方向,泡径呈现减小趋势,表明有限穿越可视图网络指标可有效刻画两相流流动物理结构细节特征.图6(c)流型为段塞流,其电压波动信号具有拟周期特性,相应度分布图由多个尖峰构成.虽然(b),(c)两点在avK-Nmax特征参数平面位置接近(如图5所示),但是其度分布图截然不同(如图6(b),(c)所示),表明不同流型具有明显不同的度分布特征.图6(d)流型为混状流,其电压波动信号具有明显的上下跳跃特征,因此节点之间相互“遮挡”,节点可视性相对较低.图6(e)流型为减小水相流速时的混状流,此时电压波动信号震荡频率变缓,节点之间“遮挡”减弱,节点具有相对较高的可视性,相应其avK值变大.通过比较分析混状流流型特征和avK发现,随着avK值的增大,即由流动工况(d)到流动工况(e)方向(如图5所示),水相流速呈增大趋势,表明有限穿越可视图网络指标可有效表征两相流流动物理结构的宏观特征.
为了进一步揭示两相流流型演化动力学特性,我们从有限穿越可视图中计算对应于不同流型的异速生长指数,以期通过异速生长指数刻画流型演化动力学复杂性.异速生长尺度的概念最早是在生物学研究领域由West等人于1997年和1999年提出的[49,50],异速生长简单的说就是指不同的身体部分存在着不同的生长速率,尺度关系则是生态学中的核心概念,它以简单的形式量化复杂的系统的一般性特征.在生物学研究中,所有的生物尺度可以用如下异速生长方程来描述:

式中Y为表征有机体生理特征的一个变量,例如新陈代谢速率等,M则是指有机体的大小或者体重,b为尺度幂指数.在许多实际复杂网络研究中都能够发现异速生长尺度率,如食物网络[51],器官代谢网络[52],世界贸易投资网络[53,54]等.复杂网络中的异速生长尺度率主要依赖于网络的二叉树结构.一棵树拥有着一个根节点和许多的分支以及叶节点,所以我们可以把树看作是从根节点到叶节点的所用分支和节点的集合.对于树中的每一个节点i,我们将它的Ai值定义为i节点下属的所有叶节点A值的和再加1,显然最底层叶节点没有子节点,所以它们的A值统一定义为1,计算各节点的A值时是从树的最底层叶节点开始依次递归计算各节点A值,直到根节点为止,如下式所示:

其中 j是i的子节点.树中的每一个节点的C值定义与A值定义相似,我们定义Ci为i节点下属的所有叶节点C值的和然后再加上i节点的A值,其中最底层的节点C值也统一定义为1,计算各节点的C值的方法与A值相似,也是从下往上逐层递归计算,迭代计算过程如下式所示:

其中 j是i的子节点.当一股流从树的根节点到叶节点,那么A值代表着节点的尺寸规模,C值代表着流向节点的流量.根据异速生长方程可知,如果该树满足异速生长尺度关系,那么流量C和尺寸A应该满足幂律关系,即有

其中幂率指数η是网络树的一个很重要的结构参数.链状树和星型树是两种极端的树,通常幂率指数η会介于二者之间,对于链状树其指数η=2,对于星型树其指数η=1,所以异速生长幂率指数范围为:1<η<2.研究发现[55],不是所有的树都满足异速生长尺度关系,对于同一个网络,构造的分岔树不同那么对应的异速生长尺度关系也会不同.一个复杂网络可以构造出不同的分岔树结构,本文从复杂网络中构造的是最小分岔树结构,具体构造过程为:首先通过有限穿越可视图算法得到与时间序列对应的复杂网络,然后找出该网络中度值最大的点作为最小分岔树的根节点,接着找出所有与根节点相连的点作为它的子节点,依次类推,直到整个复杂网络完全转化为最小分岔树为止.通过计算分析,我们发现对应于不同气液两相流流型的有限穿越可视图复杂网络最小分岔树结构都满足异速生长尺度关系,即AC曲线在双对数坐标下满足幂律分布的形式,而可视图复杂网络对应的最小分岔树结构却不具有很好的异速生长尺度关系,即AC曲线在双对数坐标下不具有单一的线性关系,如图7所示,表明有限穿越可视图在气液两相流异速生长指数分析上的优越性.

图6 典型工况点的电压波动信号和有限穿越可视图度分布曲线

图7 不同流型的有限穿越可视图及可视图网络AC数值分布图 (a),(c),(e)为有限穿越可视图对应于三种典型流型的AC数值分布图;(b),(d),(f)为可视图对应于三种典型流型的AC数值分布图

图8 不同流型的有限穿越可视图网络异速生长指数和网络平均度值的联合分布图
对测量的23组电压波动信号进行有限穿越可视图建网并提取相应异速生长指数,异速生长指数η和网络平均度值avK的联合分布如图8所示.由图可见,泡状流、段塞流和混状流流型点分布在avK-η指标参数平面的不同区域,表明有限穿越可视图网络异速生长指数与度分布参数组合对三种流型具有较好识别能力.我们进一步采用自适应最优核(AOK)分布算法[56,57]考察测量信号的时频分布特征,对应于不同流型的AOK时频分布图如图9所示.泡状流中存在着大量的小气泡,泡群运动随机可变,其动力学行为十分复杂,使得泡状流运动频率分布较宽(主要分布在0—40 Hz),但运动能量较低(集中在0—12范围内),如图9(a)所示;在流型从泡状流逐渐向段塞流转变过程中,小气泡的密度不断增大,泡群开始发生聚并形成气塞,气塞与液塞的拟周期交替运动使段塞流动力学行为变得相对简单,如图9(b)所示,与泡状流相比,段塞流频率分布较窄(主要集中于0—10 Hz),能量较高(分布在0—100范围内).相应由图8可见,流型在由泡状流向段塞流演化过程中,网络异速生长指数逐渐增大,在段塞流时达到最大值,很好地表征了在泡状流到段塞流演化过程中的动力学特性,网络异速生长指数越小反映了流体运动频率范围越宽、运动能量越低、流型的动力学行为越复杂.随着气相流量的进一步增加,流型从段塞流转变为混状流,由于流体湍动能量的增强,液体被气体冲碎形成液块,受重力作用在整体上升的同时上下翻滚,使得混状流动力学复杂性高于段塞流,如图9(c)所示,混塞流运动频率高于段塞流,其主要分布在0—20 Hz,运动能量低于段塞流,主要集中于0—70范围内.相应流型在由段塞流向混状流演化过程中,随着网络异速生长指数逐渐减小,表征了气液两相流在由段塞流向混状流演化过程中流体动力学行为复杂性逐渐增大.


图9 典型流型的电导波动信号自适应最优核时频分布图 (a)泡状流;(b)段塞流;(c)混状流
因此,通过上述分析可知,有限穿越可视图的网络异速生长指数和网络平均度值的联合分布可实现对小管径气液两相流的流型辨识;有限穿越可视图的度分布曲线峰值可有效刻画两相流流动物理结构的细节特征;网络平均度值可表征流动结构的宏观特性;网络异速生长指数可揭示两相流流型演化动力学复杂性,为深入地理解气液两相流相间相互作用机理及流动特性提供了参考.
5 结论
针对小管径垂直上升气液两相流全新设计弧形对壁式电导传感器,通过动态实验获取对应于不同流型的传感器测量信号.采用我们最近提出的有限穿越可视图理论从测量信号中构建复杂网络,通过分析构建的对应于不同流动工况的有限穿越可视图网络,发现网络度分布曲线峰值Nmax对两相流泡径大小分布十分敏感,可有效刻画两相流流动物理结构细节特征;网络平均度值avK随着水相流速的增大而逐渐增大,可有效表征两相流流动物理结构的宏观特性;网络异速生长指数η对流体动力学复杂性十分敏感,可揭示不同流型演化过程中的细节演化动力学特性;网络异速生长指数和网络平均度值的联合分布可实现对小管径气液两相流的流型辨识.两相流测量信号的有限穿越可视图分析可为两相流相间相互作用机理揭示及流动特性分析提供新视角、建立新途径.
[1]Daw C S,Finney C E A,Vasudevan M,van Goor N A,Nguyen K,Bruns D D,Kostelich E J,Grebogi C,Ott E,Yorke J A 1995 Phys.Rev.Lett.75 2308
[2]Gao Z K,Jin N D 2009 Phy.Rev.E 79 066303
[3]Li H W,Zhou Y L,Liu X,Sun B 2012 Acta Phys.Sin.61 030508(in Chinese)[李洪伟,周云龙,刘旭,孙斌2012物理学报61 030508]
[4]Watts D J,Strogatz S H 1998 Nature 393 440
[5]Strogatz S H 2001 Nature 410 268
[6]Albert R,Barab´asi A L 2002 Rev.Mod.Phys.74 47
[7]Wang W X,Wang B H,Hu B,Yan G,Ou Q 2005 Phys.Rev.Lett.94 188702
[8]Zheng D F,Hui P M,Trimper S,Zheng B 2005 Physica A 352 659
[9]Pan Z F,Li X,Wang X F 2006 Phys.Rev.E 73 056109
[10]Huang L,Park K,Lai Y C,Yang L,Yang K Q 2006 Phys.Rev.Lett.97 164101
[11]Li X G,Gao Z Y,Li K P,Zhao X M 2007 Phys.Rev.E 76 016110
[12]Pei W D,Chen Z Q,Yuan Z Z 2008 Chin.Phys.B 17 0373
[13]Zhou J,Lu J A,Lu J H 2008 Automatica 44 996
[14]Lu X B,Wang X F,Fang J Q 2010 Physica D 239 341
[15]Zhou T,Kuscsik Z,Liu J G,Medo M,Wakeling J R,Zhang Y C 2010 Proc.Natl.Acad.Sci.USA 107 4511
[16]Guo J L 2010 Chin.Phys.B 19 120503
[17]Duan Z S,Chen G R 2012 Chin.Phys.B 21 080506
[18]Zhang C,Sheng H Z,Li F,Yang H Q,Feng G L 2012 Acta Phys.Sin.61 148902(in Chinese)[张聪,沈惠璋,李峰,杨何群2012物理学报61 148902]
[19]Wang W X,Yang R,Lai Y C,Kovanis V,Grebogi C 2011 Phys.Rev.Lett.106 154101
[20]Zhang J,Small M 2006 Phys.Rev.Lett.96 238701
[21]Zhou C S,Zemanov?L,Zamora G,Hilgetag C C,Kurths J 2006 Phys.Rev.Lett.97 238103
[22]Zhang J,Sun J F,Luo S D,Zhang K,Nakamura T,Small M 2008 Physica D 237 2856
[23]Yang Y,Yang H J 2008 Physica A 387 1381
[24]Lacasa L,Luque B,Ballesteros F,Luque J,Nuno J C 2008 Proc.Natl.Acad.Sci.USA 105 4972
[25]Luque B,Lacasa L,Ballesteros F,Luque J 2009 Phys.Rev.E 80 046103
[26]Lacasa L,Toral R 2010 Phys.Rev.E 82 036120
[27]Xu X,Zhang J,Small M 2008 Proc.Natl.Acad.Sci.USA 105 19601
[28]DongesJF,HeitzigJ,DonnerRV,KurthsJ2012Phys.Rev.Etextbf85 046105
[29]Zou Y,Donner R V,Wickramasinghe M,Kiss I Z,Small M,Kurths J 2012 Chaos 22 033130
[30]Gao Z K,Jin N D 2009 Chaos 19 033137
[31]Gao Z K,Jin N D 2012 Nonlinear Analysis:Real World Applications 13 947
[32]Zhou T T,Jin N D,Gao Z K,Luo Y B 2012 Acta Phys.Sin.61 030506(in Chinese)[周婷婷,金宁德,高忠科,罗跃斌2012物理学报61 030506]
[33]Shimada Y,Ikeguchi T,Shigehara T 2012 Phys.Rev.Lett.109 158701
[34]Fang X L,Jiang Z L 2007 Acta Phys.Sin.56 7330(in Chinese)[方小玲,姜宗来2007物理学报56 7330]
[35]Dong Z,Li X 2009 Acta Phys.Sin.59 1600(in Chinese)[董昭,李翔2009物理学报59 1600]
[36]Li X,Dong Z 2011 Phys.Rev.E 84 062901
[37]Zhou L,Gong Z Q,Zhi R,Feng G L 2008 Acta Phys.Sin.57 7380(in Chinese)[周磊,龚志强,支蓉,封国林2008物理学报57 7380]
[38]Gong Z Q,Wang X J,Zhi R,Feng A X 2011 Chin.Phys.B 20 079201
[39]Gong Z Q,Zhi R,Hou W,Wang X J,Feng G L 2012 Acta Phys.Sin.61 029202(in Chinese)[龚志强,支蓉,侯威,王晓娟,封国林2012物理学报61 029202]
[40]Gao X Y,An H Z,Fang W 2012 Acta Phys.Sin.61 098902(in Chinese)[高湘昀,安海忠,方伟2012物理学报61 098902]
[41]Gao Z K,Jin N D 2009 Chin.Phys.B 18 5249
[42]Gao Z K,Jin N D,Wang W X,Lai Y C 2010 Phy.Rev.E 82 016210
[43]Zhang J,Zhang K,Feng J F,Small M 2010 PLoS Comput.Biol.6 e1001033
[44]Liu C,Zhou W X,Yuan W K 2010 Physica A 389 2675
[45]Shao Z G 2010 Appl.Phys.Lett.96 073703
[46]Gao Z K,Jin N D 2011 Chem.Eng.Sci.66 2660
[47]Walker D M,Tordesillas A 2012 Phys.Rev.E 85 011304
[48]Ghaffari H O Young R P 2012 Europhys.Lett.98 48003
[49]West G B,Brown J H,Enquist B J 1997 Science 276 122
[50]West G B,Brown J H,Enquist B J 1999 Science 284 1677
[51]Garlaschelli D,Caldarelli G,Pietronero L 2003 Nature 423 165
[52]Santillan M 2003 Eur.Phys.J.B 223 249
[53]Duan W Q 2007 Eur.Phys.J.B 59 271
[54]Song D M,Jiang Z Q,Zhou W X 2009 Physica A 388 2450
[55]Ni X H,Jiang Z Q,Zhou W X 2009 Phys.Lett.A 373 3822
[56]Jones D L,Baraniuk R G 1995 IEEE Transactions on Signal Processing 43 2361
[57]Du M,Jin N D,Gao Z K,Wang Z Y,Zhai L S 2012 International Journal of Multiphase Flow 41 91

