电极电压对碳纳米管阴极电离规性能影响的数值模拟*

张虎忠 李得天† 董长昆‡ 成永军 肖玉华

1)(兰州物理研究所真空低温技术与物理重点实验室，兰州 730000)

2)(温州大学微纳结构与光电器件研究所，温州 325000)

(2012年9月26日收到;2013年1月10日收到修改稿)

1 引言

应用碳纳米管(carbon nanotube，CNT)场发射电子技术的电离规是解决极高真空测量难题的有效技术手段[1-3].近十年来，CNT阴极电离规受到了国内外的广泛关注，许多学者先后将CNT阴极应用到不同类型的电离规中，开展了相关的研究工作[4-14]，并针对电极电压与电离规工作性能的相互关系进行了实验研究.Dong和Myneni[4,5]将CNT阴极应用于分离规中，实验研究了阳极电压和门极电压对电子透过率以及阳极电流的影响，测得该电离规灵敏度为0.03 Pa-1，真空测量下限为10-8Pa;Sheng等[6]将CNT阴极应用于鞍场规，研究了阳极电压和灵敏度的相互关系，实验测得该电离规具有较高的灵敏度(1.7 Pa-1)，但是受限于CNT阴极发射电流的稳定性差，其测量下限只达到3×10-5Pa;Huang[8]，Suto[9]，Knapp[12]，Liu 等[14]先后将 CNT阴极应用到B-A规中，实验研究了电极电压对电离规的性能影响，其中，Huang、Liu等针对门极处电子透过率与电极电压的相互关系进行了研究，该规型的CNT阴极电离规所能达到的最大灵敏度为0.15 Pa-1，测量下限最低为10-7Pa[12].综合分析国内外研究结果表明，目前CNT阴极电离规普遍存在灵敏度低和测量下限不能满足应用要求等问题，而研究电极电压和规管结构对CNT阴极电离规性能的影响，是解决以上问题、提高CNT阴极电离规性能的关键因素.

目前针对电极电压对CNT阴极电离规性能影响的分析主要采用实验研究手段，应用数值模拟研究的方法很少;而对于实验研究中采用的各种规型而言，只有分离规能够很好地抑制软X射线效应(电子撞击电极时产生软X射线，软X光子照射离子收集极，发生光电子发射，产生正离子流，导致收集极接收气相离子流时存在本底干扰)和电子激励脱附(ESD)效应(当电子收集极表面吸附一层化学活性气体 (如 O2，H2，H2O，CO 等)时，受到电子碰撞，解吸出正离子和中性分子等，造成电离规的测量误差)[3]，因而基于分离规结构的CNT阴极电离规也是目前为止实现测量下限最低的规型[4].因此，本文基于IE514分离规结构，建立CNT阴极电离规计算模型，采用离子光学模拟软件SIMION 8.0[15]和自编程序，通过计算电离规中的电场分布和电子、离子运动轨迹，研究了电极电压对灵敏度影响;通过分析门极处电子透过率(transmission ratio)和电离规中电子逃逸率(escaped ratio)，研究了电极电压对阳极电流与阴极发射电流比值(Igrid/Ie)的影响.

2 计算模型与分析方法

基于IE514分离规结构的CNT阴极电离规为轴对称结构，其电极结构主要包括CNT阴极、门极、阳极、外屏、反射极和收集极，其三维结构模型和电极相对位置如图1所示.CNT阴极是直径5 mm的圆盘结构，对应门极栅网直径5 mm，透明度67%，阳极栅网直径3 mm，收集孔直径2.5 mm，外屏直径35 mm，门极与阴极间距150µm，阳极栅网顶部距离门极栅网表面4 mm，阳极栅网底部距离收集孔2 mm.

2.1 基本方程和原理

CNT阴极电离规的工作主要受限于灵敏度低、发射电流小、真空测量下限不满足要求、阴极稳定性差等问题.本文主要考虑电极电压对规管中电场分布、灵敏度和阳极电流(阴极发射出来后穿过门极并参与气体分子电离的电子流)与阴极发射电流比值(Igrid/Ie)的影响.

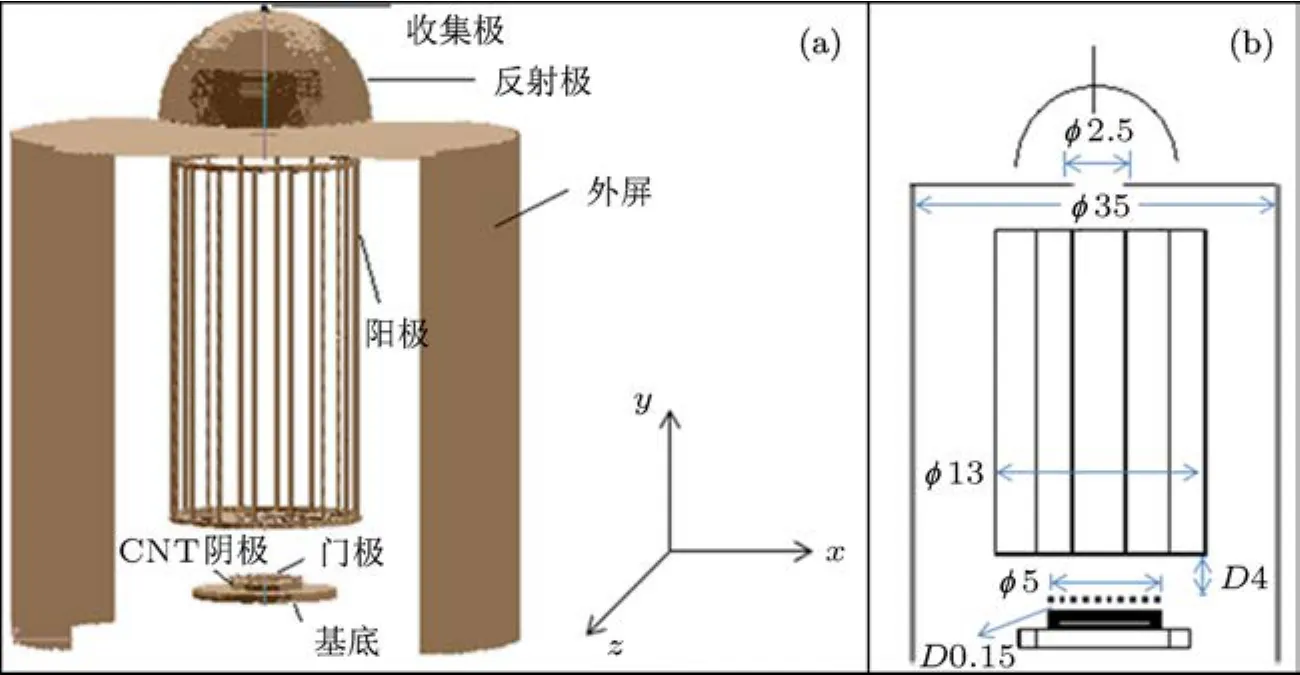
图1 (a)CNT阴极电离规三维物理模型(剖面图);(b)电极相对位置示意图

根据电离规工作原理，其对气体压力的测量和标定是通过探测微电流信号来实现的，具体表达式为

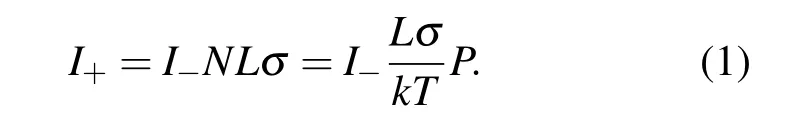
电离规标准方程：

结合(1)和(2)式，推导得出电离规灵敏度定义式如下：

在 (1)，(2)，(3)式中，P 表示环境被测压力，L 表示电子运动轨迹长度，k是波尔兹曼常数，T表示绝对温度，I+是收集极接收的气相离子流，I是电子流，σ表示电子对某种气体的电离横截面，其值正比于气体分子碰撞横截面和电离概率的乘积，碰撞横截面取决于分子平均自由程.

因此，由以上式子可以推导出两种规型灵敏度比对公式如下：

其中，1，2分别代表两种电离规规型，γ表示电离概率.

通常，电离规的阳极电流和灵敏度均由实验测得，在数值模拟中，根据(4)式，灵敏度的理论值可根据电子运动轨迹L和电离概率比对获得.关于电离概率和电子能量之间的关系，Lotz对电子与原子碰撞电离开展了实验研究，并根据电离横截面的实验数据拟合得出近似的经验公式[16]：

其中，σ表示电离横截面;E表示电子能量(eV);χ1表示原子最外层电子电离能(eV);χ2表示仅次于最外层电子的亚层电子电离能(eV)，依次类推;表示加权平均电离能(eV);a=4.0×10-14;ξ≥0.5，作为慢变化函数，其值逐渐趋近于等效电子数.一般情况下，N设置为2，对于Kr，Xe等，设置N=3.国内外学者实验研究的结果与以上经验公式一致性都非常好，因而电离概率的比对将依据已有实验数据进行计算[17].

由于CNT阴极电离规通常工作在超高/极高真空环境下，所以在计算中可将空间电荷效应忽略，对于电离规中电场分布可通过求解拉普拉斯方程(7)获得，电子运动轨迹可通过求解静电场力作用下的牛顿运动方程(8)得到，具体表达式如下：

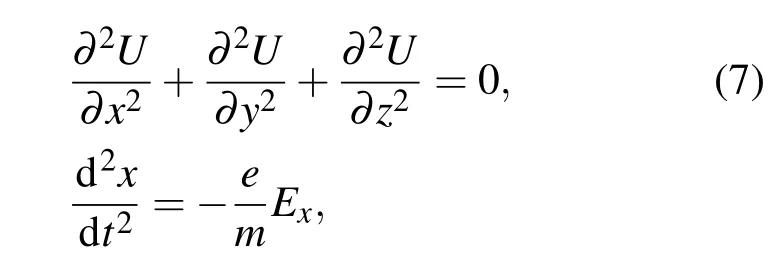
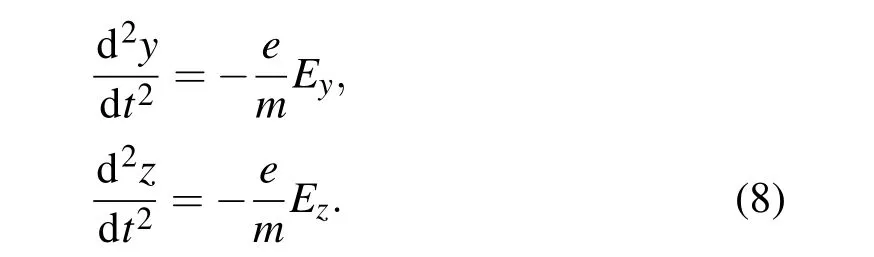
为提高计算精度和模拟结果的正确可靠，在模拟计算中采用三维结构模型，整个CNT阴极电离规计算模型的网格单元均为“六面体”型，总网格数为108个左右.图2给出了CNT阴极电离规电子发射系统(阴极和门极)的网格模型图.根据方程(7)，(8)及相应的边界条件，利用有限差分法和超松弛迭代算法可计算出电离规中的电场分布，采用四阶龙格库塔法计算静电场中的离子和电子的运动方程，最终得到计算模型中离子和电子运动轨迹，用以分析电极电压对CNT阴极电离规电场分布、灵敏度及Igrid/Ie比值的影响.

图2 CNT阴极电子发射系统网格划分图

2.2 边界条件设置

图1对模型的各个边界面都进行了标注，并在表1中做了具体说明.

表1 CNT阴极电离规的边界条件说明

对于传统的分离规而言，其阴极电子发射机制为热致发射，因此在较低的电极电压下即可实现工作.然而，对于分离规结构的CNT阴极电离规而言，其阴极电子发射机制为场致发射(开启电场强度不低于106V/m)，同时考虑到目前CNT阴极的制备和加工工艺水平，需要在较高的电极电压下才能实现工作[18].以门极间距100µm为例，对尺寸5 mm的CNT阴极，针对电离规工作电流满足于0.1 mA的应用要求，门极电压一般在400 V以上，而热阴极一般工作在数十伏电位.因而，高的门极电压对场发射阴极电离规性能的影响是数值模拟研究的重点，电极电压具体参数设置见表2.

2.3 模拟思路和步骤

极高真空测量中，要尽可能延伸CNT阴极电离规测量下限，需要提高灵敏度S和阳极电流Igrid.灵敏度由电极电压和电子有效运动轨迹决定;阳极电流表示参与阳极区域气体电离的电子流，CNT阴极电离规不同于传统热阴极电离规，CNT阴极表面存在一个高电压门极，阴极发射电子不能全部通过门极栅网参与阳极区域气体分子的有效电离，同时又因为门极电压较高(通常达到400 V以上)，参与了阳极区域气体电离的电子中部分会逃逸进入真空环境中，不能全部被阳极接收，因而，CNT阴极电离规阳极电流计算必须考虑门极处电子透过率和规管中电子逃逸率.

表2 CNT阴极电离规电极电压设置

根据2.1中的电离规基本方程，考虑灵敏度定义式(3)和比对计算公式(4)，综合考虑电场分布对电子运动轨迹、门极处电子透过率和电子逃逸率的影响，研究电极电压对灵敏度和Igrid/Ie比值的影响.具体步骤如下：

1)根据当前CNT阴极的物理特性和制备工艺水平，选定阴极的特性参数.

2)基于IE514分离规设定规管结构参数，和选定的CNT阴极相结合，利用离子光学软件SIMION 8.0建立物理模型.

3)确定规管中的有效电离空间.所谓的有效电离空间，是指在该空间中碰撞电离的离子能够被收集极接收.在规管中假设某一点碰撞产生离子的位置，计算该点的离子是否被离子收集极接收，逐次变换碰撞电离产生离子的位置，最终求解得到有效电离空间.

4)变换电极电压设置，计算电子有效运动轨迹(分布在有效电离空间中的电子运动轨迹)，分析相应的灵敏度变化;计算阴极发射电子在门极处透过率和规管中电子逃逸率，分析Igrid/Ie比值.

3 数值模拟与结果讨论

CNT阴极电离规灵敏度取决于规型结构和电极电压，Igrid/Ie比值取决于门极处的阴极发射电子的透过率和规管中电子逃逸率.根据2.1的基本方程和2.3的模拟思路，分析规管中电场分布和有效电离空间，计算电子有效运动轨迹，研究电极电压对灵敏度及Igrid/Ie比值的影响.

模拟中，CNT阴极表面场发射电子相关参数设置如下：电子初始能量为0.1 eV，带一个单位负电荷，质量为5.48579903×10-4amu.电子在Y方向初始位置坐标为4.2 mm，随机分布在XZ平面上直径5 mm的圆面内，圆心坐标为(0，4.2，0).

3.1 电极电压对灵敏度影响分析

电极电压的变化对CNT阴极电离规规管空间的电场分布具有明显的影响，从而会造成有效电离空间和电子有效运动轨迹的变化.图3所示是选择不同电极电压，对应规管中轴线电势分布变化曲线;图4所示即电子总运动轨迹和电子有效运动轨迹的变化曲线.由图可知，电极电压改变造成了电场分布的变化，而且随着阳极电压的升高，电子总运动轨迹不断延长，同等阳极电压条件下，低门极电压(350 V)对应的轨迹最长，有效运动轨迹则呈现出不同特点，当阳极电压为门极电压的1.6倍左右时，有效运动轨迹长度会达到一个局部小峰值.

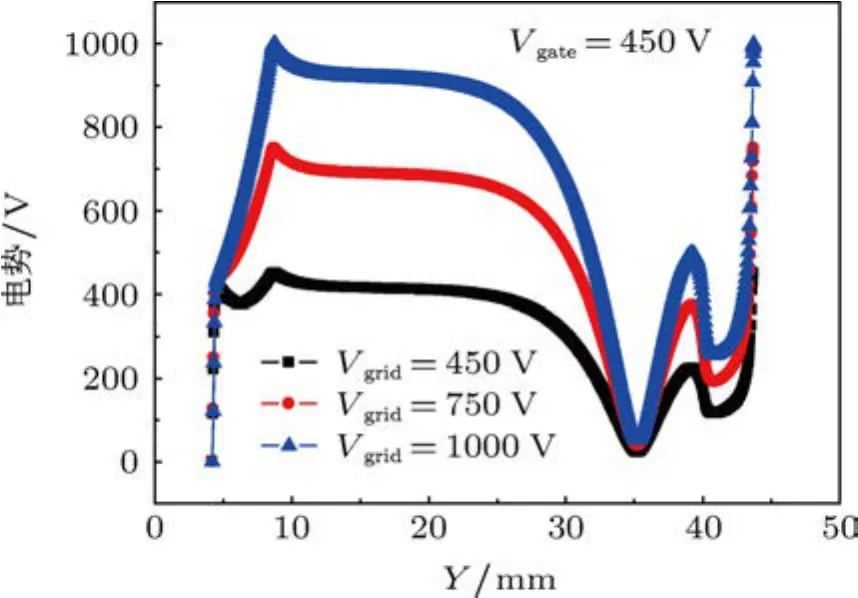
图3 规管中沿Y轴线电势变化关系

图4 电子运动轨迹长度随阳极电压变化关系

对于灵敏度的计算，由定义式计算其数值非常困难，通常利用实验手段获得其实验值，本文通过CNT阴极电离规和IE514分离规的有效电子运动轨迹(分布于有效电离空间中的电子运动轨迹)比对，同时，根据比对公式(3)，考虑了不同阳极电压对应电离概率之间的比对值(以N2分子为例，γ220V/γ500V≈1.6)[17]，最终理论推导得出不同电极电压条件下的CNT阴极电离规灵敏度数值.IE514分离规的电子运动轨迹如图5(b)所示，图5(a)和图6是CNT阴极电离规电子运动轨迹和通过离子运动轨迹模拟获得的有效电离空间(电压设置：门极450 V，阳极700 V，反射极700 V)，与已报道的研究结果符合性很好[4,5].

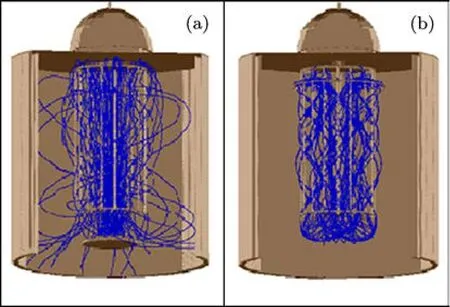
图5 电子运动轨迹 (a)CNT阴极电离规;(b)IE514分离规

图6 有效电离空间二维平面图

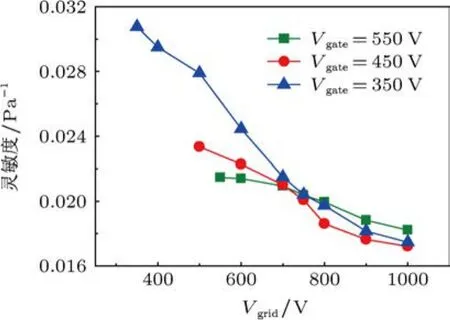
图7 灵敏度随阳极电压变化关系

灵敏度的数值模拟中，根据CNT阴极的工作特性，门极电压分别设置为550 V，450 V，350 V，阳极电压由350 V到1000 V可调，结果如图7所示.当门极电压固定为450 V，阳极电压不断变化时，灵敏度模拟结果介于0.017 Pa-1—0.025 Pa-1之间，其中，阳极电压700V时对应的灵敏度为0.020 Pa-1，此结果与文献报道结果具有很好的一致性.文献[4]的实验研究结果为：0.015—0.019 Pa-1(真空度低于1×10-7Pa)，最高值可以达到0.03 Pa-1.以上分析说明了本文计算模型和模拟方法的正确性，此数值模拟结果也为实验分析结果提供了很好的理论依据.

由图7可知，在三组不同门极电压条件下，灵敏度都会随着阳极电压的升高会逐渐下降，分析其原因，此变化规律是由电子碰撞电离概率和有效运动轨迹决定的.首先，由图4可知，随着阳极电压的升高，电子总运动轨迹会不断延长，而当阳极电压为门极电压的1.6倍左右时，有效运动轨迹长度会达到一个局部小峰值，但是有效轨迹长度随阳极电压变化整体趋于平稳;其次，CNT阴极电离规与传统热阴极电离规(150 V—200 V左右阳极电压)相比，CNT阴极电离规需要在较高的门极电压和阳极电压下工作，而阳极电压升高会造成电离概率的显著下降.以N2分子为例，实验得出电离区域中的电子能量为100 eV左右时，与电离概率相关的系数ε达到最大，其值为10.25左右，随着电子能量进一步增大，ε显著下降，电子能量为500 eV时，ε降为5.53[17].由此可知，阳极电压变化造成的电子有效运动轨迹长度变化一定程度上会影响灵敏度数值，但不是主要影响因素，而导致灵敏度变化的主要原因是门极电压和阳极电压升高所造成的电子电离概率下降.通过对图7中的三条曲线分析表明，选择较高门极电压，对应灵敏度平均值较低，这一结果进一步证明阳极电压的升高造成规管中电子电离概率下降是导致灵敏度下降的根本原因.

3.2 电极电压对电子透过率和逃逸率影响分析

电极电压的变化对CNT阴极和门极之间电场分布会产生较为显著的影响.图8所示是选择不同电极电压，对应阴极和门极之间电势沿X轴方向的分布变化曲线.CNT阴极表面和门极之间的电场作用是实现电子发射，当阴极和门极电压恒定时，阴极电子发射受到的影响很小;而阳极和门极之间的电势差主要影响阴极场发射电子从门极的引出效率——电子透过率(穿过门极栅网进入阳极电离区域的电子流占阴极发射总电流的比例).数值模拟中，在阴极表面设置2000个电子，统计能够穿过门极栅网的电子数，计算透过门极电子数与阴极发射总电子数比值，即电子透过率.模拟结果如图9所示，三组不同门极电压下，电子透过率随阳极电压改变显示出相同的变化趋势，即随着阳极电压和门极电压比值(Vgrid/Vgate)的升高，电子透过率会逐渐增大，因而阳极电压的升高，会获得较高的阳极电流，使得更高比例的阴极发射电子参与气体分子电离.

图8 门极表面沿X轴线方向电势变化曲线

然而实际中，进入阳极电离区域参与气体电离的电子并不能全部被阳极收集，部分电子会被其他电极接收而形成逃逸电子，此部分逃逸电子占透过门极的总电子数的比例定义为电子逃逸率.电子逃逸一方面缩短了电子有效运动路径，使灵敏度降低;另一方面，电子逃逸率的波动会造成灵敏度稳定性变差.电子逃逸率的计算方法类似于电子透过率，即统计逃逸入真空环境中的电子数，并计算其与透过门极总电子数的比值.计算结果如图10所示，电子逃逸率会随着阳极电压的升高而升高.因此，在综合考虑阴极发射电子在门极处电子透过率和规管中电子逃逸率的条件下，模拟真实可测的阳极电流和发射电流比值(Igrid/Ie)变化如图11所示，此模拟结果能够很好地说明已报道实验结果[4,8,14].由此也可见，数值模拟中若考虑了电子逃逸率，使得模拟结果能够与实际实验结果更加一致.

图9 门栅电子透过率随Vgrid/Vgate变化曲线

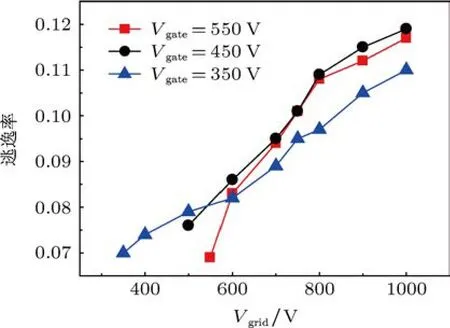
图10 规管中电子逃逸率随阳极电压变化曲线

图11 Igrid/Ie比值随阳极电压变化曲线

4 结论

本文利用SIMION 8.0建立了CNT阴极电离规的物理模型，分析研究了电极电压对灵敏度和阳极电流的影响.由于CNT阴极需要较高引出电场实现电子场发射，所以CNT阴极电离规需要较高的电极电压.结果表明，当阳极电压升高时，Igrid/Ie比值随之增大，但是，对应的电离规灵敏度会随着阳极电压升高而降低.因此，在理论设计和实验研究中，综合考虑电极电压对灵敏度和阳极电流的影响，对于提高CNT阴极电离规的综合性能非常重要.该模拟计算结果与相关文献资料已报道实验结果具有很好的符合性，说明计算模型和参数设置合理，计算结果正确可靠，为实验研究提供了重要的理论依据，对基于分离规结构的CNT阴极电离规的优化设计具有重要的指导意义，也是对国内外普遍采用的实验研究方法[4-14]的一个必要理论补充和验证，推进了对CNT阴极电离规原理特性的理论探索.

此外，通过分析本文所采用的电极电压对CNT阴极电离规性能影响的数值模拟思路可知，该方法将可推广应用于新型CNT阴极极高真空电离规的研发和理论分析中，为解决极高真空测量难题提供了有效的研究途径，具有重要的理论意义和广泛的应用价值.

[1]St.Wilfert，Chr.Edelmann 2012 Vacuum 86 556

[2]Cai M，Li D T，Cheng Y J，Chang P 2011 J.Vac.Sci.Technol 31 732(in Chinese)[蔡敏，李得天，成永军，常鹏2011真空科学与技术学报31 732]

[3]Li D T，Cheng Y J，Feng Y，Cai M 2012 Shanghai Measurement and Testing 39 2(in Chinese)[李得天，成永军，冯焱，蔡敏2012上海计量测试39 2]

[4]Dong C K，Myneni G R 2004 Appl.Phys.Lett.84 5443

[5]Dong C K 2003 Ph.D.Dissertation(Virginia：Old Dominion University)

[6]Sheng L M，Liu P，Wei Y，Liu L，Qi J，Fan S S 2005 Diam.&Rela.Mater.14 1695

[7]In-Mook Choi，Sam-Yong Woo 2005 Appl.Phys.Lett.87 173104

[8]Huang J X，Chen J，Deng S Z，Xu N S 2007 J.Vac.Sci.Technol.B 25 651

[9]Alexanderov S Y，Arkhipov A V，Mishin M V，Sominski G G 2007 Surf Interf Anal.39 146

[10]Xiao L，Qian L，Wei Y，Liu L，Fan S S 2008 J.Vac.Sci.Technol.A 26 1

[11]Hirofumi-Suto，Shunjiro Fujii，Kumiko Yoshihara，Kazuhiro Ishida，Yuya Tanaka，Shin-ichi Honda，Mitsuhiro Katayama 2008 Jpn J.Appl Phys.47 2032

[12]Knapp W，Scheleussner D，W¨uest M 2008 J.Phys.：Conf Ser.100 092007

[13]Yang Y C，Qian L，Tang J，Liu L，Fan S S 2008 Appl.Phys.Lett.92 153105

[14]LiuH R，Hitoshi Nakahara，SashiroUemura，YachachiSaito 2009Vaccum 84 713

[15]Dahl D A，SMION 3D Version 8.0.Idaho National Laboratory，P.O.Box 1625，Idaho Falls，ID 83415 2008

[16]Lotz W 1967 Astrophys.J.Suppl.14 207

[17]Tate J T，Smith P T 1932 Phys.Rev.39 270

[18]Yuan X S，Zhang Y，Sun L M，Li X Y，Deng S Z，Xu N S，Yan Y 2012 Acta Phys.Sin.61 21610 1(in Chinese)[袁学松，张宇，孙利民，黎晓云，邓少芝，许宁生，鄢扬2012物理学报61 216101]