弹性微管内气泡的非线性受迫振动*

王成会 程建春

1)(南京大学声学研究所，南京 210093)

2)(陕西师范大学声学研究所，西安 710062)

(2013年1月28日收到;2013年2月18日收到修改稿)

1 引言

随着生物医学超声的发展，超声波在活体生物组织内的动力学行为越来越受关注.超声造影剂微泡注入血管内可提高超声诊断过程中回波强度，为人们提供了一种便捷、经济且损害极小的诊疗手段.高强度超声波作用于微泡还可产生超声空化效应，从而实现利用超声能量进行局部治疗[1-4].许多研究结果表明，好的超声诊断和治疗效果均与超声波作用下气泡的动力学行为有关，超声造影剂微泡在生物体内的非线性振动可使组织损伤加剧[5-8].超声空化引起组织损伤等生物学效应的机理通常基于以下两种假设[3]：一是空化气泡在非线性振荡过程中崩溃形成高温、高压、冲击波等引起局部压力和温度变化，同时还可能形成高速运动的微射流导致血管壁失去原有平衡并形成损坏;二是在驱动声压的负压相气泡长大压迫血管，在管壁形成较大的周向应力(circumferentialstress)扰动从而导致血管损伤[9].因此，血管内气泡的动力学行为的研究对准确预测超声波作用下造影剂微泡或生物体内原有空化核对肌体组织的影响具有重要的现实意义.

气泡在管状结构内的运动和在无边界液体中的运动相比要复杂得多[10].首先气泡运动受到边界约束，极易形成偏离球形的振动[11]，其形状变化的复杂性决定了它的膨胀和崩溃机制与球状气泡动力学相比会更加复杂;其次有界空间内通常声压空间分布具有驻波特征[12]，从而导致气泡各个方向受力不均匀并使得其形状复杂变化的可能性增大，因此发展更适合管状结构内气泡振动的动力学模型是解决此类问题的关键.Leighton等[13]假定气泡位于一端封闭的刚性管底部且充满了整个截面形成柱状气泡，只有气泡-液体一侧端面可以自由移动，发展了一维气泡自由振动理论.若声波作用下的血管可被看成刚性管，气泡在血管内的运动可看成是两侧液柱-气泡耦合振动系统，这种模型最早由Oguz和Prosperetti[14]提出，Sassaroli和Hynynen[15]以此为基础分析了介质黏热阻尼对系统共振响应的影响.众多研究表明，气泡在管状结构内的振动受到管壁材料的弹性特征、气泡本身的初始状态以及驱动外场的影响，其固有频率由于受到刚性管约束而降低且随着管子长度减小而减小[15-17].若外驱动力较大，由于泡内气体物态变化本身具有非线性特征，气泡-液柱耦合振动系统必将出现非线性声响应[18].在超声波的生物应用中以刚性管模型分析微管内气泡的振动只是一种粗略的理论近似，有待于进一步发展考虑了管壁弹性后管内气泡振动动力学模型，Mateynov等[7]已提出计入管壁弹性后气泡的线性共振模型.本文将考虑管壁弹性对气泡体积变化的影响，以气泡-液柱-管壁耦合振动模型为基础研究微管内气泡的非线性振动规律.

2 模型描述

当气泡的初始半径和管尺寸可相比拟时，可将气泡看成是一个无质量可压缩的柱状弹性体.该模型可用于研究气泡处于管状结构(如毛细血管等)内的气泡动力学问题，最早由Oguz和Prosperetti[14]提出，Martynov等[7]还将此模型推广到二维振动研究气泡与弹性血管之间的相互作用.医用超声造影剂微泡典型半径范围通常在1—5µm之间[15]，和肠系膜等组织结构中毛细血管直径差不多，因此当微泡进入毛细血管后，可近似认为其保持原有初始体积不变但形状变成了截面积和毛细血管相同的圆柱体从而将毛细血管内的液体分为两个液柱，在外场的作用下，液柱、柱状气泡和血管壁体系形成一个耦合振荡系统，如图1所示.

图1 管内柱状气泡振动示意图

式中XB(t)是代表气泡振动的无量纲参数.气泡内气体体积变化源于其轴向和径向尺寸变化的共同作用，因此，泡内气体压力pB(t)可表示为

式中p0为液体静压力，Φ为常数，可认为是与复频率相关的多方指数[14,16].

基于血管壁本身的弹性特征，可将血管壁简化为由覆在组织上的一薄层内皮细胞组成膜弹性结构，其动力学方程近似为

式中dυ和dt分别为血管壁和基底组织的有效厚度，ρυ和ρt分别为血管壁和基底组织密度，pa为外界驱动压力幅值，Eυ为血管壁的杨氏模量，ν为泊松比.

忽略液柱-气泡系统平动对系统振动的影响[18]，两侧液柱在轴向受外部驱动力和泡气体压力的作用下振动，其动力学方程可表示为

式中bv是与黏度阻尼系数.综合(3)，(5)和(7)式可得气泡轴向长度变化相关的动力学方程为

从(3)式知，气泡内气体状态变化本身是一个非线性过程，因此，描述气泡、液柱和血管壁耦合振动的动力学方程(4)和(7)均为非线性方程.泡内体积变化过程中，由忽略管壁位移的高价小量，泡内气体压力pB(t)近似表示为

因此，约去3阶以上的高阶小量后动力学方程(4)和(7)近似为

3 系统的共振

由于管壁弹性的影响，气泡在外场驱动下的非线性振动将变得更加复杂，下面我们将讨论系统共振频率附近的非线性声响应.忽略系统振动阻尼的影响，其线性共振频率ω0满足特征方程

因此，当驱动外力频率等于(12)式中的(ω0)1或(ω0)2，体系将处于共振状态.然而，当在系统的受迫振动中计入非线性项时，其共振响应将出现重要的新特性.

3.1 非线性振动系统的共振频率

比较(21)和(22)式可以看出，管壁振动和气泡轴向振动中非线性参量对系统共振频率的修正影响并不相同，因此，在非线性环境下，管壁振动和气泡轴向振动不能同时达到共振状态.

3.2 受迫振动振幅变化特征

为了解弹性微管内柱状气泡的振动特征，下面我们将采用逐次逼近法研究此二维振动系统在外场驱动下的非线性声响应.受迫振动方程中充当线性恢复力的因子应是振动位移的奇函数，因此去掉(9)和(10)式中振动位移的偶函数项后的耦合动力学方程为

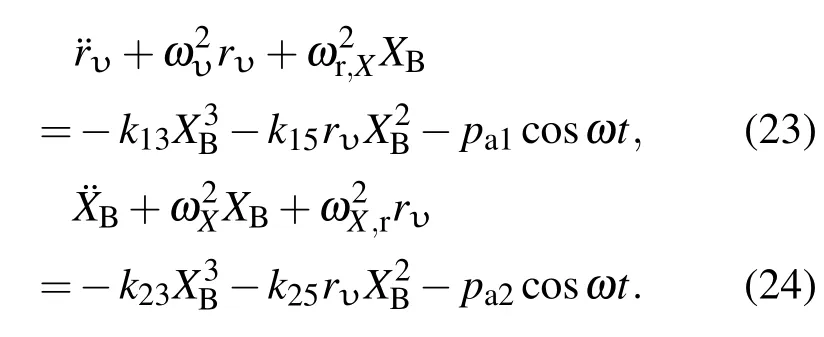
3.3 二分频激励共振响应

振动的非线性除了使系统在基频ω0附近共振现象的性质出现改变外，还导致出现新的共振，即驱动频率显著不同于系统基频ω0的外力可激发频率接近ω0的振动[19].

这个方程组所决定的幅值随频率变化规律和方程组(27)和(28)相同，因此，在液柱-气泡-弹性管壁构成的非线性系统中，利用频率ω0/2的驱动外力也可激发系统在共振频率ω0附近振动，只是强度相对较弱而已.非线性系统的这一重要特性对用超声波激励液柱-气泡-弹性管壁振动系统具有非常重要的意义，因为超声波频率越高，其能量在人体组织中衰减越快[20]，而管壁内气泡共振频率相对较高，为实现超声能量的最佳利用，在实际操作中可采用分频激励的办法，用频率是管壁内气泡共振频率一半的超声波激励气泡振动.

4 数值分析

周围介质为液体时的振动气泡可近似看作球形，其振动状态取决于它的初始半径、液体密度、泡内气体状态、表面张力系数以及环境压力等.对处在弹性管内的气泡而言，气泡两侧液柱的惯性和管壁的刚度都会影响气泡的振动状态.在数值计算过程中，我们首先要确定多方指数Φ，Φ与泡内气体成分有关，同时是气泡初始半径、管半径和驱动声波频率的函数[15,16].Φ的取值取决于泡内气体状态变化.对小气泡或低频情形，泡内气体变化可近似看成是等温过程.当驱动声波频率超过1 MHz或者气泡半径大于4µm，泡内气体的变化通常在等温过程和绝热过程之间.在数值计算过程中各系统变量取值分别为：气泡初始半径RB=3µm，微管平衡半径Rυ=4µm，长度为L=100µm，左侧液柱长度L1=L/5，右侧液柱长度L2=L-L1-LB，管壁厚度dυ=1µm，基底组织厚度dt分别为0和4µm[7];驱动声波压力 pa的有效值分别为1，2和3 atm(1 atm=0.1 MPa);管壁弹性模量分别为0.1，1和10 MPa，泊松比ν=0.5.

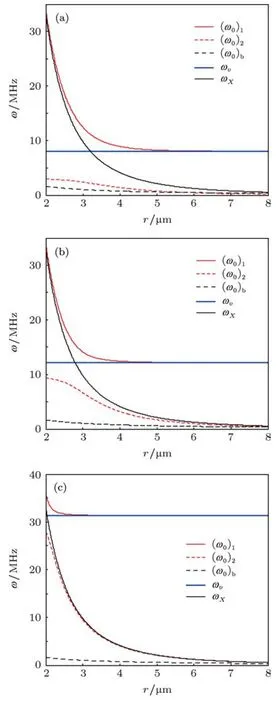
图2 共振频率随气泡初始半径变化(dt=0)(a)Eυ=0.1 MPa;(b)Eυ=1 MPa;(c)Eυ=10 MPa

和柱状气泡的一维纵向振动理论相比[18]，气泡-管壁耦合系统的非线性振动更加复杂，基频振动振幅随驱动外力频率的变化曲线也呈现出新的特征.图3和图4给出了管壁周围基底组织厚度dt=0和dt=4µm时气泡轴向振动基频幅值、管壁振动基频幅值与驱动声波频率间的关系.系统的基频振动幅值-频率响应特性主要表现为：1)出现多个共振响应区，如管壁弹性为1 MPa时，气泡轴向基频振动的共振响应区分别分布在ω/ωX为0.65，0.77和2附近的区域内;随着管壁刚度的减小，低频共振峰对应的频率比越小，即共振峰左移(如图3(1—3)所示);驱动声压幅值不影响共振峰出现的位置，但驱动压力幅值越大，低频响应区内的系统振动幅值越大(如图3(2，4和5)所示).2)振幅具有多值性，因此当气泡受到逐渐变化的频率激励时，振幅不一定是单调增加或减小，还可能出现跳跃现象.跳跃现象通常发生在频率比大于1的声波频率范围内;驱动声波有效压力幅值不同，跳跃现象出现的频率范围也会出现差异，并随着驱动声波压力幅值的增加逐渐向高频区移动(如图3(2，4和5)所示);管壁刚度同样影响频率响应跳跃现象出现的频率范围，随着管壁刚度的增加逐渐向低频区移动(如图3(1—3)所示).3)在同样的激励条件下，出现振幅多值响应的高频区内气泡轴向振动基频幅值大于管壁基频幅值;随着驱动压力幅值增加，高频区内较高分支上的响应幅值几乎不变，而管壁刚度增加不影响高频区内较高分支上的气泡轴向振动响应幅值，但高频区内较高分支上的管壁响应幅值将随着刚度的增加而增加.4)基底组织的存在将抑制管壁在高频区的响应幅值，但却增强了气泡轴向振动响应幅值，因此，基底组织越厚，气泡管壁轴向运动受到的约束越强，气泡越接近一维柱状运动[18].

图3 基频振动幅值与驱动声波频率间的关系(dt=0)

图4 基频振动幅值与驱动声波频率间的关系(dt=4µm)

气泡内气体状态变化的非线性行为成为气泡非线性振动的内因，同时也促使与之耦合运动的弹性管壁作非线性振动.对基频振动而言，其不稳定的非线性响应主要发生在高频区，即在系统线性高频共振频率附近.图3所给出的振动气泡频率响应特征和Martynov等[15]的数值研究结果一致，即在0到∞的驱动声波频率变化区间内存在两个或两个以上的共振响应区，且管壁刚度越小，低频共振频带越窄，振动幅值响应越高.Gao等[9]将管壁看成伪弹性体后研究了不同频率的声波驱动下的管内振动气泡对管壁应力变化的影响，结果表明驱动声波频率越高，管壁的应力响应越弱.管壁的应力响应和管壁形变密切相关，形变越小，应力越小.图3和4给出的系统非线性幅-频关系表明在非共振区，驱动声波频率越高，管壁振动幅值越小，即管壁形变越小，映证了Gao等[9]的研究结论.

图5 三倍频振动幅值与驱动声波频率间的关系(pa=0.1 MPa)

5 结论

Martynov等[15]对弹性管内气泡-液柱耦合振动系统的自由振动特性进行了分析，本文的理论分析是在他们的研究基础上的拓展，主要着眼于外部声场作用下弹性微管内液柱-气泡-管壁耦合振动系统的非线性特征，利用逐级近似法对系统非线性共振频率、基频和三倍频振动幅值响应、分频激励机理等进行了理论分析.通过基频、三倍频振动的幅-频响应的数值分析我们对液柱-气泡-管壁耦合振动特征有了初步的了解，主要表现为：气泡的轴向共振和管壁共振不能同时出现;两垂直方向的振动均表现出幅值响应多值性，进而可能引起系统的不稳定声响应;三倍频振动在低频区响应强于高频区;用频率为系统共振频率一半的声波也可在共振频率附近引起较高的幅值响应.微管内气泡的非线性响应是在外部驱动声压达到一定幅值之后必然引起的动力学结果，因此对微管内气泡的非线性振动分析对研究气泡的动力学行为具有重要的现实意义.

管壁的弹性能否忽略主要取决于它本身的材质和周围介质的约束状态，如许多的生物实验证明当周围组织远大于毛细血管尺寸且组织被加压达到一定程度时，毛细血管几乎可以看作是刚性的[15].尽管如此，在超声波的生物应用中以刚性管模型分析微管内气泡的振动只是一种粗略的理论近似，进一步发展考虑了管壁弹性后管内气泡振动动力学模型，可更准确地描述生物组织血管内气泡受迫振动的非线性特征.

[1]Hu Y T，Qin S P，Hu T，Ferrara K，Jiang Q 2005 Int.J.Nonlin.Mech.40 341

[2]Qin S P，Hu Y T，Jiang Q 2006 IEEE.T.Ultrason.Ferr.53 1322

[3]Freund J B 2008 J.Acoust.Soc.Am.123 2867

[4]Cancelos S，Moraga F J，Lahey R T，Shain W，Parsons R H 2010 J.Acoust.Soc.Am.128 2726

[5]Qin S P，Ferrara K W 2007 Ultrasound Med.Biol.33 1140

[6]MiaoH Y，GracewskiS M，DaleckiD 2009 J.Acoust.Soc.Am.126 2374

[7]Martynov S，Stride E，SaffariN 2009 J.Acoust.Soc.Am.126 2963

[8]SassaroliE，and Hynynen K 2005 Phys.Med.Biol.50 5293

[9]GaoF R，Hu Y T，Hu H P 2007 Int.J.Solids Struct.44 7197

[10]Zhen H R，Dayton P A，Caskey C，ZhaoS K，Qin S P，Ferrara K W 2007 Ultrasound Med.Biol.33 1978

[11]Wang Z Y，Tong A Y 2008 Int.J.Therm.Sci.47 221

[12]Wang C H，Lin S Y 2010 SciChina Phys.Mech.Astron.53 496

[13]Leighton T G，White P R，Marsden M A 1995 Acta.Acust.3 517

[14]Oguz H N，ProsperettiA 1998 J.Acoust.Soc.Am.103 3301

[15]SassaroliE，Hynynen K 2004 J.Acoust.Soc.Am.115 3235

[16]Chen X M，ProsperettiA 1998 J.Acoust.Soc.Am.104 1389

[17]Jang N W，GracewskiS M，Abrahamsen B，ButtaccioT，Halm Robert，DaleckiD 2009 J.Acoust.Soc.Am.126 EL34

[18]Wang C H，Cheng J C.2005 Acta.Phys.Sin.61 194303(in Chinese)[王成会，程建春2012物理学报61 194303]

[19]Landau L D，Lifshitz E M 1976 Mechanics(Third Edition)(London：Pergamon Press)p58

[20]Du G H，Zhu Z M，Gong X F 2001 Fundamentals of Sound(Nanjing：Nanjing University Press)p502(in Chinese)[杜功焕，朱哲民，龚秀芬2001声学基础.(南京：南京大学出版社)第502页]