利用拓扑优化的结构微小损伤定位研究

茅志颖，陈国平，张保强

(南京航空航天大学 航空宇航学院，南京 210016)

结构在使用过程中，由于受外部环境等的影响容易造成损伤，会影响到结构的力学性能，因此结构的损伤定位成为近年来的一个热点问题。由于容易通过实验获得结构模态参数，因此，以结构振动性能为基础的结构损伤定位方法被广泛使用［1－5］。任何结构都可以被考虑成一个带有刚度、质量和阻尼的振动系统。一旦损伤在结构中出现，结构振动的基本参数会被改变。结构模态参数的变化可以作为早期损伤出现在结构中的信号。基于结构振动性能的损伤定位主要是用结构的模态参数如固有频率，模态阻尼和模态振型等来实现［6－11］。

拓扑优化在结构设计优化领域有着广泛的应用，但是在结构损伤定位上的应用还不多见［12－13］，王云，郝际平［14］研究了金属材料内部微观缺陷在几何方程上的体现。本文中，利用渐进结构优化法结合结构模态参数研究了其在微小损伤结构损伤定位应用上的可行性。这种方法基于拓扑优化的特质，可以在结构整个区域寻找损伤点，具有一定的应用前景。

1 损伤定位的数学模型

渐进结构优化法的原理是通过选取适当的准则来判定结构中每一个单元对结构某特性的重要程度，也可以说是使得结构的某一特性达到某一程度，结构中每一个单元的贡献大小。在本文中，即是指通过判断所有单元对于结构的几阶共振频率和反共振频率的贡献的大小来确定结构中最有可能损伤的区域。

损伤定位的数学模型可以表示为如下形式:

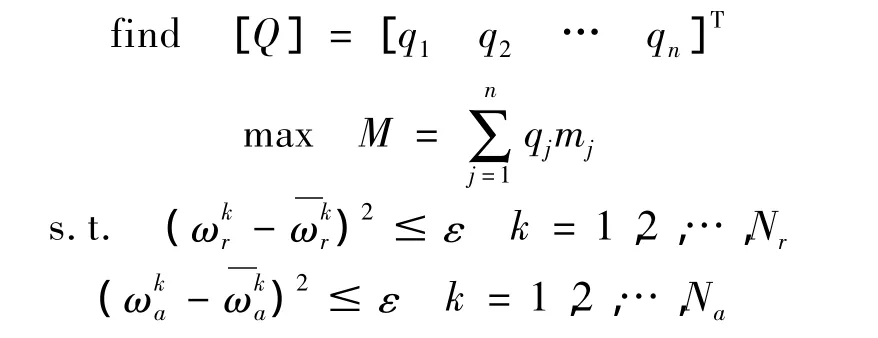
式中Q=［q1q2… qn］T为结构单元拓扑优化设计向量;qi∈{0 1}，分别表示单元在损伤区域和不在损伤区域两种情况;mi为单元i的质量。其中，ωkr和 ωka为原结构的共振频率和反共振频率，和为损伤结构的共振频率和反共振频率，Nr为共振频率的约束个数，Na为反共振频率的约束个数，ε为容许的误差值。

结构振动特性由其特征方程给出，在对结构进行动力学分析时，无阻尼结构的振动特征方程为:

式中:［K］为结构总刚度矩阵，为N阶方阵;［M］为结构总质量矩阵，为N阶方阵;ωi为第i阶固有频率且λi=ω2i;{φi}为第i阶固有振型

经过推导可得结构的i阶频率ωi的灵敏度αij为:

其中［ΔKj］和［ΔMj］为删除第j个单元使结构的质量和刚度矩阵的变化。

对于一般的无阻尼结构，其系统的频响函数矩阵为:

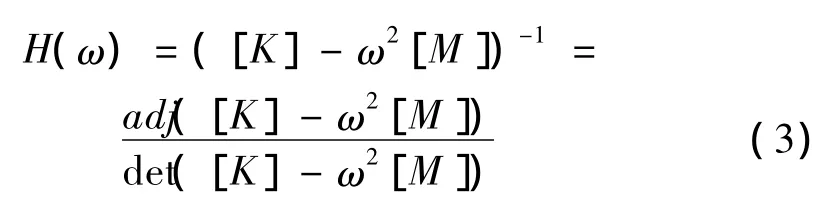
Hts(ω)表示在s自由度激励，在t自由度测量所获得的频响。其中，Hits(ω)的分子是伴随矩阵 adj(［K］－ω2［M］)的第 ts项 H*its(ω)，表示如下:

其中，［Kt，s］和［Mt，s］分别表示删除第 t行和第 s列元素后的质量矩阵和刚度矩阵。当t=s时，称为原点频响函数，当t≠s时，称为跨点频响函数。

结构的反共振频率可以通过下式的特征值问题获得:

其中，λa即为反共振频率所对应的特征值。

当Hts(ω)为原点频响函数时，共振频率和反共振频率交叉成对出现，比结构固有频率少一个，相当于将原系统第i个自由度固定获得的新结构系统的固有频率。而当Hts(ω)为跨点频响函数时，不存在共振频率和反共振频率交叉的特性。结构各原点频响函数的反共振频率一般是不相同的，如图1所示。共振现象是系统的全局现象，而反共振现象是系统的一种局部现象。

对于原点反共振频率，结构中删除单元的特征值变化可以表示为:

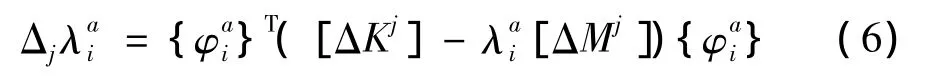
反共振频率特征值λai的变化值为Δjλai。

对于跨点反共振频率，结构中删除单元的特征值的变化量可以表示为:

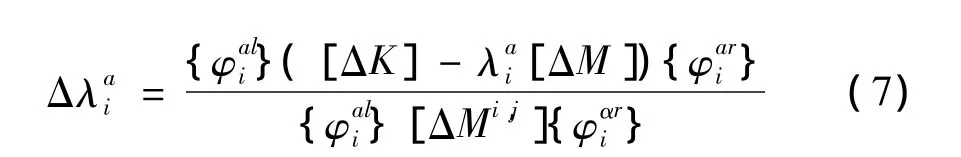
其中，{φail}和{φair}分别为左右特征向量。

由于，原点反共振频率的特殊性，在本文中，所使用的反共振频率都是指某点的原点反共振频率。

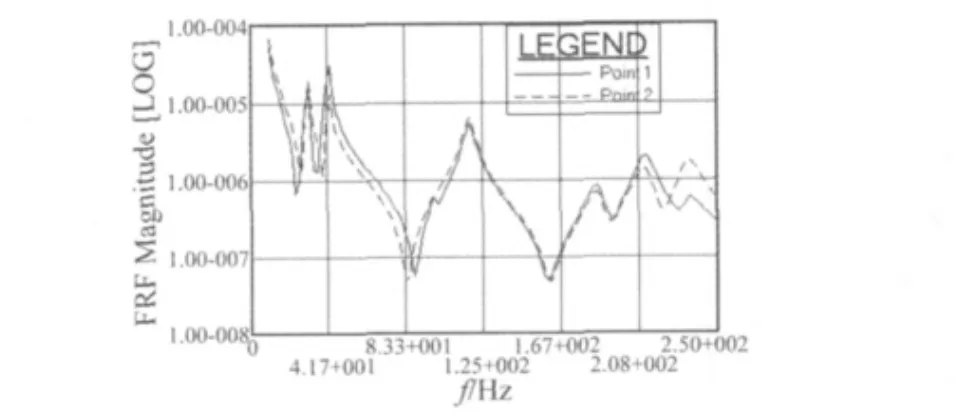
图1 不同点的原点频响函数Fig.1 The P-FRFs of different measurement points

2 基于渐进结构优化法的损伤定位策略

当损伤很小时，搜寻的过程会比较困难。在拓扑优化的过程中，因为设计范围是结构所有的有限元单元，所以当单元数目较多时，寻找微小的损伤单元就会需要很多的工作量。因此在本文中，寻找微小的损伤单元时，采用一种判断方法来逐步排除不可能的单元，同时向损伤区域逼近。这种方法可以直观的表示为如图2所示。

结构的单元是否处于损伤区域的单元，是一个有可能是或者有可能非的模糊概念，因此，结合模糊数学，给每一个单元一个可能是或者可能非的程度大小一个数值衡量。在本文中采用线性隶属函数的中间型表示结构中每一个单元对于结构共振频率和反共振频率变化的灵敏度。

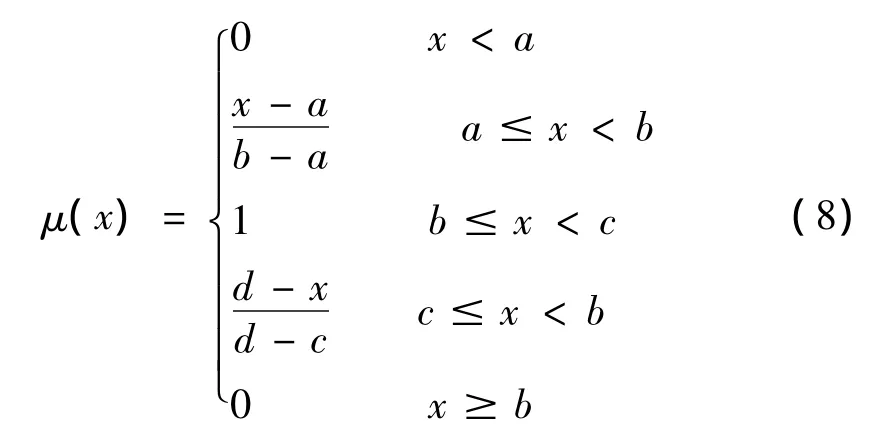
其中，a，b，c，d的计算公式可以表示如下:

图2 损伤区域逼近Fig.2 The approach strategy of damage region

当结构的损伤比较微小时，也即此时结构的几阶共振频率和反共振频率都没有太大的变化，此时，采用区域逼近方法的搜索过程可以表示为如图3所示。

(1)将无损伤结构划分有限元单元，确定初始搜寻范围内的单元集合Ne;

(2)确定无损伤结构的初始共振频率和某点的原点反共振频率以及损伤结构的共振频率和相同点的原点反共振频率;

(3)计算无损伤结构的单元对于某一频率或反共振频率的灵敏度;

(4)利用式(8)对每个单元的灵敏度求取隶属度uiω;

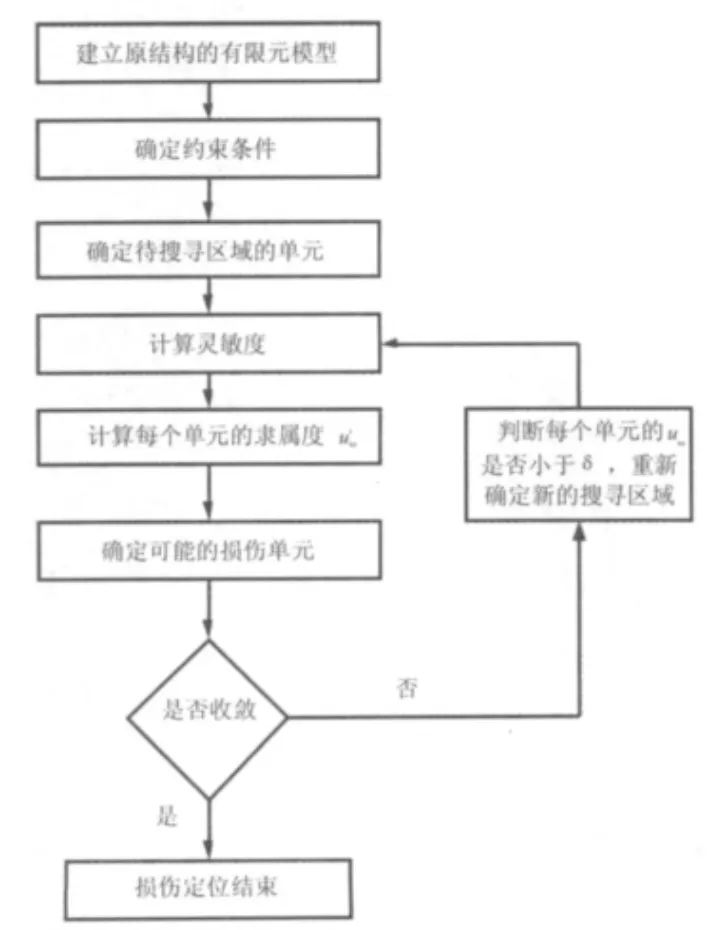
图3 微小损伤定位策略Fig.3 The strategy of tiny damage localization

(5)判断每个单元的 uω是否小于 δ，同时更新Ne;

(6)对Ne的单元，确定可能的损伤单元;

(7)判断是否收敛，如果收敛，则损伤搜寻停止;反之，则重复(3)～(6)步，直到搜寻到最可能的损伤区域。

3 数值算例

算例1，如图4和图5所示分别为一无损伤结构和一微小的凹槽型损伤结构，左端固支。

原结构的共振频率和A点的原点反共振频率以及损伤结构的共振频率和A点的原点反共振频率分别如表1所示。

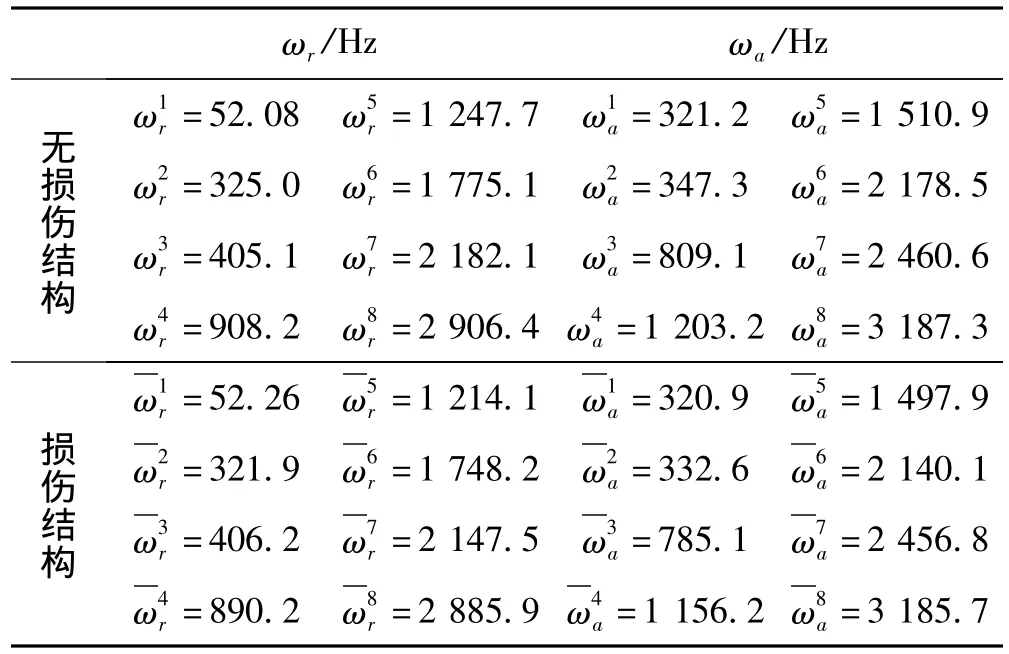
表1 损伤结构和无损伤结构的模态参数Tab.1 Modal data of the undamaged and damaged structure

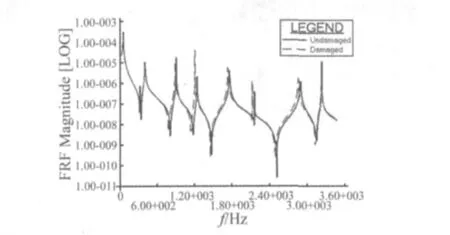
图6 A点的原点频响函数Fig.6 The comparison of the P-FRFs for point A

A点的原点频响函数曲线如图6所示。由图6可以发现，结构的共振频率和反共振频率都发生了较小的变化。取δ值为0.2，结构的损伤定位使用了损伤区域逼近的方法，损伤结构的搜寻过程如图7所示。

图7 损伤定位过程Fig.7 The process of the damage localization

结构的损伤定位过程如图7所示，在搜寻过程中，由于使用了损伤区域逼近方法，随着搜索的进行，其可能得损伤区域在逐步缩小范围，需要判断的单元也在逐渐减小，最后只剩下14个可能的损伤单元。从最后的定位结果看，采用区域逼近的方法，其损伤定位还是比较准确的。

算例2，如图8和图9所示，分别为一无损伤结构和一具有多处微小损伤结构，左端固支。

原结构的共振频率和C、D点的原点反共振频率以及损伤结构的共振频率和C、D点的原点反共振频率分别如表2所示。

图8 无损伤结构Fig.8 Undamaged structure

图9 损伤结构Fig.9 Damaged structure

C点和D点的原点频响函数曲线分别如图10和图11所示。由图10和11可以发现，结构的各阶频率和反共振频率并没有太大的变化，判断是微小损伤，使用损伤区域逼近的方法来搜索损伤区域，取δ值为0.2，其搜寻过程如图12所示。

表2 损伤结构和无损伤结构的模态参数Tab.2 Modal data of the undamaged and damaged structure

图10 C点的原点频响函数Fig.10 The comparison of the P-FRFs for point C

在本算例中，为了识别多处微小损伤，因此，使用了两个点的反共振频率数据，得到的定位结果很准确。相比于算例1只使用了一个点的反共振频率就能获得比较准确的定位结果，在本算例中，当只使用C点的反共振频率时，得到的损伤定位结果如图13所示。

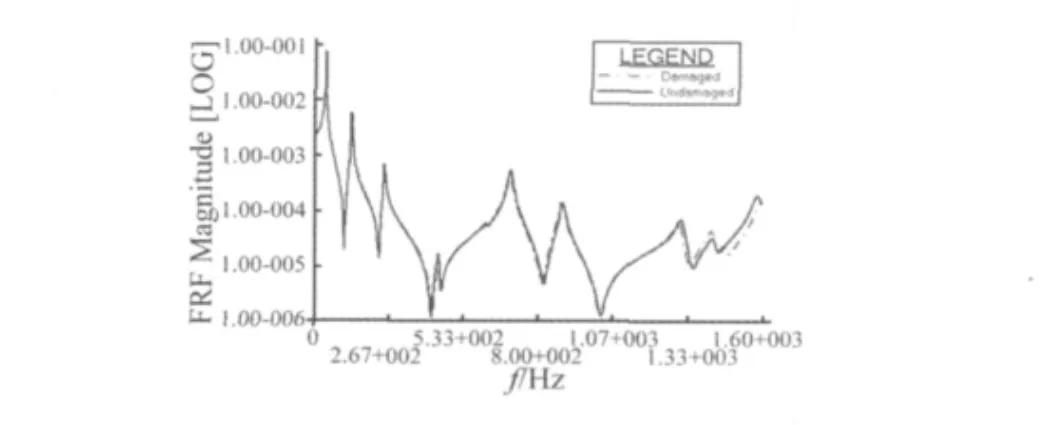
图11 D点的原点频响函数Fig.11 The comparison of the P－ FRFs for point D

图12 损伤定位过程Fig.12 The process of the damage localization

图13所示的是只使用了共振频率和C点一个点的反共振频率的定位结果，从结果看，可以发现，此时得到的定位结果并不是很准确，由此可以说明，为了得到尽可能准确的结果，足够的模态数据，是非常必要的。

图13 没有使用D点反共振频率的定位结果Fig.13 The result without the anti-resonances of the point D

4 结论

本文中以结构模态参数主要是结构共振频率和结构某点的反共振频率为基础，结合渐进结构优化法，讨论了其在微小损伤结构的损伤定位中应用的可行性。文章提出了针对微小损伤结构的损伤区域逼近方法，并提出了合适的结合损伤区域逼近的定位策略。针对本文所提的微小损伤结构，给出了的算例分别对单一的微小损伤和多处微小损伤的结构进行讨论。算例表明，渐进结构优化法在已经测得结构损伤前后共振频率和反共振频率的基础上，在结构整个区域寻找损伤点，即使对于微小的损伤结构也可以有很好的搜寻效果，可以在工程上推广应用。

［1］ Doebling S W，Farrar C R，Prime M B，et al.Damage identification and health monitoring of structural and mechanical systems from changes in their vibration characteristics:a literature review［J］.Technical Report，Research Report LA－13070－MS，Los Alamos National Laboratory，1996.

［2］ Zou Y，Tong L，Steven G P.Vibration-based modeldependentdamagedelamination identification and health monitoring for composite structures-a review［J］.Journal of Sound and Vibration，2000，230(2):357－378.

［3］ Doebling S W，Farrar C R，Prime M B.A summary review of vibration-based damage identification methods［R］.Technical Report，Los Alamos National Laboratory，1998.

［4］ Sohn H，Farrar C，Hemez F，et al.A review of structural health monitoring literature［R］.Technical Report，Report LA-13976-MS，Los Alamos National Laboratory，2001.

［5］ Carden E，Fanning P.Vibration based condition monitoring:a review［J］.Structural Health Monitoring，2004，3(4):355－377.

［6］ Shahdin A，Morlier J，Gourinat Y.Correlating low energy impactdamagewith changesin modalparameters:a preliminary study on composite beams［J］.Structural Health Monitoring，2009，8(6):523－536.

［7］ Shahdin A，Morlier J，Gourinat Y.Significance of low energy impact damage on modal parameters of composite beams by design of experiments［J］.Seventh International Conference on Modern Practice in Stress and Vibration Analysis，MPSVA 2009，2009.

［8］ Tracy J，Pardoen G.Effect of delamination on the natural frequencies of composite laminates［J］.Journal of Composite Materials，1989，23(12):1200－1215.

［9］ Adams R D，Cawley R.The localization of defects in structures from measurements of natural frequencies［J］.Journal of Strain Analysis，1979，14:49－57.

［10］ Richardson M H，Mannan M A.Correlating minute structural faults with changes in modal parameters［J］.Proceedings of SPIE，International Society of Optical Engineering，1993，1923(2):893－898.

［11］ Zhang Z，Hartwig G.Relation of damping and fatigue damage of unidirectional fibre composites［J］.International Journal of Fatigue，2004，24:713－738.

［12］ Lee J S，Kim J E，Kim Y Y.Damage detection by the topology design formulation using modal parameters［J］.International Journal for Numerical Methods in Engineering，2007，69:1480－1498.

［13］ Niemann H，Morlier J，Shahdin A，et al.Damage localization using experimental modal parameters and topology optimization［J］.Mechanical Systems and Signal Processing，2010，24:636－652.

［14］ 王 云，郝际平.含微缺陷金属材料损伤理论的几何拓扑［J］.建筑钢结构进展，2009，11(1):49－53.