高层隔震结构减震机理探讨
商昊江,祁 皑
(福州大学 土木工程学院,福州 350108)
隔震结构的减震机理是延长结构周期,降低地震反应。若对周期较长的高层建筑采用隔震技术,从我国《建筑抗震设计规范》(GB 50011-2010)[1](以下简称《抗震规范》)中可知,长周期部分的地震影响系数曲线下降趋势并不明显,即隔震效果似乎不明显。
然而,高层甚至超高层隔震建筑地震反应时程分析结果表明减震效果显著。日本已建隔震建筑最高为50层、美国为29层。日本一座隔震建筑高94.7 m、场地特征周期为 0.5 s,上部结构自振周期为 1.7 s[2]。
在试验方面,各国研究人员先后进行了十余项隔震结构模型的地震模拟振动台试验。在高层隔震方面,广州大学刘文光 (2002年)与日本研究人员合作,在日本藤田建筑公司振动台上完成了大高宽比(高宽比为5)的5层钢框架的振动台试验和相应的数值模拟[3];哈尔滨工业大学王铁英对一幢三榀二跨的六层框架结构进行了振动台试验(高宽比为 3.1)[4-5];哈尔滨工业大学付伟庆等[6-7]在广州大学抗震中心做了高宽比为5的钢框架振动台试验和相应的数值模拟。以上试验和数值模拟的结果表明了高层隔震结构的减震效果并不比多层隔震结构差很多。
在理论分析方面,对于大高宽比的高层和超高层、塔型隔震结构体系,若采用《抗震规范》中的单质点计算模型便会忽略了上部结构的弯曲以及高阶振型的影响,不能够真实地反映结构的地震反应特性,文献[8]提出用三质点来等效高层隔震结构,并通过高宽比影响系数对模型进行修正,文献[9]从柔度表示的频率方程出发,根据上部结构周期、总基底剪力、顶点位移相等的准则推导出了高层隔震结构的三自由度等效模型。来自这些模型对于高层隔震结构地震反应的分析同样体现了高层隔震结构的良好减震效果。
国内外暂无对高层隔震结构的减震机理进行探讨。与多层结构相比,多振型参与振动是高层建筑的振动特点,本文将从时域和频域两个角度探讨高层隔震结构的多振型减震特性,进一步明确高层隔震结构的减震机理。
为说明高层隔震结构的减震机理,以两项工程为例(A工程为高层,B工程为多层),分别用Etabs有限元分析软件建模,并对比两种结构的减震机理,以此来阐述高层隔震结构的减震机理。
1 工程概况
A工程为我国东南沿海某边防大楼,共24层,钢筋混凝土框架剪力墙结构,底层层高3.3 m,标准层层高3 m,抗震设防烈度为8度,Ⅱ类场地,特征周期为0.4 s。经初步隔震设计,将隔震层设置在基础顶部与一层柱底之间,隔震层层高1.5 m,根据《抗震规范》12.2.3条关于'橡胶隔震支座竖向平均压应力限值'的规定确定隔震支座的选择和布置如下:在边柱和角柱柱下共放置了30个GZY900隔震支座及6个GZP900隔震支座;在剪力墙下每隔1.8 m放置一个GZP350隔震支座,共放置36个;在中柱柱下共放置了39个GZP900隔震支座,隔震层平面简图如图1所示,隔震支座的性能参数见表1和表2。

图1 A工程隔震层平面Fig.1 Isolation layer plane of A project

表1 普通橡胶隔震支座(GZP)性能参数(A工程)Tab.1 Performance parameters of natural rubber bearing(GZP)(A project)

表2 铅芯橡胶隔震支座(GZY)性能参数(A工程)Tab.2 Performance parameters of lead rubber bearing(GZY)(A project)
用Etabs软件对其进行建模,隔震前后各振型周期如表3所示。
B工程为某高校宿舍楼,共7层,钢筋混凝土框架结构,底层3.6 m,其余各层3 m,抗震设防烈度为8度,Ⅱ类场地,特征周期为0.4 s,经初步隔震设计,将隔震层设置在基础顶部与一层柱底之间,隔震层1.5 m,根据《抗震规范》12.2.3条关于'橡胶隔震支座竖向平均压应力限值'的规定确定隔震支座的选择和布置如下:在角柱柱下共放置了4个GZY600隔震支座,在中柱和边柱柱下共放置了40个GZP500隔震支座,隔震层平面简图如图2所示,隔震支座的性能参数见表4和表5。
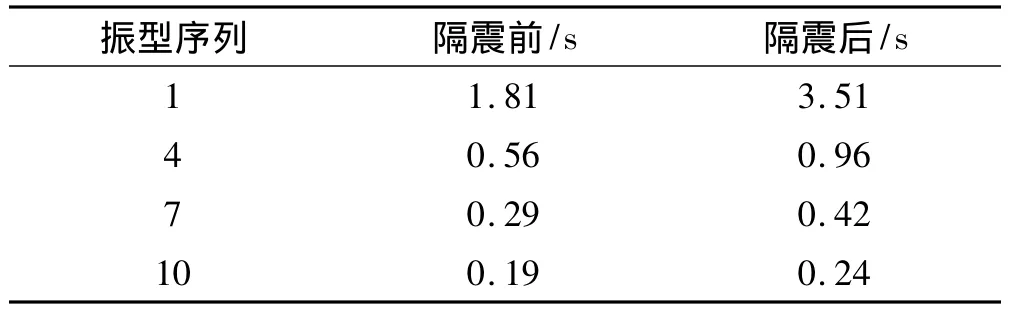
表3 隔震前后各阶振型的周期(X方向)Tab.3 Period of each mode of base-fixed and base-isolated structure(X direction)

图2 B工程隔震层平面Fig.2 Isolation layer plane of B project

表4 普通橡胶隔震支座(GZP)性能参数(B工程)Tab.4 Performance parameters of natural rubber bearing(GZP)(B project)

表5 普通橡胶隔震支座(GZP)性能参数(B工程)Tab.5 Performance parameters of natural rubber bearing(GZP)(B project)
用Etabs软件对其进行建模,隔震前后各振型周期如表6所示,与表3对比发现,高层隔震结构与多层隔震结构第1周期与抗震结构的比分别为1.9和2.6,高层隔震结构不满足周期比2的一般限制[2],若用隔震的最初原理(地震作用随着结构第1周期的增大而减小)判断,地震作用的减少并不明显,因此,这也是需进一步明确高层隔震结构减震机理的原因。

表6 隔震前后各阶振型的周期(X方向)Tab.6 Period of each mode of base-fixed and base-isolated structure(X direction)
2 频域分析
对A工程和B工程分别沿X方向输入Elcentro波、Tarzana波和人工波,峰值调至400 gal(8度罕遇)。
为考察隔震前后结构振动的差异以及减震的效果,经 Etabs软件计算,采用离散 Fourier变换,作出Elcentro波的加速度反应谱和相应的隔震层加速度反应谱(阻尼比ζ=0.05),如图3(A工程)及图4(B工程)所示。

图3 Elcentro波下A工程的地震加速度反应谱和隔震层加速度反应谱Fig.3 Acceleration spectrum of ground wave and isolation layer wave of A project under Elcentro seismic action
从图3和图4中可以看到,在周期较小时,隔震反应谱加速度都减少了很多,而在周期较大时,与地震反应谱差不多,甚至出现了比原来大很多的情况,尤其是多层结构,相对地震反应谱出现了一个很大的波峰(如图4),说明隔震层不仅滤掉了与建筑结构地震反应关系较大的短周期部分的能量,而且把地震动的一部分能量引入了与建筑结构地震反应关系不大的长周期部分,从而大大降低了地震作用。从图3和图4中,我们还可以直观地发现,A工程在短周期部分的反应谱加速度的减少比B工程要多很多,这成为高层的多振型减震的基础。

图4 Elcentro波下B工程的地震加速度反应谱和隔震层加速度反应谱Fig.4 Acceleration spectrum of ground wave and isolation layer wave of B project under Elcentro seismic action
为了解结构各振型的反应谱情况,取Elcentro波下的各阶振型所对应的反应谱数值,如表7和表8所示,从中可以看出:无论是高层隔震还是多层隔震,各阶振型的反应谱加速度都减少了很多,说明无论是高层隔震结构还是多层隔震结构都存在多振型减震的作用,但在高层结构中,高阶振型反应谱加速度的减少量相对于第一阶振型反应谱加速度的减少量要大很多,而在多层结构中,高阶振型的减少量与第一阶振型差不多,这便使得多振型减震在高层结构当中的效应要比多层结构明显。
3 时域分析
为了说明高层隔震结构的减震机理,可以设想:以基底剪力作为研究对象,逐次叠加上高阶振型,若其减震率有较大的提高,则说明高阶振型的减震在多振型减震中的权重不可忽视,也就说明了高层隔震的“多振型减震”机理。

表7 Elcentro波下的A工程各阶振型加速度反应谱Tab.7 Acceleration spectrum of each mode of A project under Elcentro seismic action

表8 Elcentro波下B工程的各阶振型加速度反应谱Tab.8 Acceleration spectrum of each mode of B project under Elcentro seismic action
仍以 A、B两个工程为例,对其输入Elcentro波、Tarzana波和人工波,峰值调至400 gal(8度罕遇)。将隔震层的运动视为一种地震动,并将三种地震波以及在上文的“频域分析”中提取到的三种隔震层时程输入到原抗震结构中,作图5和图6对比其X方向基底最大剪力(包含正负两个方向)减震率。减震率的计算方法是:(原抗震结构基底最大剪力-隔震结构最大剪力)/原抗震结构基底最大剪力×100%。
从图5中可以看出,对于高层隔震结构,随着高阶振型的叠加,无论正向还是负向的基底最大剪力的减震率都有较大的提高,尤其是从前3阶到前6阶较为明显,而后的高阶振型由于振型质量参与系数的下降,减震率的变化不是很明显,而对于多层结构,从图6中可以看出,叠加上高阶振型后,减震率变化不大,且随着高阶振型的叠加,减震率几乎都出现了不同程度的下降。

4 结论
在高层隔震结构中,高阶振型反应谱加速度的减少量相对于第一阶振型反应谱加速度的减少量要大很多,而在多层结构中,高阶振型的减少量与第一阶振型差不多。高层隔震结构与多层隔震结构在减震机理上的差别是:多层隔震结构的高阶振型减震效应很小,且以第一振型减震为主,而高层隔震结构存在较大的高阶振型减震的效应,从而产生了其多振型减震的效应。
[1] GB 50011-2010,建筑抗震设计规范[S],2010.
[2] 日本建筑学会.隔震结构设计[M].刘文光译.北京:地震出版社,2006.
[3] 刘文光,闫维明,霍 达,等.塔型隔震结构多质点体系计算模型及振动台试验研究[J].土木工程学报,2003,36(5):64-70.
[4] 王铁英,王焕定,刘文光,等.大高宽比橡胶垫隔震结构振动台试验研究(1)[J].哈尔滨工业大学学报,2007,(2):2060-2064.
[5] 王铁英,王焕定,刘文光,等.大高宽比橡胶垫隔震结构振动台试验研究(2)[J].哈尔滨工业大学学报,2007,(2):196-200.
[6] 付伟庆,王焕定,刘文光,等.LRB隔震结构模型振动台试验研究(1)[J].哈尔滨工业大学学报,2007,39(2):201-205.
[7] 付伟庆,王焕定,刘文光,等.LRB隔震结构模型振动台试验研究(2)[J].哈尔滨工业大学学报,2007,39(4):521-524.
[8] 刘文光,杨巧荣,周福霖.大高宽比隔震结构地震反应的实用分析方法[J].地震工程与工程振动,2004,(4):116-121.
[9] 付伟庆,王焕定,丁 琳,等.规则型高层隔震结构实用设计方法研究[J].哈尔滨工业大学学报,2007,(10):1542-1545.
[10] 吕西林.高层建筑结构[M].武汉:武汉工业大学出版社,2000.

