基于滚动轴承故障诊断的AR预测滤波器阶数问题研究

从飞云，陈 进，董广明

(上海交通大学 机械系统与振动国家重点实验室，上海 200240)

滚动轴承是应用最为广泛的机械零件之一，同时也是机械设备中最容易损坏的元件之一。据统计，在使用滚动轴承的旋转机械中，大约有30%的机械故障都是由于轴承引起的。因此轴承是我们在进行设备维护与诊断过程当中必须重点关注的部件。近年来，越来越多的学者对轴承信号的分析和处理进行了有效的研究，提出了多种不同的方法和理论，其中大多数方法的核心思想都是集中于特征提取的研究上，即将故障特征信号有效地从原始信号中提取出来。

振动信号分析方法已经被广泛应用到轴承的故障诊断领域。当滚动轴承发生故障时，其振动信号往往表现为一种幅值调制的特性［1］。Dron在利用AR模型对成型压力机进行状态监测与维护研究时指出，参数化方法对于设备的早期故障特别敏感，同时还表示在应用AR模型进行分析时，其模型的阶数确定方法是在应用过程中遇到的最主要问题［2］。

由于在实际的故障诊断过程中，故障信号往往伴随着比较大的背景噪声，甚至有可能出现信号被噪声湮没的情况。本文从AR预测滤波器对信号进行降噪处理的角度出发，详细讨论了此AR模型的阶数选择与信噪比的关系，提出了一种基于最大峭度准则的阶数选择方法。

1 AR模型及应用

1.1 AR模型预测滤波

AR模型在信号处理方面的广泛应用开始于对高分辨率谱估计的需求［3］。他是一种基于有理传递函数的参数化建模方法。由于AR模型的参数包含了系统的重要状态特征且对系统的状态变化非常敏感，将其应用于时间序列的分析具有重要的价值［4］。

当数据序列是沿整个信号序列滑动而得时，就形成信号的自适应AR谱。对于非平稳随机信号，在短数据序列段内可认为是平稳随机的，故可用自适应AR谱分析法来研究［5］。而所谓的时间序列AR模型的参数估计，就是选择合适的参数使得模型的残差εk为白噪声。常用的方法有时序理论法和优化理论估计法，设存在一时间序列xn，则存在一正整数p，使得:

其中Γ表示Wold分解算子，p表示分析阶数，ap表示AR模型参数，关于时间序列xn的AR模型可表示为如下形式:

其中εk是一个白噪声过程，其方差大小表示了AR线性预测滤波器的估计误差［6］。利用AR模型进行线性预测滤波的过程如图1所示，原始信号经过p阶AR线形滤波器进行预测滤波后可得到新的信号Yn，由于在滤波过程中的卷积操作关系，最后还需要对Yn进行截取，得到在信号 Yn－p。

图1 AR预测滤波器的滤波过程Fig.1 The process of AR prediction filtering

1.2 滤波器的阶数选择

AR模型阶数的选择对于故障诊断结果的精确性非常重要，国内外有许多相关文献对于此问题进行过比较深入的研究，图2给出了目前阶数选择问题上主流的一些方法及其分类，而实际应用最广泛的则是其中的信息量准则判别法，主要有 AIC准则［7］、FPE准则［8］、MDL准则和CAT准则。对于p阶AR预测滤波器，为计算各个信息准则，必须首先根据公式(3)得到滤波的预测误差σ2p:

由已知的预测误差σ2p我们可以分别计算得到上述四种准则的评判指标，以对应的定义公式如下所示:

通过上述公式可分别计算得到各个判据的评判指标，当在一定阶数范围内，一般认为以所得最小指标值对应的阶数为其最优阶数。对于不同特征的信号，每个准则的判断准确度也不尽相同，对于一个合理优异的判据来说，其发生“过优”和“欠优”的概率应相对较低［9］。而且，在实际运用中，他们往往都存在如下的不足:

(1)需要大量的数据点数来提高其评判的准确性。

(2)单独使用其中一种判据其可信度往往不高［10］。所需的最优阶数应该是各个算法得出结果的一个综合考虑结果。

由此可知，获取AR模型的最优化阶数是一个复杂且困难的问题，下面我们将讨论在滚动轴承的故障诊断领域中，AR模型的阶数选择问题所需要解决的问题。

图2 最佳阶数p的选择方法Fig.2 Methods for selecting the optimum order p

2 滚动轴承故障诊断的阶数选择

首先我们利用滚动轴承的仿真信号来详细讨论AR预测滤波器的阶数选择和故障信号之间的关系，从而给定可靠的阶数选择方案。根据公式(8)可得到滚动轴承仿真信号。其中A表示故障类型，党委常数时则表示为外圈故障，B表示系统衰减阻尼比，fn表示系统结构振动频率，n(t)为噪声:

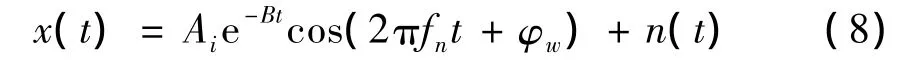
设置系统的采样频率fs为25 600，结构共振频率fn为4 000 Hz，故障频率fm为20 Hz，阻尼比B为300，根据滚动轴承故障原理我们可知，故障信号表现为一系列故障冲击脉冲与其结构共振的调制过程，B表示了故障冲击的衰减速度大小，根据采样频率与共振频率之间的关系，冲击衰减信号(如图3所示)可看成是以B的衰减速度以fn为衰减频率的共振衰减准周期信号，其衰减周期的数据点数为:

即平均6.4个点信号经历一个衰减周期，通过对AR预测滤波器的研究［1，11］，我们提出了衰减信号整周期截取的定阶准则，同时，基于该预测滤波器的消噪考虑，当系统存在背景噪声时，其阶数应当取当周期衰减信号湮没入噪声前最大整周期点数。为了验证本文提出了定阶准则的有效性，根据轴承故障的信号原理，其时域信号的故障严重程度可用峭度指标进行衡量，图4表示了仿真信号加入噪声后信噪比为－15 dB的时域信号，图3(b)表示了不同阶数的滤波器滤波后信号的峭度指标对应图，由图可知，该信号在阶数达到45的时候，峭度取到最大值，此时根据图3(b)中的显示，45点刚好是原始冲击信号进过7个衰减周期的整周期点数，由此可知信号在冲击衰减7个周期后就被噪声湮没。图4(c)给出了利用45阶预测滤波器滤波后得到的信号。

图3 外圈故障仿真信号Fig.3 Simulated signal of outrace transient signal

为了进一步论证阶数选择与信噪比的对应关系，我们给出完全一样的信噪比，但是前述仿真信号的阻尼比由300增至1 000，即其共振衰减速度加快，根据本文提出的阶数准则，噪声能量不变，若衰减速度加快，则意味着冲击衰减将经历更少的衰减周期即被噪声湮没(相对于上述的7个周期)，图5给出了相关的分析结果，由图5(b)可知，19可作为滤波器的最优阶数，再结合图5(c)中的原始冲击局部放大图可得19为衰减周期的3倍，即当原始冲击信号经过三次衰减后即被噪声所湮没。由此分析可知，本文提出的基于整周期截取的AR预测滤波器阶数准则完全适合应用于滚动轴承的故障诊断，同时也揭示了AR预测滤波器应用于滚动轴承信号时其阶数选择与信噪比、衰减速率、采样频率、共振频率之间的详细关系。

3 实验研究

为验证本文所提出的阶数确定方法在实际轴承故障诊断中的应用价值，设计了如下实验。如图6表示了实验设备的安装构成图，此实验在滚动轴承中的测试实验台ZST－1上进行，数据采集卡采用NI6023e，采集软件使用labview编写，采样频率为25 600。

图6 实验设备安装图Fig.6 Installing drawing of experiment

图7(a)显示了采集获得的原始振动信号时域波形，然后我们给出了了不同滤波阶数滤波后的峭度指标与对应阶数之间的关系图，如图7(b)所示，根据此图得到的信息，可知32是比较理想的滤波器阶数，利用此阶数进行AR预测滤波后得到的信号如图7(c)所示，由图可知其降噪效果很好。

图7 实验信号阶数选择及滤波分析结果Fig.7 Order selection and filtering analysis of experimental signal

4 结论

本文通过AR预测滤波器对滚动轴承故障诊断中降噪性能的研究，详细讨论了AR预测滤波器在轴承故障诊断中的阶数选择问题，揭示了其最优阶数选择与轴承的信噪比、衰减阻尼比、采样频率和结构共振频率之间的关系，提出了基于McFadden模型的衰减信号整周期截取准则，同时进一步利用峭度最大化原理给出AR预测滤波器的最优阶数参考。

［1］ McFadden P D，Smith J D.Model for the vibration produced by a single point defect in a rolling element bearing［J］.Journal of Sound and Vibration，1984，96(1):69－82.

［2］ Dron J P，Rasolofondraibe L，Couet C，et al.Fault detection and monitoring of a ball bearing benchtest and a production machine via autoregressive spectrum analysis［J］.Journal of Sound and Vibration，1998，218(3):501－525.

［3］ Marple L.New autoregressive spectrum analysis algorithm［J］.IEEE Transactions on Acoustics，Speech，and Signal Processing，1980，28(4):441－454.

［4］ Cheng J S，Yu D J，Yang Y.A fault diagnosis approach for roller bearings based on EMD method and AR model［J］.Mechanical Systems and Signal Processing，2006，20(2):350－362.

［5］ 张海勇，李 勘.非平稳随机信号的参数模型分析方法［J］.系统工程与电子技术，2003，25(003):386－390.

［6］ 徐 峰，王志芳，王宝圣.AR模型应用于振动信号趋势预测的研究［J］.清华大学学报，1999，39(004):57－59.

［7］ Akaike H.Fitting autoregressive for prediction［J］.Ann.Inst.Math，1969，21:243－247.

［8］ Akaike H.A new look at the statistical model identification［J］.IEEE Trans.Autom.Control，1974，19:716－723.

［9］ Broersen P M T，Wensink H E.On the penalty factor for autoregressive order selection in finite samples［J］.IEEE Transactions on Signal Processing，1996，44(3):748－752.

［10］ Thanagasundram S，Schlindwein F S.Autoregressive order selection for rotating machinery［J］.International Journal of Acoustics and Vibrations，2006，11(3):144－154.

［11］ Endo H，Randall R B.Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter［J］. Mechanical Systems and Signal Processing，2007，21(2):906－919.