滚动汽车轮胎自激振动仿真及其影响因素分析
左曙光,苏 虎,王纪瑞
(同济大学 汽车学院,上海 201804)
自激振动是指振动系统通过本身的运动,不断地向振动系统内馈送能量,完全依靠本身的运动来激励的一种运动形式,与外界激励无关。
国内在自激振动方面的研究主要体现在分析分段光滑非线性自激振动方面,包括重型机床的“爬行”、机床切削的颤振、火车的“蛇行”运动、流固祸联系统的自激振动、飞机的颤振以及具有间隙的系统的自激振动等。龚庆寿[1]指出机床以及液压系统的“爬行”是由摩擦引起的自激振动现象,并对自激振动产生爬行的机理进行了分析,通过建立进给系统运动模型,对爬行现象进行了理论分析,进而得出了摩擦力的变化是产生爬行的原因,并给出了抑制和消除机械系统爬行的解决办法。
国外专家学者对于自激振动的研究主要包括由风所引起的桥的自激振动、干摩擦引起的自激振动、气流压力引起的桅杆的自激振动、石油开采钻井设备的分段非连续自激振动、峰鸣现象等等。其中Keele大学力学系的Mcmilla[2]针对峰鸣现象对干摩擦引起的自激振动进行了分析,指出峰鸣现象是一种自激振动,这种振动是在像车轮、琴弦类的物体当中由于干摩擦驱动力而引起的,其振动机理是很难定义的,并且通过将静摩擦和动摩擦结合在一起的方式提出了一种振动模型,结果表明该模型能较好地解释蜂鸣现象。
在轮胎自激振动方面,日本Sueoka[3]研究小组,将两个相接触的旋转滚轮之间产生自激振动的原理用于研究汽车轮胎周向多边形磨损现象,解释了可能产生周向规则多边形磨损的原因,然而文中却没有考虑悬架形式、车轮侧偏角与外倾角、轮胎与路面相互作用等因素的影响。同济大学汽车学院在此基础[3]上进一步开展研究,通过对自激振动模型的稳定性进行研究,找出了产生规则轮胎多边形磨损的行驶车速范围[4-5]。然而以上研究都忽视了胎面与路面之间动摩擦系数与静摩擦系数相互转化时对自激振动以及多边形磨损的影响,也没有对各参数进行灵敏度分析。因此,本文先对自激振动机理进行阐述,然后结合轮胎三维有限元模型,采用能综合体现动、静态摩擦特性的LuGre摩擦模型,基于大型有限元分析软件MSC.Marc,对轮胎多边形磨损中自激振动的规律以及影响因素进行研究,为有效降低因多边形磨损引起的轮胎报废数量,合理设计和匹配车辆参数提供依据。
1 轮胎自激振动有限元模型
1.1 胎面自激振动机理分析
为分析胎面在侧向上的自激振动,以单自由度振动模型为例,将胎面离散化为若干集中质量块,限制各质量块仅有沿轮胎宽度方向上的线自由度,并且在相邻质量块间存在着弹簧和阻尼的作用。取任一接地质量块作为研究对象,建立胎面-路面单自由度理论模型,如图1所示。
为考虑接地胎面侧向的自激振动现象,将模型中的轮胎假设为静止物体,而将此模型中的路面设为运动的,即在沿着轮胎的宽度方向上路面与轮胎之间存在一定的相对速度。胎面仅有一个侧向平动自由度,与轮胎之间可看作是带阻尼的弹簧连接,弹簧刚度Ks即为轮胎的侧向刚度,阻尼器阻尼Cs即为轮胎的侧向阻尼,接地胎面的质量m由接地印迹面积与胎面的厚度确定。
在汽车前进过程中,由于前束角的存在,轮胎在侧向方向上会获得一定的速度输入。设前束角为θ,将汽车前进速度V分解到侧向上,得到轮胎在侧向上相对于地面的线速度Vb:
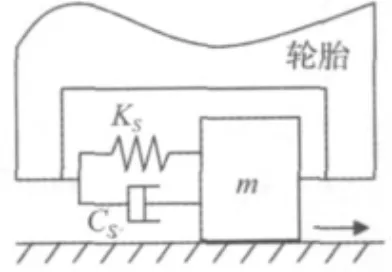
图1 轮胎-路面单自由度模型Fig.1 Model of vibration of single degree of freedom between road surface and tire tread

在模型中,胎面振动能量的输入来源于胎面与地面之间持续不断的摩擦力作用,即两者之间的相对速度变化是激励源。为了便于分析,将轮胎与地面间的平动Vb简化为皮带轮的转动。简化后的模型如图2所示。
设胎面质量块m在皮带上相对于初始位置(即弹簧及阻尼器不受力时的位置)的位移为 s,质量块 m与皮带间的相对速度Vr为:
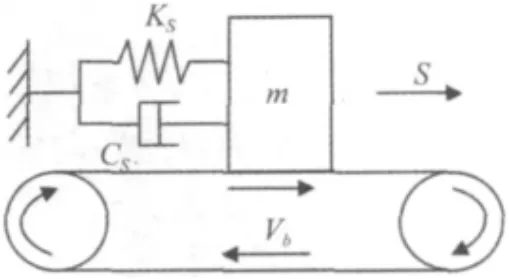
图2 胎面质量块链接简化模型Fig.2 Simplified interlinking model of tire tread mass element with road surface

根据牛顿-欧拉运动学方程,可以列出胎面质量块m侧向振动的动力学方程如下:
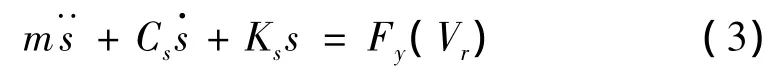
式中Fy(Vr)为胎面所受的侧向力,是由轮胎接地处摩擦力引起的,是物体与皮带轮间相对速度Vr的函数:
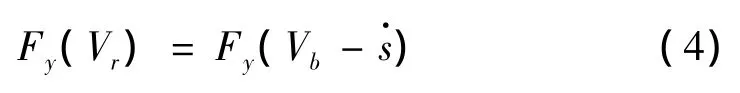
将Fy(Vr)在任意速度Vr处进行一阶泰勒展开,得:
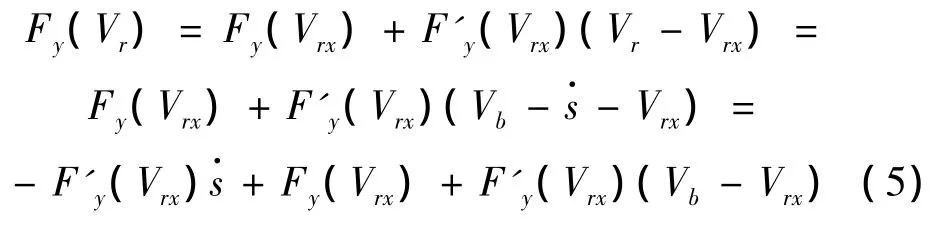
将式(5)代入式(3),略去与振动无关的常数项并整理,得到在物体与皮带轮之间的相对速度Vr=Vrx时的瞬时振动微分方程:
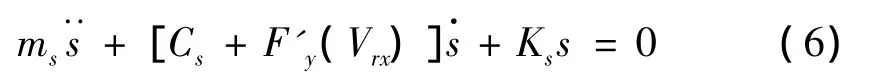
此时,该振动系统的当量阻尼为:
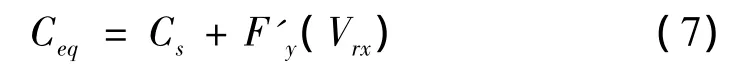
根据Ceq值的不同,对于该系统有如下讨论:
① 正阻尼状态:当Ceq>0时,F'y(Vrx)>-Cs,该振动系统处于正阻尼状态,系统的能量被损耗,振动有衰减趋势;
② 无阻尼状态:当Ceq=0时,F'y(Vrx)=-Cs,该振动系统处于无阻尼状态,系统的总能量不变,维持等幅振动;
③ 当 Ceq<0时,F'y(Vrx)<-Cs,该振动系统处于负阻尼状态,系统从外界吸收能量,振动有增强的趋势。
对于不同的摩擦模型,摩擦力曲线在Vr=Vrx处的斜率F'y(Vrx)并不相同,尤其在摩擦模型曲线的“负斜率”特性阶段,此时F'y(Vrx)为负值。因此,若阻尼器的阻尼Cs很小,轮胎-路面干摩擦振动系统的当量阻尼Ceq会随着相对滑动速度Vr的变化而在正值和负值之间不断变换,使得该振动系统时而吸收能量时而消耗能量,呈现动态平衡,维持稳定的等幅振动,即形成自激振动。
对于干摩擦振动系统来说,摩擦特征曲线中的负斜率部分是形成自激振动的根本原因。若此负斜率部分足以抵消振动系统自身的正阻尼,则该振动系统便会表现出整体负阻尼状态,进而产生自激振动;而若摩擦特征曲线的负斜率特征不明显,或者振动系统自身的正阻尼比较大,则该振动系统无法出现整体负阻尼状态,振动将被衰减,因此无法形成自激振动。为此本文将根据理论分析模型,考虑轮胎三维特性,结合LuGre摩擦模型,利用有限元方法对轮胎胎面自激振动现象进行研究。
1.2 轮胎三维有限元模型
正确建立轮胎的三维模型是进行高速滚动轮胎自激振动仿真的关键,考虑橡胶的非线性、帘线与橡胶复合材料的各向异性、轮胎大变形导致的非线性边界条件以及滚动惯性对轮胎滚动特性的影响,建立了三维子午线轮胎非线性有限元模型。如图3所示,子午线轮胎由胎面、胎侧、胎肩、帘布层、带束层和胎缘组成。本文的建模思路是先生成轮胎截面的二维结构,再应用MSC.Marc提供的3D轴对称扩展作业功能实现二维单元的轴对称三维扩展,最终生成如图4所示的三维轮胎实体模型[6]。
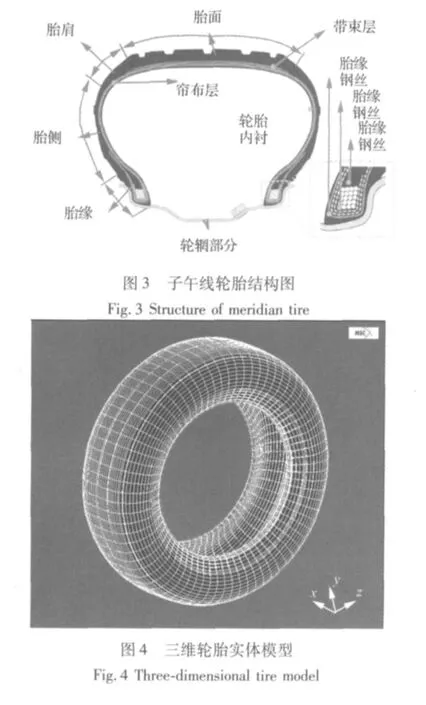
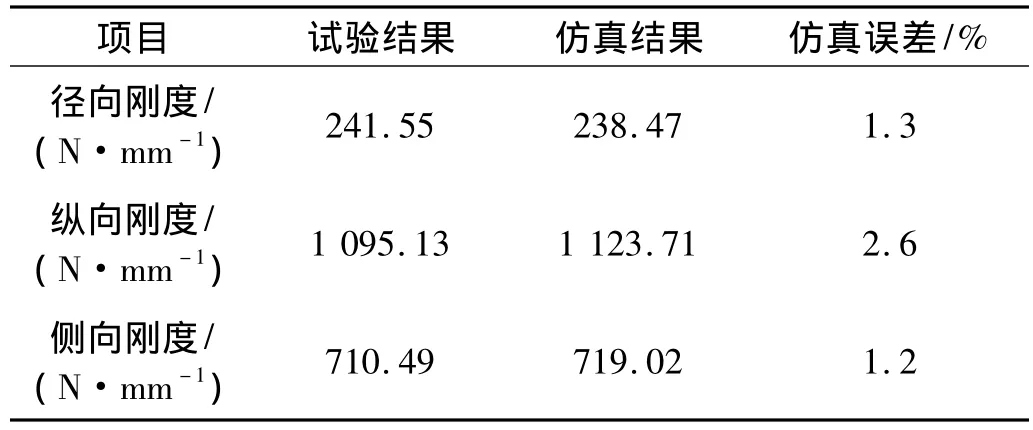
表1 轮胎三向刚度仿真与试验结果比较表Tab.1 Comparison between experimental results and simulation data on tire stiffness in three directions
在对轮胎的不同结构部分进行材料和单元类型的定义之后,为了验证模型的正确性,将模型各方向的仿真刚度值(径向、纵向和侧向)与实验值进行对比,对比结果如表1所示[7]。可见仿真误差都小于5%,在工程允许范围内,满足后续仿真要求。
1.3 LuGre摩擦模型及其二次开发
准确地再现轮胎与路面之间力的传递情况,对研究轮胎自激振动现象至关重要。经过对比不同摩擦模型[8]的特性后发现,Canudas等[9]提出的 LuGre 摩擦模型能很好地反映摩擦过程中的“负斜率”区间以及实际摩擦接触过程中摩擦特性的动态变化现象。如图 5所示,LuGre摩擦模型假设组成干摩擦副的两物体间有无数的刷毛,并将这些刷毛看作是弹簧,摩擦力则产生于这些弹簧的弹性变形。当两物体间有相对速度时,这些刷毛最初会表现出弹簧的性质,出现弹性变形而产生静摩擦力,而后随着弹性变形的不断增大,在某一瞬间刷毛将会相对接触面产生滑移,即产生动摩擦力。
本文应用MSC.Marc提供的UFRIC用户子程序接口,用Fortran语言对LuGre摩擦模型进行了二次开发,并实现了与MSC.Marc的链接,为后面定义轮胎与路面之间的摩擦接触奠定了基础。
1.4 滚动轮胎自激振动仿真模型
在轮胎3D模型和LuGre摩擦模型建立完成后,为了更好地反映轮胎与路面的实际接触状态,针对本次仿真使用的子午线轮胎(型号为195/65R14),本文将刚性路面用半径为3.17 m(约为轮胎半径的10倍)的圆环带表示,因为实际路面也不能保证完全平整,本文所取的半径值已经远超过国标GB/T 18276-2000对滚筒半径的要求,故仿真结果能反映实际路面和胎面的接触情形。最后将轮胎模型-路面模型-摩擦模型整合成滚动轮胎仿真模型,如图6所示。
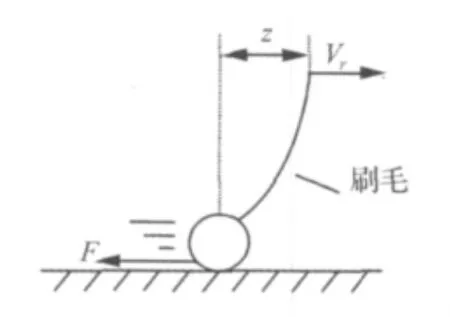
图5 LuGre摩擦模型的物理模型Fig.5 LuGre friction model
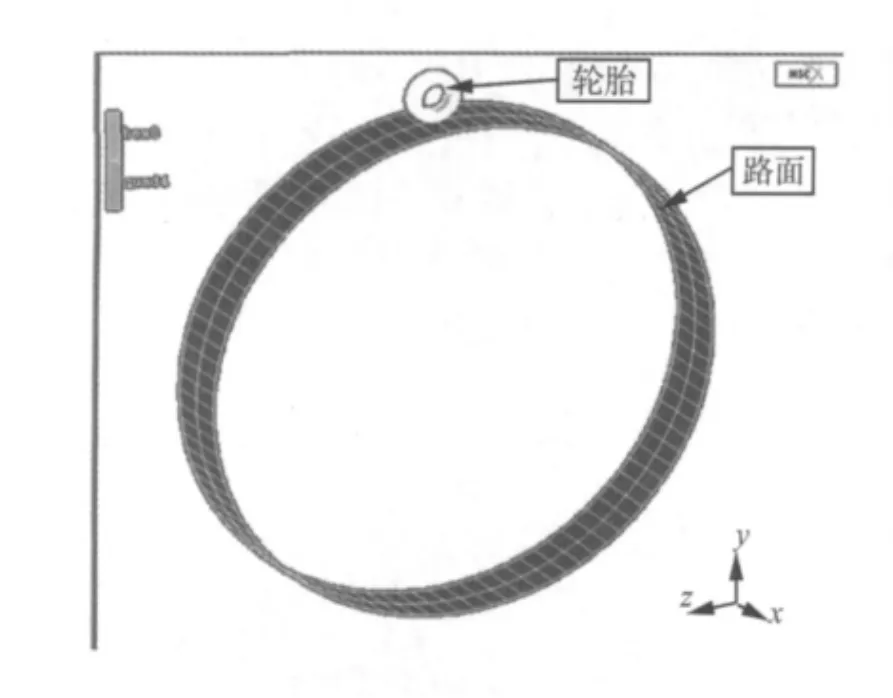
图6 MSC.Marc中轮胎-路面整合模型Fig.6 Interlinking model of tire tread and road surface in MSC.Marc
2 轮胎的工作条件对自激振动特性影响仿真分析[10-12]
在正式仿真前,要定义边界条件和载荷工况,这里将轮胎定义为可变形体,将路面和轮辋定义为刚性不可变形体。轮胎和轮辋之间定义为粘结接触(GLUE),轮胎和路面之间定义为摩擦接触,摩擦模型选用上文通过Fortran语言二次开发建立的LuGre摩擦模型。
轮胎充气状态采用在轮胎的内壁上施加均匀分布的面载荷进行模拟;垂向接触力采用限制轮胎轮辋的垂向位移,并在路面中心施加一个指向轮胎轮辋中心的垂向作用力进行模拟。
本次仿真,模拟实际试验中的底盘测功机情形,即动力由路面输入,使路面以一定的角速度转动,通过路面与轮胎之间的摩擦接触模型产生摩擦力,带动轮胎转动,实现轮胎的滚动。如图7所示,对于轮胎,我们约束住了轮辋的三向平动自由度;对于刚性路面,约束了x和z两向平动自由度,释放y向平动自由度用于施加路面与轮胎的接触挤压。
同时,在路面转动控制中心点的上方取一点,并把该点作为路面刚体运动控制的辅助控制节点。路面的中心控制节点用来施加路面刚体的平动边界条件及平动载荷,辅助控制节点与中心控制节点联合起来作用,以精确实现路面的转动运动控制。
定义完边界条件和载荷工况后,就要进行实际的轮胎滚动仿真分析,仿真所用参数如表2所示。
2.1 某一固定参数下轮胎胎面自激振动仿真分析
在表2参数下,轮胎滚动过程中某一工作步时的变形模型如图8所示。为研究胎面的自激振动现象,选取胎面上一点,提取出其在轮胎胎面x方向(侧向)上的侧向振动位移时域信号,见图9,同时提取轮胎胎面x方向(侧向)上的侧向振动速度时域信号,见图10,以及胎面与路面之间的侧向力时域变化曲线,见图11。
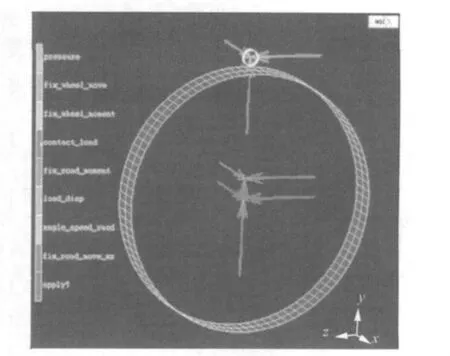
图7 轮胎和路面约束条件Fig.7 Constrains in tire-road model
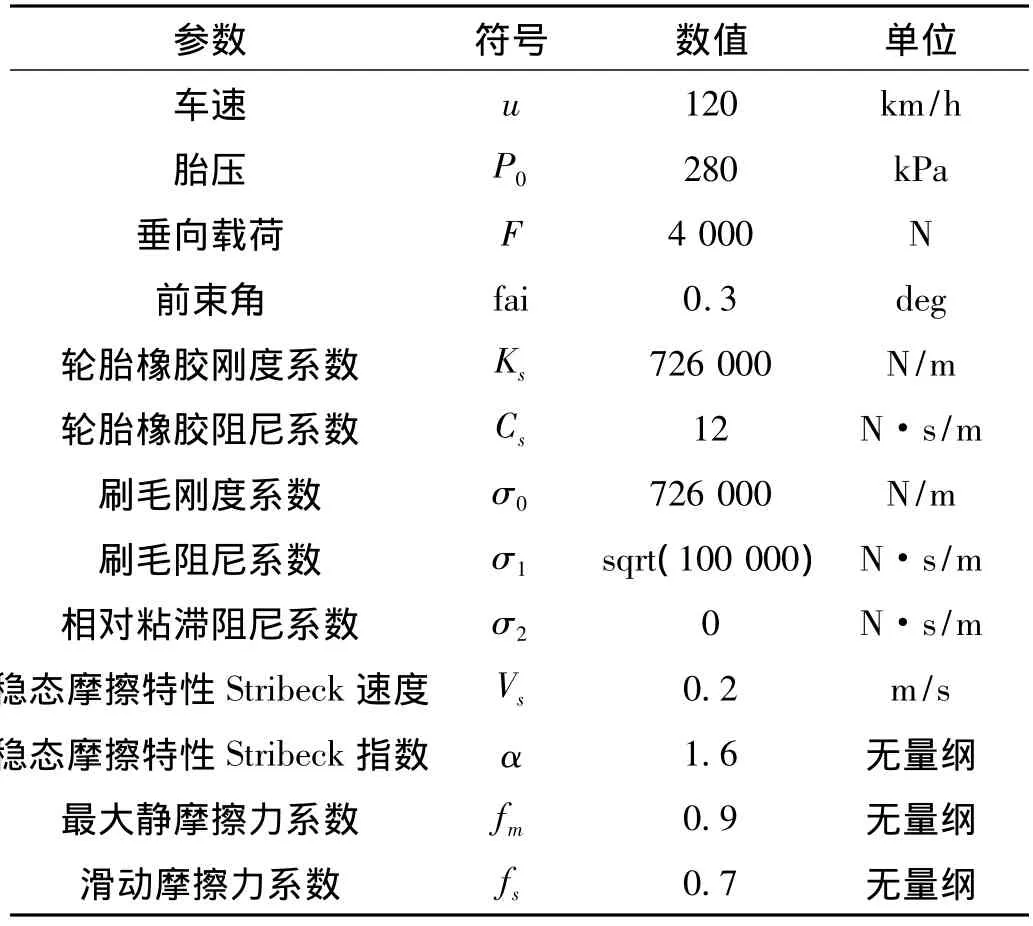
表2 仿真所用参数表Tab.2 Simulation parameters
图8 轮胎滚动过程中模型图Fig.8 Rolling tire model
从图中可以看出:
(1)胎面的侧向位移信号、侧向速度信号以及路面的侧向力信号都呈现周期性,这是由轮胎滚动的周期性所致,并且三者最终都趋于稳定;
(2)轮胎的侧向力幅值大小大致为100~200 N,这与课题组前期的研究成果相一致[9];
(3)胎面的侧向位移信号、侧向速度信号以及路面的侧向力信号在路面接触点处都有比较大的振动现象。
由于轮胎胎面的侧向位移信号、侧向速度信号以及路面与胎面之间的侧向力信号的频率成分都比较复杂,为了分析清楚其信号成分,有必要进行相应的频域分析,观察其频域特征。图12~图14所示分别为胎面的侧向位移、侧向速度以及路面与胎面之间的侧向力信号的频域特性曲线及局部放大图。
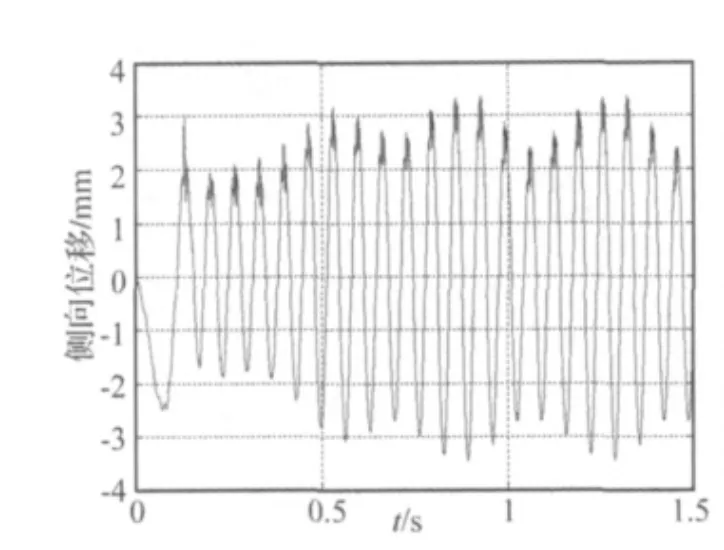
图9 胎面侧向振动位移Fig.9 Lateral tire tread vibration displacement
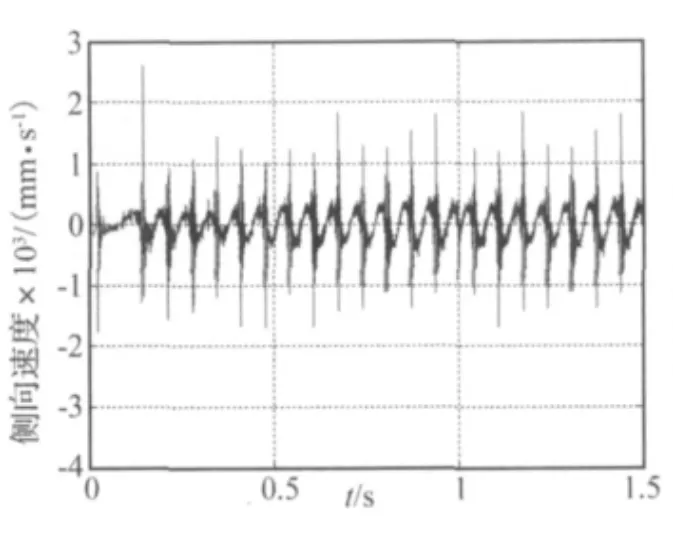
图10 胎面侧向振动速度Fig.10 Lateral tire tread vibration velocity
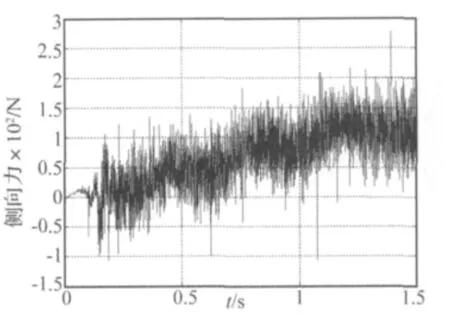
图11 路面与胎面之间的侧向力Fig.11 Lateral force between road surface and tire tread
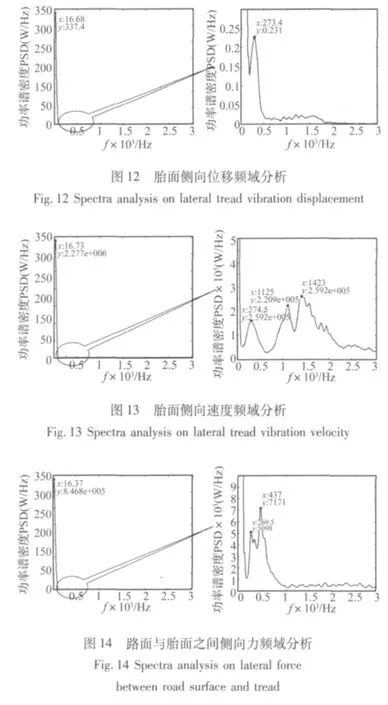
由频域分析图可以看出,在胎面的侧向位移、侧向速度和路面的侧向力信号均包含频率约为275 Hz的振动。另外,信号中有一能量比较高的低频振动成分,频率约为16~17 Hz,经计算该频率为此车速下的轮胎滚动频率。
表3~表6为在其他参数保持不变情况下,单独改变车速、载荷、前束角和外倾角时自激振动频率的变化情况。考虑到有限元仿真的数值误差,可知该频率与外界条件无关,仅由系统自身条件决定,类似于物体的固有频率。
2.2 轮胎胎面自激振动影响因素分析
轮胎多边形磨损和轮胎的自激振动是一个复杂的过程。为探讨汽车行驶工况参数(车速和载荷)和车轮定位参数(前束角、外倾角)对轮胎侧向自激振动的影响规律,本文将应用上文中的滚动轮胎仿真模型分别对其进行分析,找出各因素的影响规律,从而为控制轮胎的多边形磨损提供依据和指导[11-12]。

表3 车速变化而其他参数不变时的自激振动频率(“-”表示没出现自激振动)Tab.3 Values of the tire self-vibration frequencies with the change of speed while other parameters keep constant(“-”denotes that there is no self-vibration)

表4 载荷变化而其他参数不变时的自激振动频率(“-”表示没出现自激振动)Tab.4 Values of the tire self-vibration frequencies with the change of load while other parameters keep constant(“-”denotes that there is no self-vibration)

表5 前束角变化而其他参数不变时的自激振动频率(“-”表示没出现自激振动)Tab.5 Values of the tire self-vibration frequencies with the change of car toe-in angle while other parameters keep constant(“-”denotes that there is no self-vibration)

表6 外倾角变化而其他参数不变时的自激振动频率Tab.6 Values of the tire self-vibration frequencies with the change of camber while other parameters keep constant
2.2.1 自激振动强弱指标K
为了易于研究轮胎自激振动随车速的变化趋势,这里定义一个能反映自激振动强弱的系数K,即:
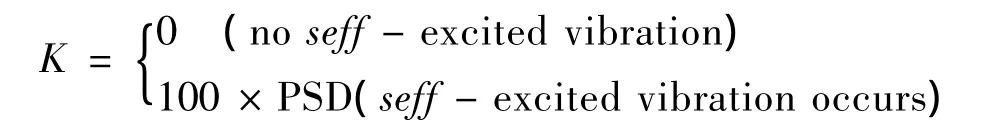
式中PSD为轮胎在自激振动频率(或共振频率)处的功率谱密度,当轮胎不产生自激振动时,定义K=0;当轮胎产生自激振动时,K值越大则表示自激振动越剧烈。
2.2.2 汽车行驶车速对轮胎自激振动的影响
考虑到轮胎的多边形磨损主要出现在高速公路上,所以在仿真过程中,车速值不小于30 km/h;同时考虑到实际中汽车的行驶速度范围,车速值也没有必要取得过大,这里选取的车速值不大于250 km/h,仿真车速见表7。

表7 仿真用车速Tab.7 Simulation velocity used
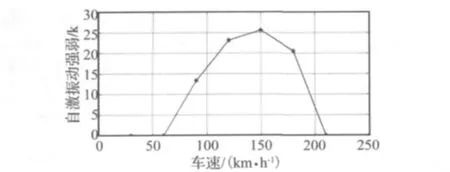
图15 车速对轮胎自激振动的影响Fig.15 Impact of speed on tire self-excited vibration
图15为不同车速下的K值,由图可知,汽车的行驶速度对于轮胎胎面的自激振动有着重要影响,车速不同,自激振动产生与否以及自激振动的强弱程度均有所不同。在表2参数下,只有当车速在60~210 km/h范围内时,轮胎胎面才能产生自激振动,车速过低或者过高时均不能产生。同时,在自激振动的车速范围内,随着车速的增加,自激振动先越来越剧烈,在达到一定车速时(本仿真条件下,车速大约在150 km/h),再随着车速的增大,自激振动剧烈程度越来越低,直到轮胎胎面自激振动消失,这与实际情况基本一致。
2.2.3 汽车载荷对轮胎自激振动的影响
为了研究汽车实际运行中的载荷大小对于轮胎的自激振动有着怎样的影响,下面将选取汽车常用的载荷工况进行对比仿真分析。仿真中的载荷变化情况见表8。
图16为不同载荷下的K值,由图可知,汽车的载荷条件对轮胎胎面的自激振动有着重要影响,在一定工况和参数条件下,随着载荷的增加,轮胎胎面的自激振动剧烈程度有增大趋势。所以车辆在实际行驶中,以满载或超载工况行驶的时间和路程越长,轮胎的多边形磨损越严重,已经产生多边形磨损的轮胎的报废速度也越快。

表8 仿真用载荷Tab.8 Simulation load used
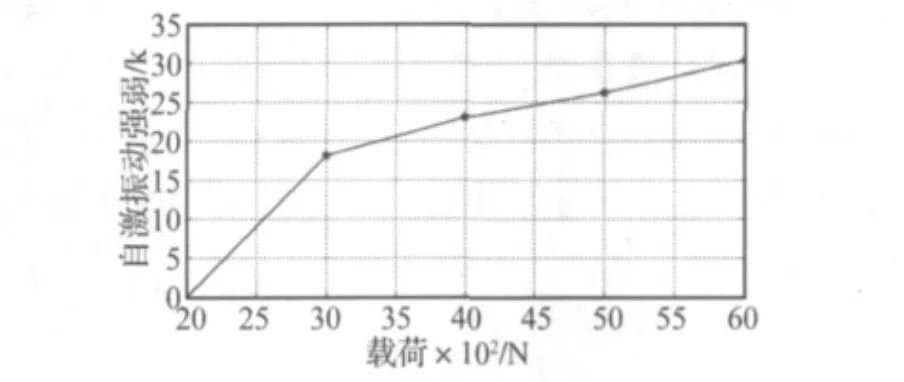
图16 载荷对轮胎自激振动的影响Fig.16 Impact of load on tire self-excited vibration
2.2.4 汽车前束角对轮胎自激振动的影响
为了保证汽车具有良好的转向特性和行驶特性,汽车转向轮设置有车轮外倾角、车轮前束角、主销内倾角和主销后倾角等四个定位参数。由于定位参数特别是车轮外倾角和前束角的存在,给汽车轮胎的实际行驶状态带来了较大的影响。试验表明,汽车轮胎的快速磨损和畸形磨损有相当一部分是由于车轮外倾角、前束角的大小匹配不合理造成的。下面将分析汽车前束角对轮胎自激振动的影响规律,所用参数见表9。

表9 仿真用前束角Tab.9 Simulation toe-in angle used
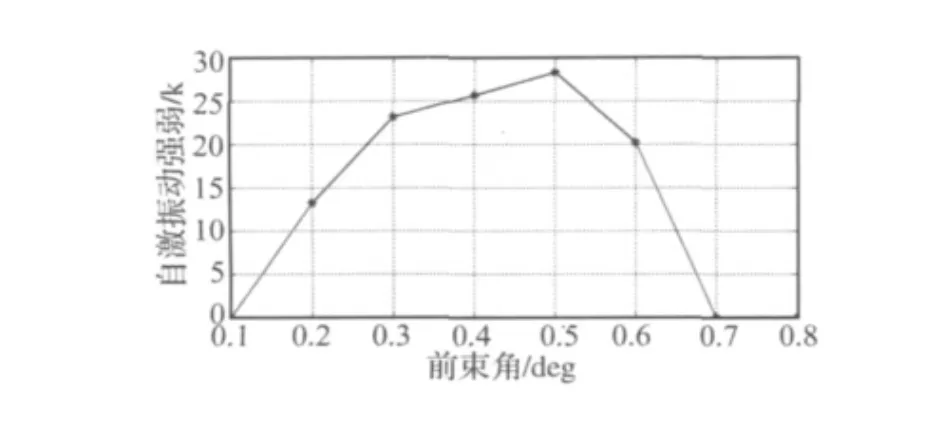
图17 前束角对轮胎自激振动的影响Fig.17 Impact of toe-in angle on tire self- excited vibration
图17为不同前束角下的K值,由图可知,汽车的前束角对轮胎自激振动的影响比较突出,在本文的仿真参数条件下,当汽车的前束角在0.2~0.6 deg范围内时,轮胎产生自激振动,且在该范围内随着前束角的增大,自激振动的剧烈程度以大约0.5 deg为界限,先逐渐增大,再逐渐减小。前束角过小或过大时,轮胎胎面并不产生自激振动,这与实际情况相吻合。
2.2.5 汽车外倾角对轮胎自激振动的影响
汽车外倾角也会对轮胎自激振动产生影响,下面将分析汽车外倾角对轮胎自激振动的影响规律,所用参数见表10。
图18为不同外倾角下的K值,由图可知,轮胎胎面的自激振动对汽车的外倾角的敏感程度虽然并不如前束角那么强烈,但也不能忽视。在一定的外倾角范围内,随着外倾角增大,轮胎自激振动有加剧趋势,当外倾角达到一定值后,轮胎胎面的自激振动将不再随外倾角的增大而加剧,而是有所下降。所以合理的选取车轮的外倾角,也可以在一定程度上控制轮胎的自激振动,进而抑制轮胎的多边形磨损。

表10 仿真用外倾角Tab.10 Simulation camber angle used
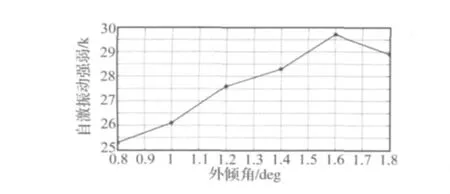
图18 外倾角对轮胎自激振动的影响Fig.18 Impact of camber angle on tire self-excited vibration
3 结论
(1)轮胎胎面自激振动属于“硬自激振动”,即只有在满足一定条件下才会出现,行驶车速、轮胎载荷以及汽车的前束角和外倾角等都是比较重要的影响因素;
(2)一定参数条件下,只有当车速在一定范围内时,轮胎胎面才能产生自激振动,车速过低或者过高均不会产生,前束角对自激振动的影响与车速类似,两者都有一个对应于自激振动的取值范围;
(3)在大载荷条件下,胎面自激振动比较剧烈,轮胎的多边形磨损也会比较严重。
根据以上分析,本文提出以下控制轮胎自激振动及轮胎多边形磨损的策略:
(1)尽量避开能够产生自激振动的行驶车速范围,避免长时间大负荷超载行驶,合理调整汽车前束角、外倾角等参数,尽量避开易导致发生自激振动的范围;
(2)其他控制策略:从轮胎的结构和材料入手,研究并改善轮胎的自激振动特性,以降低多边形磨损。
[1] 龚庆寿.机床进给系统的自激振动[J].湖南工程学院学报,2002,12(3):43-44.
[2] McMillan A J.A non-linear friction model for self-excited vibrations[J].Journal of Sound and Vibration,1997,205(3):323–335.
[3] Sueoka A,Ryu T,Kondou T,et al.Polygonal wear of automobile tire[J].JSME International Journal Series C,1997,40(2):209-217.
[4] 李 勇,左曙光,雷 镭,等.基于胎面侧向振动的轮胎多边形磨损机理分析[J].同济大学学报(自然科学版),2011,39(1):100-104.
[5] 杨宪武,左曙光,雷 镭,等.基于胎面-路面摩擦自激的轮胎非线性振动建模仿真[J].振动与冲击,2010,29(5):211-214.
[6] Zheng D.Prediction of tire tread wear with FEM steady state rolling contact simulation[J].Tire Science and Technology,2003,31(3):189-202.
[7] 王纪瑞.滚动汽车轮胎自激振动及其影响因素分析[D].上海:同济大学,2011.
[8] 彭旭东,谢友柏,郭孔辉.轮胎摩擦学的研究与发展[J].中国机械工程,1999(2):215-219
[9] Canudas D W C,Oolsson H,Astrom K J,et al.A new model for control of systems with friction[J].IEEE Transactions on Automatic control,1995,40(3):419- 425.
[10] 灰 晋,周 洁.影响轮胎磨损因素的探讨[J].轮胎工业,2002(22):629-630.
[11] Heinrich G,Kluppel M,Friction R.Tread deformation and tire traction[J].Wear,2008,265:1052-1060.
[12] 彭旭东,郭孔辉,丁玉华,等.轮胎磨损的影响因素[J].橡胶工业,2003,50(10):619-624.

