SN-分子离子的势能函数和光谱常数研究*

李 松 韩立波 陈善俊 段传喜

1)(长江大学物理科学与技术学院，荆州 434023)

2)(华中师范大学物理科学与技术学院，武汉 430079)

(2012年8月10日收到;2013年1月29日收到修改稿)

1 引言

分子离子广泛存在于等离子体系、化学反应过程、燃烧过程、星际空间之中，因此有必要针对分子离子进行相关研究.由于对分子离子的实验探测往往比较困难或者实验成本很高，所以可以利用理论计算方法探究这些体系的物理图像和机理，从而为实验探测提供有用的信息.例如通过计算得到的电偶极矩、转动常数等物理量可以模拟出体系的光谱特征，为实验研究提供有效的指导，并有助于识别天文探测中发现的谱线.

作为结构最简单的含硫—氮键负离子，SN-分子离子受到了众多实验及理论工作者的广泛关注.在实验方面，Burnett等人[9]于1982年针对SN-进行了光电子谱的实验探测，并通过对实验谱线的拟合与分析得到了该体系的平衡键长和谐振频率.在理论研究方面，Bruna和Grain[10]在实验的基础上采用MRD-CI方法结合添加了弥散函数和极化函数的DZP基组计算得到了体系的部分光谱常数.Peterson 和 Woods[11]用 MP4SDQ，CISD，CEPA-1，CASSCF等方法结合包含有101个基函数的收缩高斯型基组也开展了理论计算.Czernek和ivn[12]用CCSD(T)/cc-pVQZ方法得到的光谱常数相比之前的理论计算结果更接近实验值.此外，他们还通过基组外推确定了体系的离解能.不过，以上理论研究均没有给出解析势能函数的具体表达式，而该体系各能级的有关分子常数也无从得知.

本文采用单双迭代包括三重激发的耦合簇方法[CCSD(T)]结合系列相关一致基组[aug-ccpVXZ(X=D,T,Q,5)]对SN-分子离子分别进行了结构优化和单点能扫描计算，并将计算结果进行了基组外推.通过最小二乘拟合方法确定了体系的基态解析势能函数，并计算得到了完整的光谱常数.基于拟合所得解析势能函数，通过求解核运动的径向薛定谔方程得到了J=0时SN-(X3Σ-)的各振动态.对于每一个振动态还计算得到了相应的惯性转动常数以及离心畸变常数.本文计算的各光谱常数相比其他理论计算结果更加接近实验值，表明本文的数据具有较高的精度，能够为进一步的实验和理论研究提供参考依据.

2 SN-分子离子的离解极限

确定正确的离解极限是准确地表达分子体系势能函数的前提.根据结构优化计算以及文献[9—12]中给出的结果，SN-分子离子的基态是X3Σ-.其电子组态 1σ22σ23σ24σ21π45σ26σ27σ22π43π2是在相应中性分子电子组态的基础上由π∗轨道得到一个电子所构成.SN-分子离子为线性双原子分子，属于C∞v群，有可能离解成S-+N或者N-+S两种形式.由于S原子相比N原子具有更大的电子亲合能，所以夺取电子的能力更强，更容易形成负离子.因此SN-分子离子的离解极限应为二者中的前一种形式.N原子和S-离子的基态分别为4Su和2Pu.当二者反应生成SN-分子离子时，N和S-的对称性降低.根据原子分子反应静力学基本原理[13]，这两个原子群分别分解为C∞v分子群的不可约表示，即4Su(N)→4Σ-，2Pu(S-)→2Σ++2Π.二者的直积约化可以得到SN-分子离子可能的电子态：

可以看出结果中含有该体系的基态3Σ-.根据微观过程的可逆性原理，SN-分子离子在基态的离解极限为

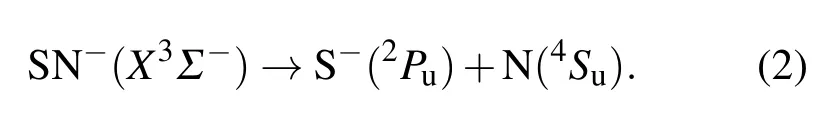
3 理论方法与计算

采用CCSD(T)/aug-cc-pVXZ(X=D,T,Q,5)方法对SN-分子离子进行了结构优化和单点能扫描计算.考虑到当前体系的结构比较简单，因此谐振频率与平衡结构的计算在相同的理论水平上进行.单点能扫描范围是0.1 nm至0.8 nm，扫描步长为0.005 nm，因此对采用的每一种基组都计算了141个数据点.为了兼顾计算的精度和效率，本文在aug-cc-pVXZ(X=D,T,Q,5)基组计算结果的基础上进行了基组外推.虽然选用更大的基组进行计算可以提高计算结果的精度，但是需要占用更多的计算资源.而基组的不完备性仍然是使计算精度受到限制的原因.选用逐渐增大的系列基组开展计算并对计算结果进行基组外推的处理方法可以减小基组截断误差对计算结果的影响，使其更接近实际值，是得到高精度结果的有效方法[14,15].本文对基于不同基组的优化计算以及单点能扫描结果分别进行了基组外推.基组外推采用如下的计算公式[15-18]：

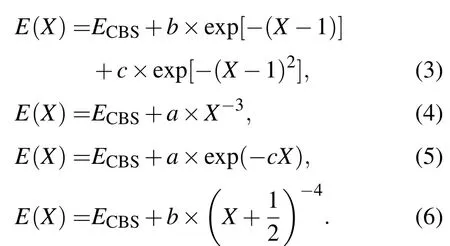
以上各式中，E(X)和ECBS分别是各基组计算所得以及基组外推的各单点能能量，X=2,3,4,5分别对应相关一致基组中的DZ，TZ，QZ和5Z.各公式中的a，b和c是拟合系数.由于研究体系的不同以及采用的基组不一样，很难确定到底哪一种外推公式更合适，因此并没有普适的最佳外推公式[19-21].由于(3)式和(5)式的外推结果往往有所低估，而(4)式和(6)式的计算结果又略为偏大，所以在实际应用中往往对两种或几种方法计算的结果取平均值[19,22,23].在本文中，将四种外推方法计算结果的平均值作为最终的外推结果，其中(3)式至(6)式的计算结果分别用CBS1至CBS4表示，四者的平均值用CBS表示.

Murrell-Sorbie(M-S)势能函数[24]被认为是能够较好地反映双原子分子势能函数的解析表达式之一.在多原子分子体系势能函数的多体展开项中，该函数也被广泛用于表示二体项[25-27].M-S势能函数由下式进行描述：

其中，ρ=R-Re，R与Re分别是核间距以及平衡核间距，De是离解能，ai是拟合参量.

在拟合得出体系的解析势能函数之后，对其求导可以计算出力常数[28].由此得到的二阶至四阶力常数可分别表示为

根据力常数与光谱常数的关系可以进一步通过下列各式求得体系的光谱常数：

式中，µ是体系的约化质量，c是真空中的光速，Be与αe分别是刚性转动常数和非刚性转动常数，ωe，ωeχe分别是谐振频率和非谐性常数，Drot是离心畸变常数.

基于结构优化以及单点能扫描的数据，利用Level8.0程序[29]通过求解双原子径向核运动的薛定谔方程，计算得到了J=0时该体系基态的所有振动能级，并进一步对各振动能级的惯性转动常数以及离心畸变常数分别进行了计算.

4 结果与讨论

4.1 基态SN-(X3Σ-)的结构参数

结构优化的计算结果列于表1，四种外推方法的各相应结果也一并列出.从表中可以看出，优化计算得到的体系平衡核间距在0.16 nm左右，相比其中性分子的平衡核间距Re(SN)=0.149402 nm[30]增大了∼6%.本文四种基组外推方法的计算结果均非常接近，即使是其中最大的CBS4与最小的CBS3也仅相差∼0.3%.而四者的平均值CBS为0.15852 nm，相比其他文献的理论计算数据更接近文献[9]的实验值0.1589(20)nm.对比的结果表明本文针对该体系的理论计算是可靠的.另外，尽管文献[12]也在CCSD(T)理论水平上进行了计算，但是本文选用aug-ccpVQZ基组计算所得Re(0.15938 nm)相比文献[12]中采用cc-pVQZ基组的结果(0.159704 nm)更接近实验值.本文基组外推得到体系的谐振频率ωe=948.05 cm-1，相对其中性分子的谐振频率1218.7 cm-1[30]减小了∼25%，表明SN在得到一个电子形成负离子之后，两原子间的键强有较大幅度的减弱.另外，本文的计算结果以及各文献计算结果均稍大于实验值.对于离解能De，本文将经零点能校正后的数据进行基组外推而得到的结果为3.934 eV，其数值相对较大.分子或离子的离解能越大，表明这些分子或离子越稳定[31].文献[10]中将Re和ωe固定于实验值计算而得结果比本文结果小∼1.0%.但考虑到实验数据的标准偏差较大，可以认为本文计算结果的精度较之文献[10]中的结果有所提高.相比之下，文献[11]的离解能与其他计算结果均有∼4.5%的偏离.而文献[12]给出的是未经零点能校正的D0的计算结果.

表1 CCSD(T)方法计算得到的基态SN-分子离子(X3Σ-)的优化结果

4.2 基态SN-(X3Σ-)的解析势能函数和光谱常数

利用四种外推方法分别对aug-cc-pVXZ(X=D,T,Q,5)计算的各组单点能进行基组外推.将四组外推结果的平均值作为在基组极限的各单点势能值.扫描计算以及基组外推的结果分别用(7)式所表示的M-S势能函数进行最小二乘拟合，得到了对应于不同理论计算水平的势能曲线.

对于(7)式中的拟合参量，截断至高次项可以改进拟合的精度[32].本文分别尝试了n=3至n=9的各种拟合方法.拟合结果显示，n的取值越大，拟合精度越高.因此，最终的拟合选取n=9.拟合结果如图1(a)所示，其中的五组离散点分别为四种基组计算以及基组外推的单点势能值，实线是分别对这五组数据进行最小二乘拟合所得势能曲线.图1(b)显示的是在平衡核间距附近的细节情况.从图中容易看出各组拟合曲线的收敛性.而且各势能曲线与离散点均符合得很好.势能曲线只有一个极小点，呈现出了稳定态的特征.当核间距大于0.4 nm时，势能曲线已经明显趋于离解极限.因此，可以认为M-S势能函数能够准确地表示当前分子离子体系的基态势能曲线.拟合得到的势能函数参量列于表2中.

图1 基态SN-分子离子(X3Σ-)势能曲线 (a)全部扫描范围内;(b)平衡核间距附近

表2 基态SN-分子离子(X3Σ-)的Murrell-Sorbie势能函数拟合参量

拟合均方根误差RMS可以用来评价拟合的质量，其表达式为[33]

其中，N是计算的单点能数据点的数量(本文取值N=141)，Vfit和Vcal分别是对应不同核间距的各单点能拟合值和计算值.各组拟合数据的RMS也在表2中列出.如表中所示，各组数据的拟合精度均远小于化学精度(不大于1.0 kcal/mol或349.75 cm-1).这不仅表明M-S势能函数非常适合于拟合当前体系的势能曲线，而且证明本文的拟合具有很高的精度，其结果是可信的.每一组单点势能值中各个数据点的绝对拟合误差可以用图2表示.尽管图中个别数据点的拟合误差较大，但是误差与该点的能量值相比还是很小的.例如，在对基组外推数据的拟合结果图2(e)中最大拟合误差位于R=0.205 nm处，绝对误差值达到了∼238 cm-1.但是由于处于此核间距时体系的能量绝对值约为12309 cm-1，拟合误差只是其大小的∼1.9%，因此可以说明本文的计算结果是准确而可靠的.

图2 势能曲线的拟合误差 (a)—(d)aug-cc-pVXZ(X=D,T,Q,5)基组计算结果;(e)四种外推方法的平均结果

根据M-S势能函数拟合参量计算的体系力常数列于表3中.从表中可见，各力常数从aug-ccpVDZ到aug-cc-pV5Z的计算数值均逐渐趋于收敛.通过(11)式至(15)式计算得到的体系的光谱常数在表4中列出.虽然各光谱常数没有相应的实验数据加以对比，但是本文结果与文献数据还是比较吻合的，而且有理由相信本文取自四种外推方法的平均值结果更加精确.以刚性转动常数Be为例，由于本文基组外推的平衡核间距Re与实验值仅相差∼0.2%，考虑到(11)式中Be与Re的对应关系，因此计算所得Be也具有较高的精度.相比之下，只有文献[10]给出了Be的计算结果，其数值与本文结果相差∼3%.但是，其ωeχe和αe的计算值相比本文和其他文献的计算结果均有较大的偏离.而对于离心畸变常数Drot，因为其与Be和ωe相关联，所以Be和ωe的准确度对Drot的结果有直接影响.与文献[11]和文献[12]中的Drot相比，本文基组外推的计算值居于二者之间.基于本文其他分子参数与文献数据的对比，有理由相信本文基组外推所得Drot更接近其实际大小.

表3 基态SN-分子离子(X3Σ-)的力常数

表4 基态SN-分子离子(X3Σ-)的光谱常数

4.3 基态SN-(X3Σ-)的振动能级和分子常数

对基态SN-各振动能级和分子常数的计算是通过Le Roy的Level8.0程序进行的.基于结构优化计算所得体系的平衡核间距、离解能，结合势能曲线扫描计算所得单点能，通过求解核运动的径向薛定谔方程计算了当转动量子数J=0时该体系电子基态所有可能的振动能级.计算过程中，在核间距位于0.1 nm至0.8 nm区间内使用三次样条插值方法进行内插计算，而在核间距小于0.105 nm以及大于0.795 nm时分别用指数函数以及幂函数进行外推.最终得到了该分子离子在电子基态的所有振动能级.在此基础上进一步计算了各振动能级相应的惯性转动常数以及各阶离心畸变常数.计算所得振动能级以及分子常数列于表5.由于篇幅所限，表5中只列出了SN-分子离子(X3Σ-)前20个振动能级G(v)以及每一个能级所对应的转动常数Bv、四阶离心畸变常数Dv和六阶离心畸变常数Hv，而略去了较高振动量子数的振动能级以及高阶离心畸变常数Lv，Mv，Nv，Ov.由于目前还没有涉及该体系振动能级的文献报道，所以本文所得振动能级以及各能级的分子常数有助于对该体系开展进一步的实验研究，并有助于在天文观测中识别源于该体系的光谱.

表5 基态SN-分子离子(X3Σ-)的振动能级和惯性分子常数(J=0)

5 结论

本文利用高精度的从头计算方法CCSD(T)以及系列相关一致基组aug-cc-pVXZ(X=D,T,Q,5)对SN-分子离子进行了平衡结构、谐振频率和单点能扫描计算，并将计算结果用四种方法分别进行了基组外推.基组外推所得平衡核间距比其他的理论计算结果更接近实验值，而谐振频率相比实验结果稍大.通过计算和外推得到的各组单点能能量用Murrell-Sorbie势能函数进行最小二乘拟合，得到了体系的势能曲线.拟合得到的解析势能函数表达式可以准确地描述该体系的几何结构特征以及势能相互作用的变化趋势.在拟合所得各参量的基础上进一步计算了体系的力常数与光谱常数.通过求解核运动的径向薛定谔方程得到了J=0时SN-(X3Σ-)的各振动态.对于每一个振动态计算得到了相应的惯性转动常数以及离心畸变常数.本文的研究结果为进一步的实验和理论研究提供了参考依据，如解析势能函数可以用于表述有关多原子分子体系势能函数多体展开式中的二体项，光谱常数可以用于预测体系的谱线强度、谱线分布等光谱特征.

[1]Chivers T 2005 A Guide toChalcogen-Nitrogen Chemistry(Singapore：World Scientific Publishing Co.)

[2]Oakley R T 1988 Prog.Inorg.Chem.36 299

[3]Roesky H W 1979 Adv.Inorg.Chem.Radiochem.22 239

[4]Bojes J，Chivers T，Oakley R T，Womershuser G，Schnauber M 2007 Binary Cyclic Nitrogen-Sulfur Anions,in Inorganic Syntheses，Volume 25(Hoboken：John Wiley&Sons，Inc.)

[5]Greene R L，Street G B，Suter L J 1975 Phys.Rev.Lett.34 577

[6]Labes M M，Love P，Nichols L F 1979 Chem.Rev.79 1

[7]Kelly P F，Woollins J D 1986 Polyhedron 5 607

[8]Chivers T，Edelmann F 1986 Polyhedron 5 1661

[9]Burnett S M，Felgerle C S，Stevens A E，Lineberger W C 1982 J.Phys.Chem.86 4486

[10]Bruna P J，Grain F 1987 J.Phys.B：At.Mol.Phys.20 5967

[11]Peterson K A，Woods R C 1990 J.Chem.Phys.93 1876

[13]Zhu Z H 1996 Atomic and molecular Reaction Statics(Beijing：Science Press)(in Chinese)[朱正和1996原子与分子反应静力学(北京：科学出版社)]

[14]Jenson F 2005 Theor.Chem.Acc.113 267

[15]Peterson K A，Woon D E，Dunning T H Jr.1994 J.Chem.Phys.100 7410

[16]Feller D 1992 J.Chem.Phys.96 6104

[17]Helgaker T，Klopper W，Koch H，Noga J 1997 J.Chem.Phys.106 9639

[18]Martin J M L 1996 Chem.Phys.Lett.259 669

[19]Dixon D A，de Jong W A，Peterson K A，McMahon T B 2005 J.Phys.Chem.A 109 4073

[20]Feller D，Peterson K A，Crawford T D 2006 J.Chem.Phys.124 054107

[21]Feller D，Peterson K A 2007 J.Chem.Phys.126 114105

[22]Balabanov N B，Peterson K A 2003 J.Phys.Chem.A 107 7465

[23]Balabanov N B，Peterson K A 2005 Theor.Chem.Acc.114 283

[24]MurrellJ N，Sorbie K S 1974 J.Chem.Soc.Faraday Trans.2 1552

[25]Kong F J，Du J G，Jiang G 2008 Acta Phys.Sin.57 149(in Chinese)[孔凡杰，杜际广，蒋刚2008物理学报57 149]

[26]Huang D H，Wang P H，Zhu Z H 2008 Acta Chim.Sinica 66 1915(in Chinese)[黄多辉，王藩侯，朱正和2008化学学报66 1915]

[27]ZhaoJ，Zeng H，Zhu Z H 2011 Acta Phys.Sin.60 113102(in Chinese)[赵俊，曾晖，朱正和2011物理学报60 113102]

[28]Zhu Z H，Yu H G 1997 Molecular Structure and Molecular PotentialEnergy Function(Beijing：Science Press)(in Chinese)[朱正和，俞华根1997分子结构与势能函数(北京：科学出版社)]

[29]Le Roy R J Level8.0：A Computer Program for Solving the RadialSchrdinger Equation for Bound and Quasibound Levels，University of WaterlooChemicalPhysics Research Report CP-663;see http：//leroy.uwaterloo.ca/programs.

[30]Huber K P，Herzberg G 1979 Molecular Spectra and Molecular Structure.IV.Constants of Diatomic Molecules(Van Nostrand Reinhold Company，New York)

[31]Wang R，Jiang G，Meng D Q，Zhu Z H 2009 Acta Phys.Chim.Sin.25 1103(in Chinese)[王蓉，蒋刚，蒙大桥，朱正和2009物理化学学报25 1103]

[32]Wang X Q，Yang C L，Su T，Wang M S 2009 Acta Phys.Sin.58 6873(in Chinese)[王新强，杨传路，苏涛，王美山2009物理学报58 6873]

[33]Wang J M，Sun J F 2011 Acta Phys.Sin.60 123103(in Chinese)[王杰敏，孙金锋2011物理学报60 123103]