PEG－GLDPC码设计与性能分析

王 平 朱宏鹏 李广侠

（解放军理工大学通信工程学院卫星通信重点实验室，南京，210007）

引 言

在深空通信中，由于通信距离的大幅增加，通信信号的自由空间传播损耗很大，接收信号的信噪比极低，通信系统所处理的信号强度极其微弱。因此，提高系统的功率利用效率是深空通信系统设计需要考虑的最重要问题之一，而信道编码则是一种有效提高功率利用率的方法。低密度奇偶校验（Low density parity check，LDPC）是一类具有稀疏校验矩阵的线性分组纠错码，目前已被许多卫星通信标准采纳，并应用到深空通信领域。例如，国际空间数据系统咨询委员会（Consultative committee for space data systems，CCSDS）推荐采用ARA LDPC用于深空通信系统，我国嫦娥二号探月任务中采用了LDPC编码，LDPC首次应用于我国深空探测领域。然而随着深空探测距离的增大和数据传输速率的提高，LDPC码将不能满足未来深空通信中高信道编码增益的需求，具有简单编码结构的QC－LDPC［1］也难以获得逼近信道容量极限的译码性能。

广义低密度奇偶校验（Generalized LDPC，GLDPC）码由 Lentmaier［2］和Boutros［3］于1999年分别独立提出，在迭代译码下具有优越的纠错性能。在GLDPC的Tanner图中，校验节点为一个线性分组码的约束，而不是单奇偶校验码，因此称GLDPC的校验节点为广义校验节点，该线性分组码被称为GLDPC的子码。最近有不少学者采用不同的子码（如BCH，RS，RM）对GLDPC进行了研究［4－7］。上述研究均以Gallager方法构造的LDPC为基矩阵，基矩阵存在大量的短环，从而影响了GLDPC的译码性能，无法满足深空通信高编码增益的要求。本文从低信噪比通信系统的设计需求出发，以提高GLDPC译码性能为目标，采用按边增大（Progressive edge－growth，PEG）算法构造规则LDPC码，然后以BCH为子码对其进行扩展，构造出 PEG－GLDPC 码。PEG－GLDPC 结构灵活，可根据系统设计需要灵活选择相应的码长和恰当的子码。采用基于比特栅格和BP算法的迭代联合译码机制，获得了较好的译码性能。

1 GLDPC介绍

传统GLDPC奇偶校验矩阵的构造可以分为两个步骤：首先采用Gallager方法构造低密度奇偶校验基矩阵Hb（N，J，n），其中N为码长，J为列重，n为行重，如图1（a）所示；然后选取子码C0（n，k），k为子码信息位长度，并将Hb每一行中的“1”用子码的校验矩阵H0的某一列替换，“0”用全零列矢量替换，如图1（b）所示。若校验矩阵为满秩，则构造的GLDPC码率为

图1 GLDPC校验矩阵的构造

若LDPC的低密度校验矩阵采用Gallager分层构造方法，也将每一层的N／n个分量码的直和称为一个超码。包含3个超码的LDPC（12，3）的Tanner图如图2所示，以Gallager方法为基矩阵的GLDPC的Tanner图如图3所示。需要指出的是，若低密度校验矩阵采用其他的方法构造，GLDPC码未必可以分解为若干超码。

图2 Gallager LDPC（12，3）的 Tanner图

图3 GLDPC的Tanner图

J＝2的GLDPC在最小距离意义上是渐近最优的［3］，因此目前构造的GLDPC多以J＝2的基矩阵构造。然而当J＝2时，由Gallager方法构造的规则LDPC码存在一定数量的4环，环长特性差，影响译码性能。改进基矩阵的环长特性则可进一步提高GLDPC的性能。PEG算法构造LDPC码时，在增加边的同时可尽力拉大最小环长，由PEG算法构造的中长LDPC码可将4环完全消除［8］。因此，本文选取PEG算法生成GLDPC的基矩阵。

2 PEG－GLDPC码构造

构造PEG－LDPC的过程就是获得其校验矩阵的过程，PEG－GLDPC的校验矩阵可以通过以下3个步骤获取：（1）根据PEG算法构造规则LDPC的校验矩阵，以其为基矩阵；（2）选取子码；（3）用子码校验矩阵的列向量替换LDPC校验矩阵中的“1”。

2.1 回退型PEG算法

PEG算法又称按边增长算法，它增加边的方法是在可选集中选择具有最少连接边的校验节点进行连接，最终构造的LDPC变量节点度分布一致，而校验节点度分布有所波动，并非严整意义上的规则LDPC。在GLDPC中，基矩阵的校验节点要求有完全一致的度分布。因此，为构造规则LDPC码Hb（N，J，n），本文提出一种回退型PEG算法。回退型PEG算法对传统PEG算法进行了修改，其主要特点是在增加新边时遵循以下两个原则：

（1）若可选集最少连接边的校验节点已达到校验节点度分布数，则选择次少连接边的校验节点；

（2）若可选集中所有校验节点都已达到校验节点度分布数，则回退一层。

2.2 PEG－GLDPC校验矩阵构造

下面举例给出（14，12）PEG－GLDPC的构造过程。如图4所示，首先采用回退型PEG算法构造（14，2，7）规则LDPC码作为基矩阵，然后将校验矩阵每行中的“1”随机用（7，4）BCH校验矩阵的列替换，“0”用三维全零列矢量替换。基矩阵同一列中的“1”需用子码校验矩阵不同的列来替换。

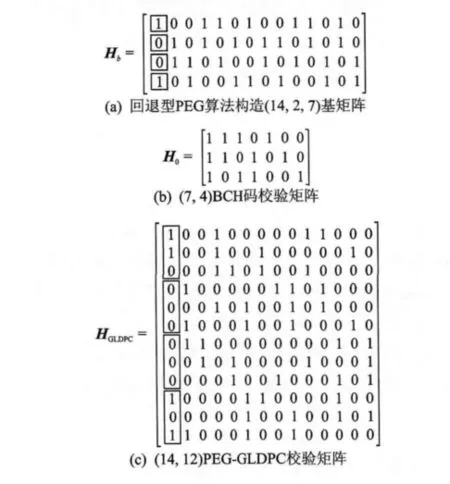
图4 （14，2）PEG－GLDPC校验矩阵的构造过程

3 联合译码算法

PEG－GLDPC码的译码分为两个层次：（1）子码的软译码，（2）基矩阵的迭代译码。受GLDPC码率和基矩阵行重的限制，GLDPC码的子码多为短码且具有高码率，可采用基于比特栅格的最大后验概率译码（Maximum a posteriori probability，MAP）算法或基于似然码字列表的Chase算法［9］进行译码。Chase算法虽然复杂度低但是次优的，为提高译码准确性本文选取MAP算法对子码进行译码。基矩阵的迭代译码选取BP算法，BP算法是一种基于似然信息传播机制的迭代译码算法。采用BCH比特栅格译码与BP迭代算法联合译码机制对PEG－GLDPC进行译码过程中，信息传递机制如图5所示。

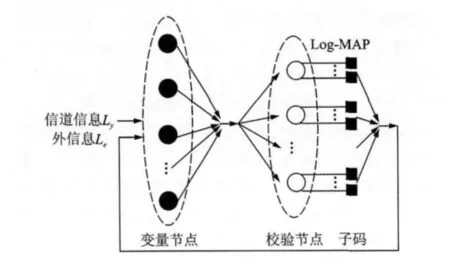
图5 PEG－GLDPC迭代译码中的信息传递机制

3.1 子码BCH的Log－MAP译码

MAP算法根据对数似然比函数（Log likehood ratio，LLR）判决每个码比特vi的值［10］，LLR定义如下

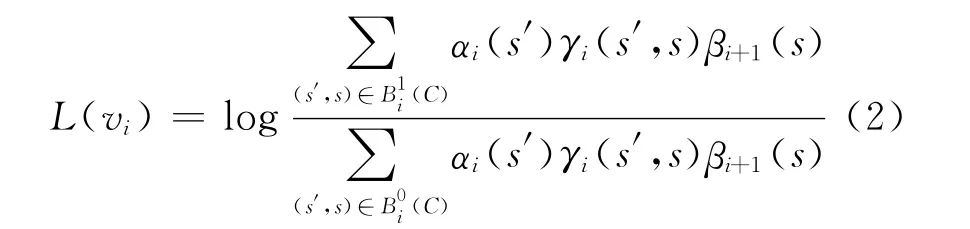
为去除式（2）中的大量乘法运算，本文采用Log－MAP译码算法，Log－MAP算法依据式（3）对式（2）进行了简化，变乘法为加法，在译码准确性下降不大的同时可降低复杂度。

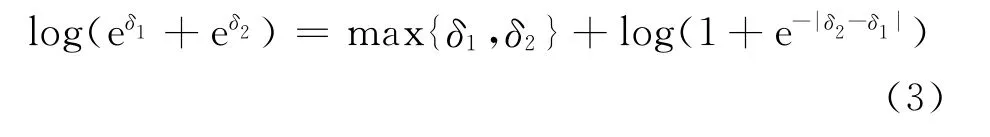
3.2 PEG－GLDPC的联合译码机制

假设发送的信息为v＝（v0，v1，…，vN－1），采用BPSK调制后，对应的双极性信号表示为c＝（c0，c1，…，cN－1），ci＝1－2vi＝±1。经过 AWGN 信道后，译码端收到的软判决信息为r＝（r0，r1，…，rN－1），r＝c＋u，其中u为均值为0、方差为σ2的高斯白噪声。变量节点的初始LLR信息可通过式（4）计算得到

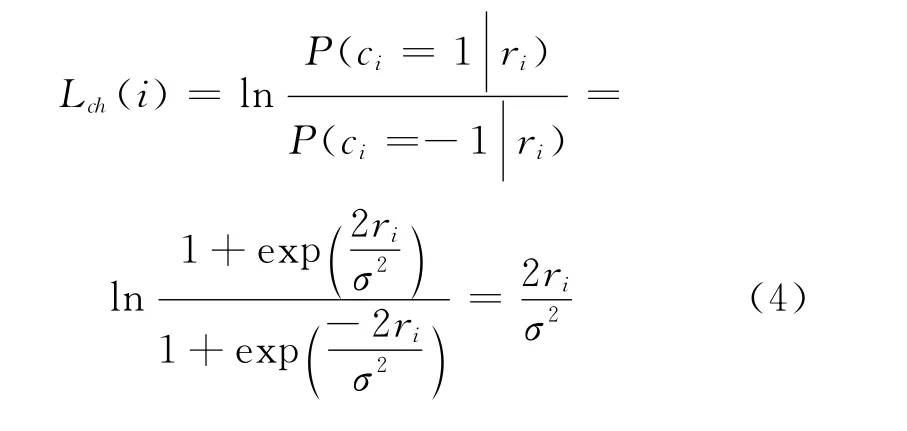
式中：Γ（i）为与变量节点vi相连的广义校验节点的集合，Λ（j）为与广义校验节点cj相连的变量节点的集合，φki（j）和ηkj（i）分别为变量节点vi向广义校验节点cj和广义校验节点cj向变量节点vi传输的LLR信息，其中t为当前迭代次数。基于Log－MAP的BP算法可以表述如下：

步骤1 初始化。通过式（4）计算每个变量节点的初始LLR信息L0（i）＝Lch（i），变量节点向广义校验节点发送初始信息值φ0i（j）＝L0（i），作为子码Log－MAP译码时的输入信息。

步骤2 子码Log－MAP译码。更新第t次广义校验节点cj对应的子码经Log－MAP译码后传输给与其相连的变量节点vi的外信息

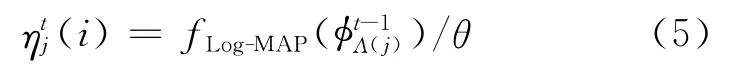
式中：fLog－MAP为子码 Log－MAP译码公式，θ为修正因子（θ＞1），用以修正Log－MAP输出的外信息值。修正因子θ目前没有既成公式，表1给出了不同的修正因子取值对码长为960的PEG－GLDPC误码率的影响。在实际应用中，需根据码长和信道条件选取恰当的θ值，进行自适应调整。

表1 修正因子对误码率的影响

步骤3 广义校验节点更新。变量节点vi向广义校验节点cj传输的外信息为

步骤4 判决。经过第t次迭代后，变量节点vi获得的后验对数似然比为

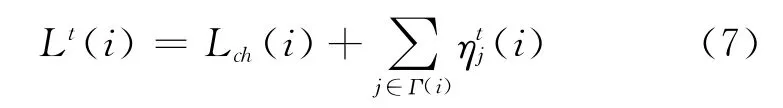
根据Lt（i）得到第t次迭代的输出序列，如果Lt（i）≥0，ci＝0；否则ci＝1。如果输出序列满足校验方程，译码成功，终止迭代，否则t＝t＋1，跳转至步骤2。

4 仿真结果与分析

在AWGN信道条件下，对PEG－GLDPC进行仿真，并与LDPC码和基于Gallager算法构造的传统GLDPC进行比较。本文选取规则GLDPC为研究对象，需要指出的若研究非规则GLDPC，需进行度分布优化设计，在用EXIT图法设计GLDPC的度分布时，需同时考虑LDPC码和子码的EXIT函数。

用PEG 算法构造（420，2，15）规则 LDPC码，并用（15，11，3）BCH码作子码进行扩展，产生的PEG－GLDPC码长为420，码率0.467。误码率曲线如图6所示，PEG－GLDPC性能优于PEG算法构造的LDPC和文献［3］中构造的传统GLDPC。同样用（15，11，3）BCH 码作子码，对PEG算法构造的（960，2，15）规则LDPC码进行扩展，得到码长960，码率0.467的PEG－GLDPC。误码率曲线如图7所示，与文献［2］中构造的传统GLDPC相比，PEG－GLDPC的误码性能明显改善。采用文献［11］中的度分布构造1／2码率的PEGGLDPC，码长为1 000 000的误码率曲线如图8所示，与 PEG 算法构造的 LDPC，QC－LDPC，传统GLDPC相比，PEG－GLDPC码的译码性能最佳，与香农限（0.184dB）距离最近。

表2给出了上述两种码字基矩阵的环长特性对比，通过表2不难发现，较之传统GLDPC，码长为960的PEG－GLDPC性能改善较大，是由于基矩阵完全消除了4环和6环，提高了BP译码的准确度。实际上，消除4环可以大幅提高译码准确度，消除6环也可以提高译码准确度，然而环长越大对译码准确度的影响越小，所以尽管码长为960的PEG－GLDPC基矩阵含有大量8环，但对译码准确度的影响已经不大。

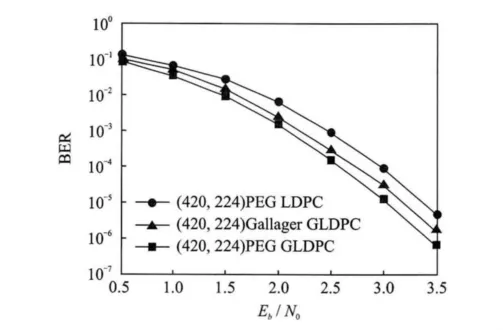
图6 （420，196）GLDPC码性能曲线

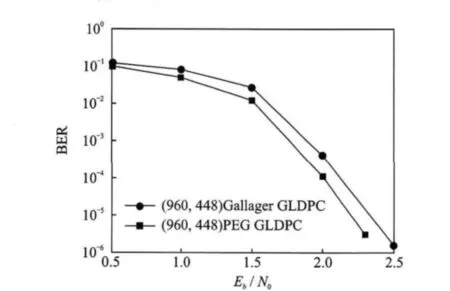
图7 （960，448）GLDPC码性能曲线

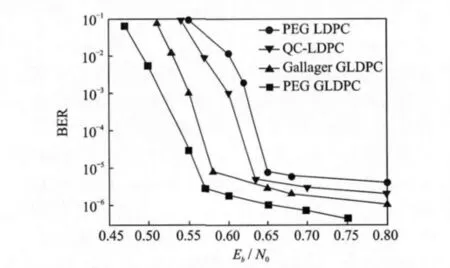
图8 1／2码率、1 000 000码长的GLDPC码性能曲线

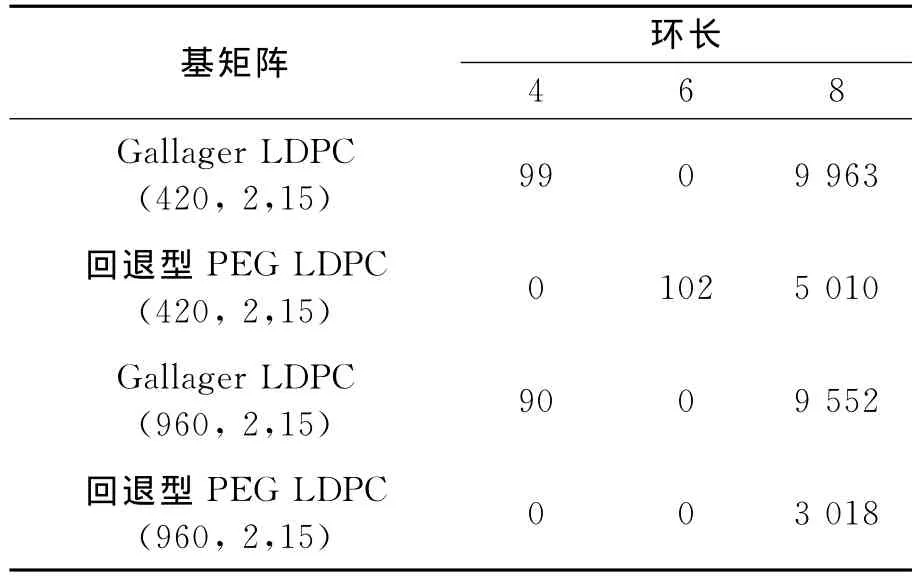
表2 基矩阵的环长特性

5 结束语

本文基于PEG算法构造了GLDPC码，并提出了适用于该码字的译码算法。对不同码长的PEG－GLDPC进行了仿真，结果表明，PEG－GLDPC的译码性能优于LDPC和传统GLDPC，适用于深空通信等点对点低信噪比通信系统。究其原因，GLDPC码采用子码校验，而不是LDPC码的单奇偶校验，因此其比LDPC码具有更强的纠错能力。而与传统GLDPC相比，PEG－GLDPC的基矩阵具有更好的环长特性，因此，其译码性能在三者中最优。本文主要从环长特性方面对GLDPC进行了改进，后续工作将研究如何从外信息、陷阱集等方面对GLDPC进行改进。

［1］ 傅婷婷，吴湛击，王文博.基于PEG算法的准循环LDPC码的编码构造方法［J］.数据采集与处理，2009，24（S1）：190－194.Fu Tingting，Wu Zhanji，Wang Wenbo.PEG－based construction method for 1uasi－cyclic LDPC［J］.Journal of Data Acquisition and Processing，2009，24（S1）：190－194.

［2］ Lentmaier M，Zigangirov K S.On generalized lowdensity parity check codes based on Hamming component codes［J］.IEEE Communications Letter，1999，3（8）：248－250.

［3］ Boutros J，Pothier O，Zkmort G.Generalized lowdensity（Tanner）codes［C］∥Proceeding IEEE ICC.Vancouver：Curran Associates Inc.，1999：441－445.

［4］ Chilappagari S K，Nguyen D V，Vasic B，et al.On trapping sets and guaranteed error correction capability of LDPC codes and GLDPC codes［J］.IEEE Transactions on Information Theory，2010，56（4）：1600－1611.

［5］ Bocharova I E，Hug F，Johannesson R，et al.Double－Hamming based QC LDPC codes with large minimum distance［C］∥2011IEEE International Symposium on Information Theory Proceedings.Saint－Petersburg：IEEE Express Conference Publishing，2011：923－927.

［6］ Yue Guosen，Ping Li，Wang Xiaodong.Generalized low－density parity－check codes based on Hadamard constraints［J］.IEEE Transactions on Information Theory，2007，53（3）：1058－1079.

［7］ Abu－Surra S，Divsalar D，Ryan W E.On the typical minimum distance of generalized LDPC convolutional codes based on protographs［C］∥ISIT 2010.Texas：IEEE Express Conference Publishing，2010：709－713.

［8］ Hu Xiaoy，Eleftheriou E，Arnold D M.Regular and irregular progressive edge－growth Tanner graphs［J］.IEEE Transactions on Information Theory，2005，51（1）：386－398.

［9］ 郑贺，陆佩忠，胡捍英.基于二分图的乘积码迭代译码算法［J］.电子与信息学报，2006，28（1）：86－91.Zheng He，Chen Peizhong，Hu Hanying.Iterative decoding algorithm for product codes based on bipartite graphs［J］.Journal of Electronics ＆Information Technology，2006，28（1）：86－91.

［10］Lin S，Costello D J.Error control coding［M］.Landon：Prentice Hall，2007：711－715.

［11］Wang Yige，Fossorier M.Doubly generalized LDPC codes over the AWGN channel［J］.IEEE Transactions on Information Theory，2009，57（5）：1312－1319.