小数乘法器的低功耗设计与实现

袁 博 刘红侠

（西安电子科技大学宽禁带半导体材料与器件国家重点实验室，西安，710071）

引 言

随着SoC（片上系统）设计的高速发展，如何降低系统功耗和面积成为越来越多设计者们共同关心的课题［1］。功耗主要有3种：即静态功耗、动态功耗和状态跳变时电源与地间的短路功耗。其中动态功耗，即电路节点电平翻转时对负载电容的充放电功耗，是电路的主要功耗源；静态功耗即当电路处于静态即状态保持不变时的功耗，在电路功耗中所占比例很小。因此低功耗设计的一个重要思想就是通过减少电路中冗余的状态翻转，实现降低功耗的目的［2］。在传统数字设计中，人们往往希望通过降低系统时钟频率、减少冗余信号翻转等方法来降低系统功耗。其中降低系统时钟频率会有效降低系统功耗，但系统性能和工作效率也会随之降低；而减少冗余信号翻转虽然不会影响系统性能，但需要在系统中增加额外控制电路，这会使得系统引入额外的功耗和面积［3］。常见的低功耗设计有：

（1）门控时钟 其主要采用触发器的设计方法，即当触发器状态出现冗余翻转时，通过关闭时序部件的时钟，使触发器保持静态，同时以这些时序部件输出为输入信号的组合逻辑也将处于静态，可以实现降低功耗的作用。该方法的缺点是需要在时序部件的时钟输入端加入控制逻辑，使其能够在部件处于冗余状态时关闭输入时钟，即在降低部件功耗的同时引入控制逻辑带来的额外功耗，影响部件低功耗优化效果。

（2）操作数隔离 其优化对象是系统中的算术、逻辑运算模块，主要方法是在系统处于冗余状态下，即不进行算术、逻辑运算的时候，使模块的所有输入保持“0”值，禁止操作数进入系统产生冗余信号翻转，该方法使系统输出结果保持静止。而当系统需要进行运算时，将模块的所有输入还原使其正常工作。该方法的缺点是需要在运算模块的输入端增加控制逻辑，使其能够在处于冗余状态所有输入信号赋“0”，但同时引入了控制逻辑带来的额外功耗，影响模块低功耗优化效果。

（3）存储器分块访问 主要方法是将系统中存储器按照其内部各子模块所需容量进行分块，然后用高位地址线进行片选译码。假设某系统分配到一块128KB的RAM，其内部两个子模块各自需要一块64KB的RAM，这时可以选用两块64KB的RAM和17位的地址线。其中低16位地址线直接提供给两个RAM，最高位地址线接到下面RAM的片选端CS。通过这种方法，不管从CPU出来什么样的地址，则每次只会选中一个64KB的RAM。如果采用单块128KB的RAM，则每次都要选中一块128KB的RAM，众所周知，一块64 KB RAM的功耗要远小于一块128KB RAM的功耗。该方法的缺点是需要将地址总线的位宽扩大，同时加入片选逻辑，使系统在降低功耗同时引入了总线扩宽和片选逻辑带来的额外功耗，影响系统的低功耗优化效果。

随着超大规模集成电路设计技术的进步，高性能信号处理芯片已经成为通信、电子、空间技术等领域必不可少的组成部分，因此如数字滤波器及数字信号处理器等含有大量小数乘法运算的模块也频繁地被应用于各种芯片和电路中［3］。对于小数乘法运算而言，为了保持较高的运算精度，要求寄存中间运算结果的寄存器保留较宽的位宽，但系统功耗和面积也会随之增大；如果试图减小寄存器位宽，乘法运算的精度损失则不可避免［4，5］。

本文的目的在于针对上述已有技术的不足，提出一种针对小数乘法运算的低功耗设计算法，该算法的优点在于：（1）采用了一种全新的设计和实现方案，使得综合后只有优化结果参与生成系统门级电路，而优化算法自身的逻辑单元不会引入到系统中。对于含有大规模乘法运算的系统，避免其内部各乘法器引入优化逻辑自身的功耗和面积累加入被优化系统，提升优化效果。（2）由于在运算过程中只需搜索乘法器系数中“1”的排列和位置并加以计算［5］，因此具有运行速度快，占用资源少，简单易行的优点。（3）该设计能够在不降低系统工作效率、不损失运算精度、不增加额外逻辑单元的条件下，大幅降低系统功耗和面积。

1 数据宽度优化

数字设计中，数据宽度n所能表达出的最大数被归一化为“1”，小数则被表示为所占该“归一化1”的比例，因此n位的小数B可以被整数化处理为X［6］

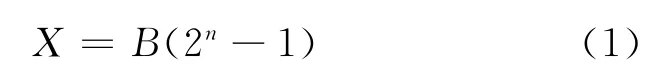
整数乘法运算A×B的计算过程如式（2）所示，其中被乘数和乘数分别为A和B，B以二进制表示为b3b2b1b0

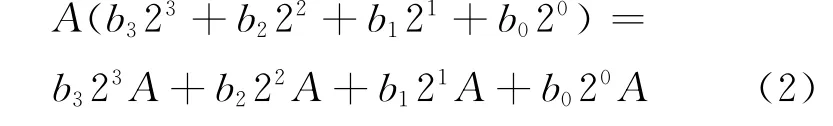
提出系数b0后，式（2）可转化为

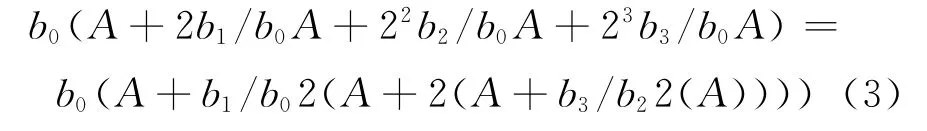
由式（3）可得，如果b0为“0”，则bi2iA项也为“0”。因此对于每一项，其分母必为“1”，否则整个项均为“0”。由此可得多项式

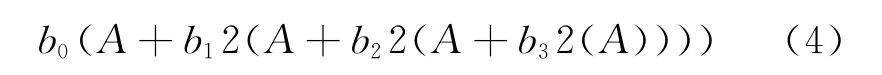
其等价多项式

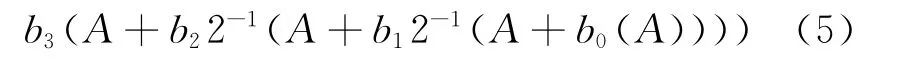
由式（5）可以看出本级加法结果的末位不参与下级加法运算，依然作为下级加法结果的末位存在。如果能够缺省本级加法结果的最末i位（i等于下级加法运算中另一个加数的左移位数），则可以减少下级加法结果的位宽，而缺省掉的也只是“最小贡献位”［7，8］。在小数乘法运算中，为了保持数据宽度，这些“最小贡献位”会在最终运算结果中被缺省掉，但不能在中间各级加法结果中缺省，否则会出现较大的误差累积从而影响运算精度和准确度。若能预先计算出各级加法结果中的“最小贡献位”进而缺省，从而降低各级加法结果位宽，而且保证最终运算结果的一致性，不损失任何运算精度和准确度［9］。

以8位小数乘法153×31／255为例，依式（1）整数化处理为153×31，其乘法竖式如图1所示，结果小数化处理并保留8位数据宽度为10010.100b。对该乘法依式（5）进行优化，缺省各级加法结果的“最小贡献位”后的乘法竖式如图2所示，结果小数化处理并保留8位数据宽度同样为10010.100b。该乘法运算转化为4个加法器，优化前其内部加法结果位宽分别为9，11，12，13，优化后其内部加法结果位宽分别为8，9，9，9。因此在乘法运算153×31／255内部共节省寄存器位宽（9＋11＋12＋13）－（8＋9＋9＋9）＝10位。对含有大量小数乘法运算的系统，优化效果将十分明显。

图1 153×31的乘法竖式

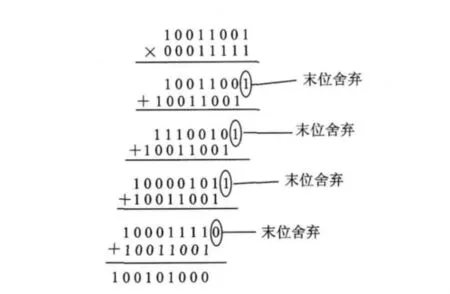
图2 缺省优化过程

2 优化算法实现及仿真

图3是n位小数乘法A×B的优化算法实现框图，首先对小数系数B整数化处理为X，对整数X从最低位向最高位搜索，逢“1”则记录其位置，以变量position－of－1表示；逢“0”则继续向高位搜索。将以上过程实现为一个VHDL函数findmulti－factor－f（x），并放入库中与系统分离，函数的输入x为乘法器的小数系数，输出为表示系数中各“1”位置的变量position－of－1，记为findmulti－factor－f（x）＝position－of－1＝（n1，n2，…，nk）。因此乘法器被转化为k－1个加法器，第一个加法器是由被乘数A左移n1位加A左移n2位构成，并缺省加法结果的最末n2位存入寄存器作为第一个中间结果A1；第i个加法器是由A左移ni位加前一个中间结果Ai－1构成，并缺省加法结果的最末ni位存入寄存器作为第i个中间结果Ai，以此类推直到构建出k－1个加法器。最后需要对加法运算结果进行小数化处理，由于算法开始先对n位小数乘法器A×B中小数系数B进行了整数化处理，相当于将B左移n位，因此最后一级加法器的结果需要右移n位还原回小数后得到最终乘法结果。然而在优化过程中最大缺省位为nk，即在优化过程中已经右移了nk位，所以最后一级加法器的结果只需右移n－nk位并由z－o输出。

设计优化乘法器模块mtplr－mutiplication，其类属参数为multi－find－g输入端口为x－i与n，输出端口为z－o。其中小数乘法器系数由模块类属参数multi－find－g输入，被乘数由x－i输入，数据宽度由n输入，最终乘法运算结果由z－o输出，图4所示为该优化乘法器模块的实体。

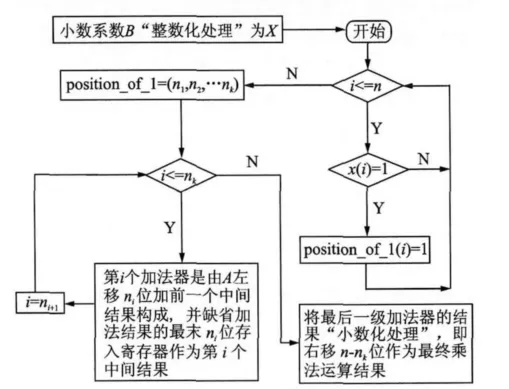
图3 优化算法实现框图

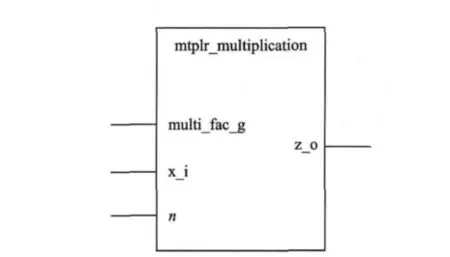
图4 优化乘法器模块mtplr－multiplication的实体

在模块内部，调用函数find－multi－factor－f（x），并使优化乘法器模块的类属参数 multifind－g作为该函数的输入，即find－multi－factorf（multi－find－g），输出结果以常数阵列shiftbits－c表示：constantshift－bits－c：nature－array：＝find－multi－factor－f（x）.position－of－1其与被乘数构建移位加法运算并且进行优化。

在综合初期，常数shift－bits－c会根据乘法器系数计算得出。综合后，乘法器仅仅根据这些常数便可转化为对应的移位加结构并进行优化，而库中的运算逻辑自身不会引入乘法器，而且优化算法是缺省对下级加法无进位贡献的本级加法结果的末位，从而减少存放各级加法结果的寄存器位宽。因此在联合优化乘法器模块mtplr－multiplication内部，没有引入任何额外的运算和逻辑单元。

将优化乘法器模块mtplr－multiplication置于库中与系统设计分离。在系统设计中实例化该模块并替换掉原有各定系数乘法器，替换时只需将各实例化模块的类属参数设定为所对应乘法器系数即可完成该系统的优化。系统设计的参数和特性一旦确定，其内部各乘法器系数也将确定。而乘法器系数由类属参数传入而不以常数参数传入的原因是：常数只能从设计实体的内部得到赋值且不能再改变，而类属的值可以由设计实体外部提供，因此设计者可以从外面通过类属参量的重新设定而容易地改变该模块的内部电路结构，即在替换时只需将各乘法系数通过类属参量传入模块便可实现不同的优化乘法器，图5所示为替换8位小数乘法y＝31／255x的优化乘法器。153×31／255的优化乘法仿真波形如图6所示，其中乘法系数multifind－g为0.121 569，即31／255；被乘数 x－i为153；位宽n为8，乘法器内部4个加法运算结果A1，A2，A3，A4分 别 为 11100101b，100001011b，100011110b，100101000b，最终8位运算结果z－o为18.5，即10010.100b，与图2运算结果一致。

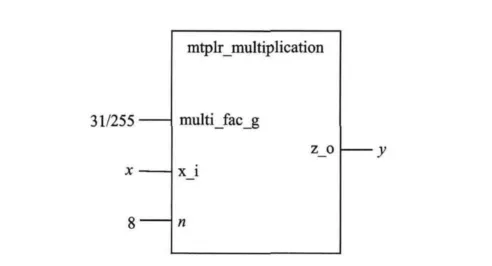
图5 替换小数乘法y＝31／255x的优化乘法器

图6 小数乘法153×31／255的优化仿真波形

3 优化效果验证

为了精确测试优化指标，以某含有大量数字滤波器和数字信号处理器的射频模块作为测试对象进行优化。测试工具为Sequence Design公司的Power Theater，作为标准功耗计算工具，它可以对系统的前端RTL代码计算出准确的功耗和面积。表1，2为优化前射频模块功耗与面积；表3，4为该射频模块经一般优化后的功耗与面积，即使用优化算法优化各乘法器，但优化逻辑存在于各乘法器中；表5，6为该射频模块经本文所述设计方案优化后的功耗与面积，即模块内部所有小数乘法器均被优化乘法器模块mtplr－multiplication替换，且优化逻辑不引入各乘法器。可以看出，优化前模块的功耗为10.7mW，逻辑单元数为95 962，面积为1.479mm2；经一般联合优化设计方案优化后，以上参数分别为9.87mW，89 190，1.457mm2，分别降低7.76%，7.06%，1.49%；经过本文所述设计方案优化后，以上参数分别为8.69mW，84 915，1.312mm2，分别降低18.79%，11.51%，11.29%，优化效果明显。

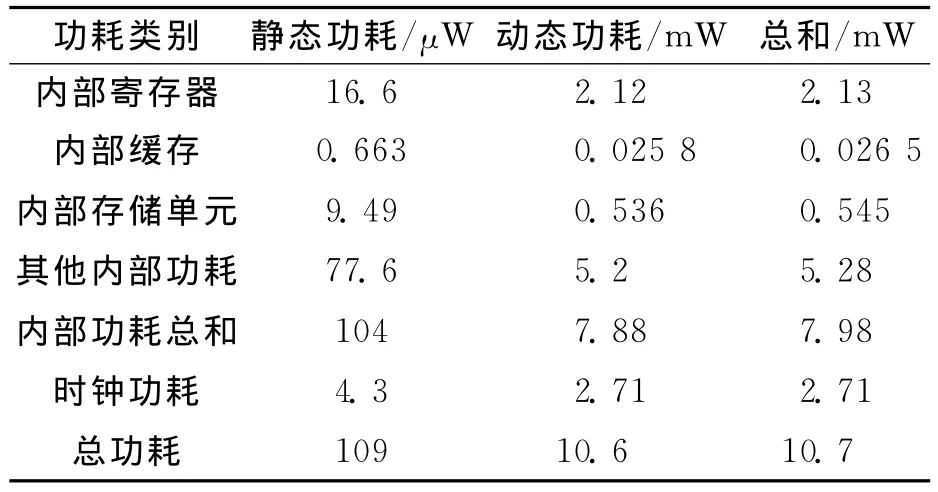
表1 优化前射频模块功耗

表2 优化前射频模块逻辑单元数和面积

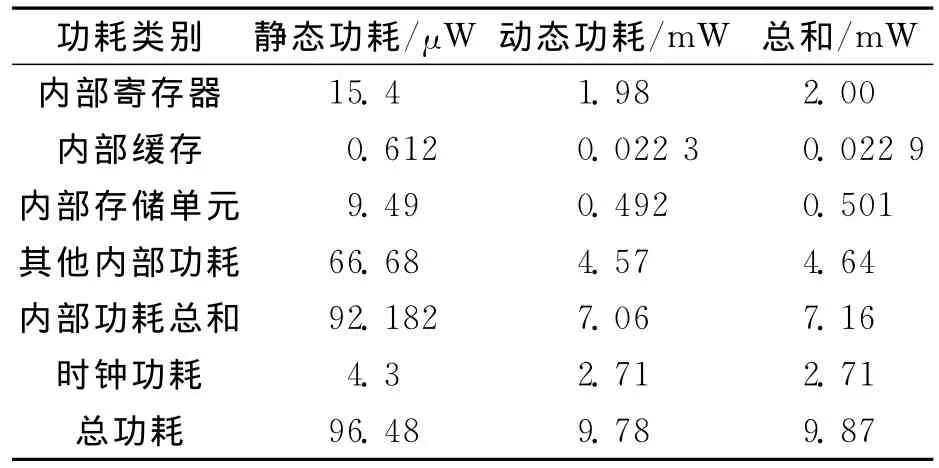
表3 射频模块经一般优化设计方案优化后的功耗

表4 射频模块经一般优化设计方案优化后的逻辑单元数和面积

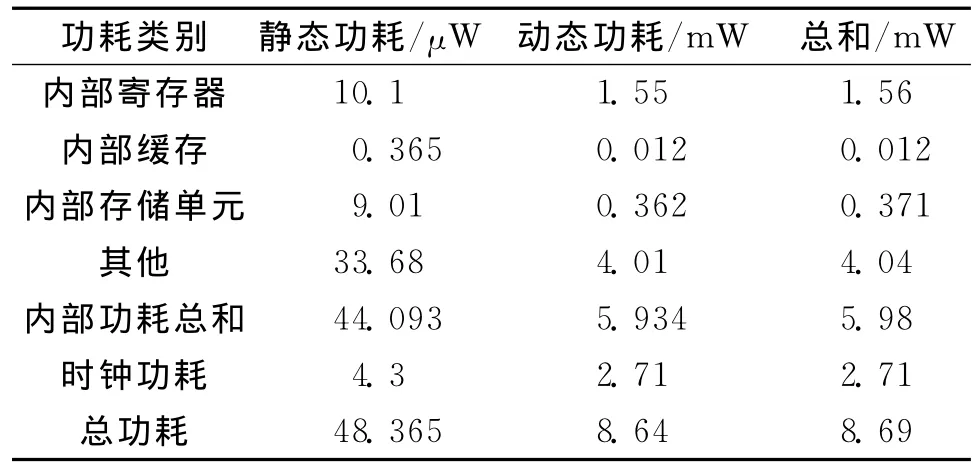
表5 射频模块经本文所述优化设计方案优化后的功耗

表6 射频模块经本文所述优化设计方案优化后的逻辑单元数和面积

为了进一步测试本文所述优化设计方案的硬件优化效果，分别对优化前的射频模块和经一般联合优化设计方案优化后的射频模块以及本文所述优化设计方案优化过的射频模块分别进行FPGA测试。测试采用StratixⅣ家族EP4SE820F43C3型号FPGA作为测试平台。

测试采用QuartusⅡ作为FPGA的编译、综合工具，该工具来自于ATERA公司，并且作为业内普遍认可的一种FPGA开发工具。优化前射频模块对该FPGA的逻辑占用率为5.6%，生成寄存器总数为18 175，存储单元占用率为6.5%；经一般联合优化方案优化过的射频模块对该FPGA的逻辑占用率为5.1%，生成寄存器总数为16 805，存储单元占用率为5.9%，分别降低8.9%，7.5%和9.2%；经本文所述优化方案优化过的射频模块对该FPGA的逻辑占用率为4.6%，生成寄存器总数为12 600，存储单元占用率为5.1%，分别降低17.9%，30.7%和21.5%。FPGA测试结果对比明显，证明本文所述优化设计方案解决了一般优化设计中优化逻辑自身被引入系统的问题，提升了系统优化效果。

4 结束语

本文提出了一种针对小数乘法器的低功耗算法，对射频模块的功耗分析和FPGA测试结果表明该算法对含有大量乘法运算的系统优化效果十分显著，而且解决了目前低功耗设计中算法自身的逻辑单元被引入系统从而降低系统优化效果的问题。

［1］ Graillat S，Langlois P，Louvet N.Compensated horner scheme［R］.University of Perpignan，France，2005：10－26.

［2］ Wong A C W，Kathiresan G，Chan C K T，et al.A 1Vwireless transceiver for an ultra low power SoC for biotelemetry applications［C］∥ 33rd European Solid State Circuits Conference.Abingdon：Toumaz，2007：127－130.

［3］ 肖玮，涂亚庆，刘良兵，等.一种频率估计的倍频等长信号加权融合算法［J］.数据采集与处理，2012，27（1）：74－79.Xiao Wei，Tu Yaqing，Liu Liangbing.A long signal of a frequency estimated multiplier weighted fusion algorithm［J］.Journal of Data Acquisition and Processing，2012，27（1）：74－79.

［4］ Malvar H S，Hallapuro A，Karczewicz M.Low complexity transform and quantization in H.264／AVC［J］.IEEE Transactions on Circuits and Systems for Video Technology，2003：13（7）：598－603.

［5］ Kang S M.Elements of low power design for integrated systems［C］／／Proceedings of the 2003International Symposium on Low Power Electronics and Design.Seoul，Korea：［s.n.］，2003：205－210.

［6］ 罗柏文，万明康，于宏毅.两种基于自适应相位补偿的FDOA估计算法［J］.数据采集与处理，2012，27（1）：20－26.Luo Baiwen，Wan Mingkang，Yu Hongyi.Two kinds of estimation algorithm based on adaptive phase compensation FDOA ［J］.Journal of Data Acquisition and Processing，2012，27（1）：20－26.

［7］ Samueli H.An improved search algorithm for the design of multiplierless FIR filters with power－of－two coefficients［J］.IEEE Transactions on Circuits and System，1989，36（7）：1044－1047.

［8］ Yoo H，Anderdon D V.Hardware－efficient distribu－ted arithmetic architecture for high－order digit filters［C］／／Proc IEEE International Conference on Acoustics，Speed and Signal Processing.［S.l.］：IEEE，2005：125－128.

［9］ Brickell E B.A fast modular multiplication algorithm with application to two key cryptography［C］／／Proceedings of Crypto 82.New York：Plenum，1982：51－60.