蚂蚁算法在FIR数字滤波器优化设计中的参数
张俊杰 仰继连
(1.洛阳师范学院物理与电子信息学院,洛阳,471022;2.清华大学电子工程系,北京,100084)
引 言
有限冲激响应(Finite impulse response,FIR)数字滤波器在语音、谱分析等数字信号处理领域有着广泛的应用。本质上FIR数字滤波器的优化设计问题是一个多变量求极值的过程。这些年来其优化设计一直受到研究人员的广泛关注。在过去的几十年里发展了大量针对FIR数字滤波器优化设计的方法,如混合整数线性规划法[1]、有界分支技术[2-4]、模拟退火算法[5]、遗传算法[6]等。
20世纪90年代初期,Dorige等人[7]通过模拟真实蚁群觅食时寻求最短路径的原理提出了蚂蚁算法(Ant algorithm,AA),这是一种新型的基于种群演化的启发式优化算法。该算法是一种本质并行的优化算法,具有鲁棒性强、易于和其他算法结合以及适于并行处理等优异性能,因此自问世以来就受到了广泛的研究,已成功应用于有源滤波器比例积分 (Proportion integration,PI)参数优化[8]、自适应抗干扰天线[9]、模型参数估计[10]、FIR数字滤波器优化设计[11-12]等领域。蚂蚁算法本身涉及参数较多,将其应用到不同领域时为了具有更好的算法性能,必须考虑如何合理地综合配置这些参数。近年来研究人员从不同方面进行了蚂蚁算法参数配置的研究和总结,主要分为两个方面:基于经典的旅行商问题(Traveling salesman problem,TSP)的仿真研究[13-18]和基于具体领域的应用研究[19-20]。总体上这些研究和总结仍是以TSP问题为测试平台,这就给具体应用领域中蚂蚁算法的参数选取带来一些指导上的不便,因此需要考虑蚂蚁算法在具体应用领域的参数选取基础上,希望能够得到相对一般的参数选取指导原则。
针对基于蚂蚁算法的FIR数字滤波器优化设计模型,本文对其中不同参数的作用和影响作了理论上的分析,研究了相关参数的最佳配置,并进一步推导出一般的参数配置公式,这将有利于蚂蚁算法的拓展和应用推广。
1 基于蚂蚁算法的优化设计
具有严格线性相位的N阶FIR数字滤波器的频率响应函数可表示为
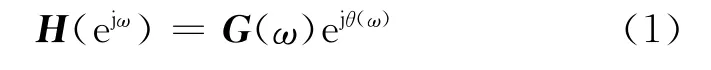
式中:G(ω)为滤波器的增益,θ(ω)为相位响应。不失一般性,本文仅讨论奇数长度偶对称低通滤波器的情形,相应的最小最大准则下优化设计问题可表述为
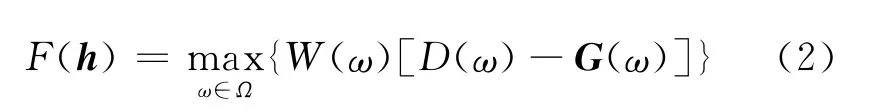
式中:D(ω)表示期望的滤波器幅度响应;Ω表示设计所需考虑的频带;W(ω)表示频带加权函数,一般为非负的常量值;h表示滤波器系数组成的向量。
对频带Ω进行离散化,记离散点集合{ωi|i=1,2,…,M},则式(2)有如下形式
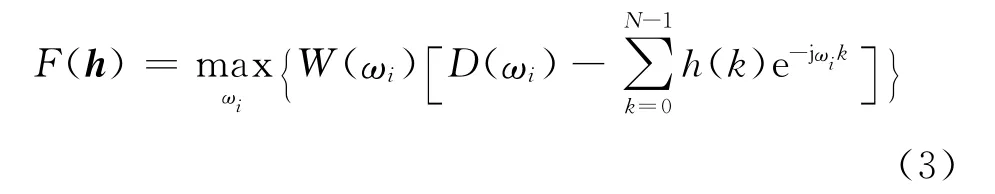
一般而言,在滤波器设计中选择M≥4N即可保证足够的精度。
将滤波器的无限精度系数h(k)用二进制进行编码,表示为I1I2I3…,其中Ii∈{0,1}。引入字长的限制条件,假设字长为b(包含符号位),则此时h(k)表示为I1I2…Ib-1。考虑到|h(k)|≤1,再引入比例因子S=2b-1,将系数以整数形式表示,有
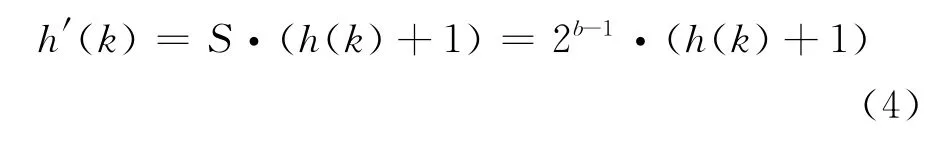
因此优化设计中系数的定义域范围为
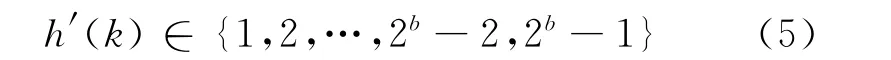
即为滤波器优化设计的系数空间。
设sij为蚂蚁i在搜索过程中取值为j时式(3)的计算结果,则启发因子定义如下

在t时刻蚂蚁i选取j值的状态转移概率可表示为
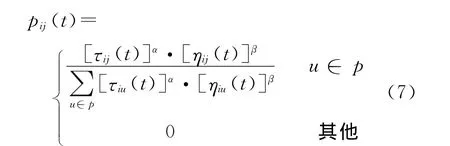
式中:τij(t)为t时刻蚂蚁i在系数空间中的信息素强度;p表示蚂蚁i选择的可能值集合;α,β分别表示信息素强度和启发因子在系数寻优中的相对重要性。
随着时间的推移,以前积累的信息素会因挥发而逐渐减少,用参数ρ表示信息素的挥发程度。所有蚂蚁完成一次寻优后,信息素强度根据式(8,9)进行调整

式中:Q为常量,体现信息素的反馈作用。
优化设计中,采用F(h)作为目标函数,利用蚂蚁算法优化设计得到一组系数,求解它的最小值,以达到技术指标的要求。为了提高算法效率,可根据技术指标在通带和阻带施加适当的约束,以避免在一些性能较差点附近搜索。
2 算法参数的配置
2.1 参数影响分析
从寻优机制不难看出,蚂蚁算法中对性能有着直接或间接影响的参数有m,α,β,ρ,Q和τij(0)。本文中,算法模型设定蚂蚁数量等于需要优化的滤波器系数个数,因而不考虑m的配置情况。算法中其他参数之间是相互关联的,有着复杂的关系,它们的取值对算法的性能和收敛性有着重要的影响。
α,β作为信息素强度和启发因子不同重要性的体现,关键是看二者的比值,因而不妨在算法中设定α=1,只需改变β值即可实现二者不同重要性的对比。如果β<1,则信息素对蚂蚁的寻优影响较大,算法陷入局部信息最优的可能性增大;反之,则陷入局部启发因子最优的可能性较大。
ρ对算法的全局搜索能力及其收敛速度有着直接的影响。如果过大,则信息素挥发得太快,不利于信息的正反馈,虽然此时能提高算法的全局搜索能力,但会使收敛性降低;反之,若其过小,则以前寻优到的值被再次选择的可能性增大,算法陷入局部最优的可能性增大,影响了解的质量。
Q作为反馈量,其值越大,正反馈作用越强,算法的收敛性越高,但同时也会使得搜索空间减小,陷入局部最优的可能性加大;反之,若其值过小,则会产生类似于ρ过大时的结果。因而Q对算法性能的影响有赖于其他参数的配置。
τij(0)取值和参数Q有着密切的联系,因为反馈量的大小都是相对于已有的信息素强度而言。虽然信息素强度随时间而变化,但初始信息素强度对它有着直接的影响,进而影响着算法的性能。
一般来说,上述参数可通过反复试凑得到较好的组合,但若想彻底分析各参数组合的性能,则会因实验组数的增加而变得不切实际。更重要的是,这些参数本质上相互联系,具有复杂的关系,仅取这些粗糙的值进行组合,难以找到参数的最佳组合,不利于提高算法的效率和收敛性。通过以上对算法参数的讨论,本文推导出一种较为有效的参数配置基本公式。
2.2 参数配置公式推导

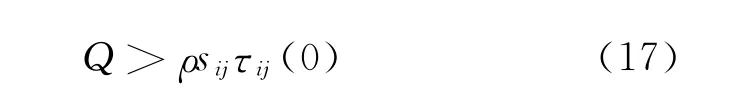
在蚂蚁算法不同的应用领域中,sij的定义会有所不同,但是在算法参数选择和配置时,ρ和τij(0)可以根据经验设定,于是有

在本文的优化设计中,根据技术指标在频带施加不同的约束,避免了在性能较差点附近的搜索。sij在系数为最优解和舍入解时差别不是很大,因而可选取滤波器系数为舍入解时式(3)的计算结果作为sij的值,这可使得其他参数更容易控制。同时,根据算法的正反馈机制,在利用式(17)进行参数配置时还应注意:不要在t比较小时就出现τij(t)≫τij(0)的情况,也不要出现t足够大时仍有τij(t)≈τij(0)的情况。只有根据实际问题进行合理的配置才能使算法具有更好的性能。
3 仿真结果分析
本文仿真实验主要验证蚂蚁算法在FIR数字滤波器优化设计中各个参数的不同配置对算法性能的影响以及参数配置公式对于参数选择的指导意义。在优化设计中本文算法的具体性能以及与其他算法的性能比较可以参见文献[11],其中在最小最大准则下本文算法与模拟退火算法相比在通带衰减性能上有了明显的提高,在最小平方准则下无论在通带还是阻带,本文算法设计的滤波器性能都比Tabu优化算法有了较大的改进,在纹波约束最小平方准则下,本文算法和离散拉格朗日乘子法优化设计所得的滤波器在阻带最小衰减和通带最大衰减效果几乎一致,满足了设计要求的技术指标,显示了本文算法在复杂准则下优化设计的良好性能。为了便于比较参数配置对算法性能的影响,本文不失一般性地在最小最大优化准则下进行仿真实验,使用MATLAB语言实现算法程序,所用硬件平台为主频2.40GHz的奔腾 Ⅳ处理器、256 MB内存的PC。仿真实验所用的FIR低通数字滤波器技术指标为:字长b=8,阶数N=51,归一化通带频率为[0,0.2],阻带频率为[0.25,0.5],通带、阻带加权函数分别为1和10。
仿真实验中,蚂蚁算法参数设置为:Q=1,ρ=0.3,τij(0)=5,滤波器系数取舍入解时sij=0.492 3,阻带衰减为26.15dB。每组实验方案运行10次,每次进行15次循环。阻带最大衰减表示10次运行中阻带衰减最大的情况,即优化性能最好情况;阻带最小衰减表示10次运行中阻带衰减最小的情况,即优化性能最差情况;阻带平均衰减表示10次仿真实验中阻带衰减的平均值;阻带衰减方差表示10次运行中阻带衰减的稳定性;平均时间表示10次仿真实循环。阻带最大衰减表示10次运行中阻带衰减最大的情况,即优化性能最好情况;阻带最小衰减表示10次运行中阻带衰减最小的情况,即优化性能最差情况;阻带平均衰减表示10次仿真实验中阻带衰减的平均值;阻带衰减方差表示10次运行中阻带衰减的稳定性;平均时间表示10次仿真实验中运算时间的平均值。
图1和图2显示了其他参数满足式(17)时,不同β值对算法性能的影响。从图1中可以看出,β≥1时,整体上阻带最大衰减、最小衰减及平均衰减都要好于β<1时的情形,表现出在相同条件下算法具有更好的性能。观察图2可以看出,β≥1时平均运算时间总体上要小于β<1时的情形,并且β≥1时其值越大,相应地平均运算时间也越大且有增加的趋势;当取值为整数时,平均运算时间相对较小。综上,本文推荐在能获得满足技术指标解的情况下,β取1~5之间的整数。
表1和表2显示了在根据仿真实验选取综合性能较好的组合α=1,β=2基础上,其他参数的配置是否满足式(17)对算法性能的影响。从表1可看出,此时阻带衰减情况比较理想,且阻带衰减方差波动较小,体现了算法良好的稳定性。表2中组1,6和8的阻带最小衰减相比滤波器系数取直接舍入解时性能要差,没有达到优化目的,说明此时算法失效;同时阻带衰减方差较大且有很大波动,表明此时算法非常不稳定。这说明式(17)对于参数的整体配置以及算法性能的提高有着积极的指导意义。
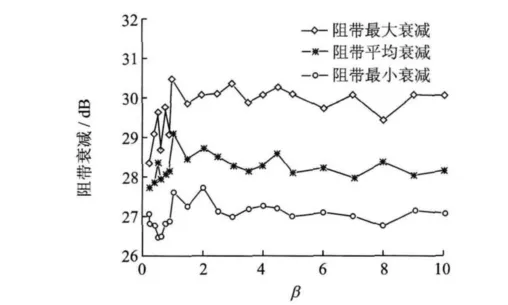
图1 参数β对阻带衰减的影响
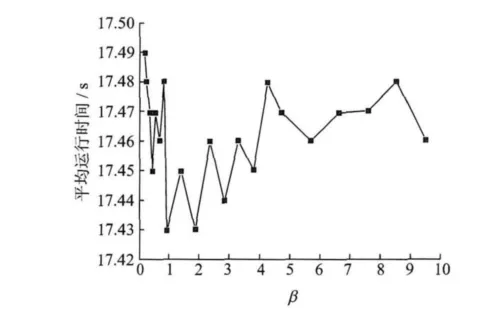
图2 参数β对运算时间的影响
近年来,一些研究将蚂蚁算法应用于自适应抗干扰天线[9]、FIR数字滤波器优化设计[12]等领域。这些应用研究中同样面临选择和配置蚂蚁算法参数的问题。参考文献[9]根据自适应信号处理原理和最小均方误差准则建立了数学模型,确定蚂蚁算法所要优化的目标函数。仿真实验中根据经验在自适应蚂蚁算法中参数选取为Q=40,ρ=0.9,τij(0)=1,α=3,β=1;文献[12]构造了一个优化窗函数的改进型蚂蚁算法,该算法将函数优化问题中生成解的过程转化为蚁群每前进一步就选择一个十进制数字并以此来生成一个十进制串的过程。仿真实验中有关参数取值为:Q=0.8,ρ=0.7,τij(0)=0.01,α=3,β=3。将文献[9,12]中选取的算法参数代入式(18)计算,结果相同。

表1 任意选取参数Q,ρ,τij(0)且满足式(17)
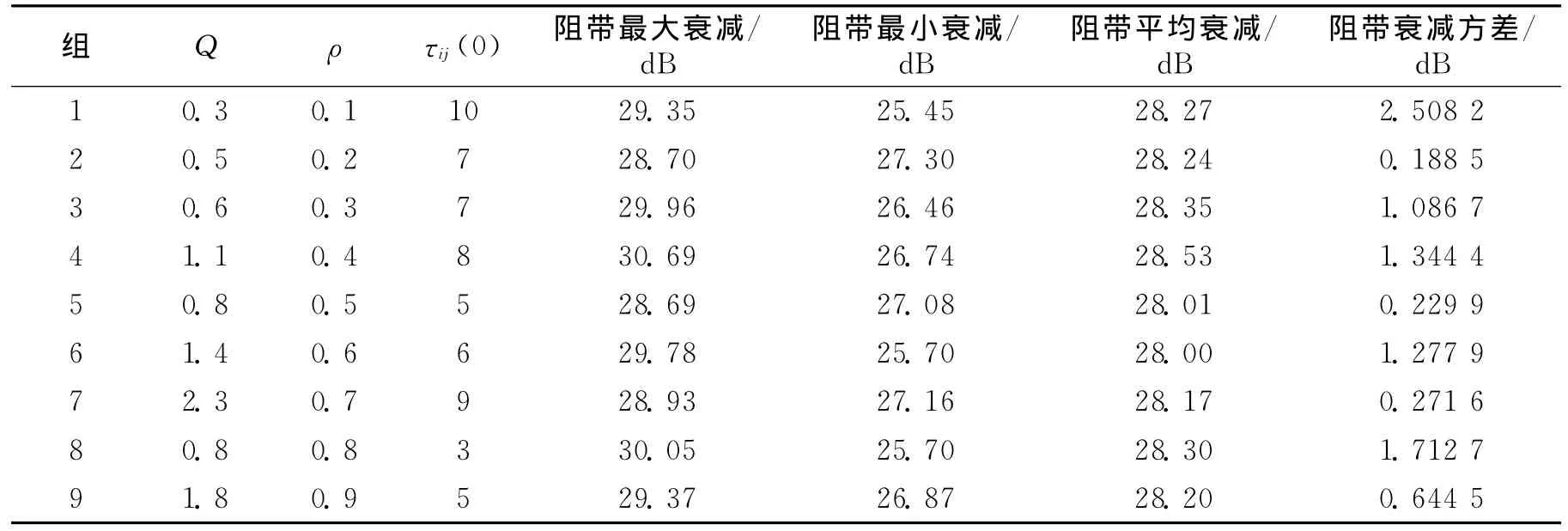
表2 任意选取参数Q,ρ,τij(0)且不满足式(17)
因为在蚂蚁算法中信息素强度的更新需要进行多步,例如在文献[9]中算法迭代了500次甚至2 000次,在文献[12]中,算法迭代次数达到了1 000次,所以从量级的角度考虑,可以认为式(19)成立。通过上述分析可以看出,虽然在不同的应用领域以及不同的优化准则下,sij的选取和定义有所不同,但是不同参数的选取同样一般地满足式(18)和式(17),结果吻合,说明本文提出的参数配置公式对于参数选择具有一定的指导意义。
4 结束语
本文在已完成的基于蚂蚁算法的FIR数字滤波器优化设计研究基础上,对优化设计中算法不同参数的作用、选取和影响进行了深入的分析和研究,简化了影响算法性能的参数个数。在理论分析的基础上,研究了相关参数的最佳配置,推导了参数配置的一般公式,在一系列仿真实验的基础上验证了本文的参数选取原则的有效性,同时还分析了蚂蚁算法在其他应用领域中的参数设置,经验证也满足本文所提出的参数选取原则,进一步表明本文的参数选取原则的可行性和有效性,为蚂蚁算法在优化问题中参数的科学配置提供了一定的参考。实验过程中发现受滤波器技术指标和优化准则的影响,选取的参数之间存在着较大的差异,波动性较大。如何改善和降低由滤波器技术指标和优化准则对参数设置带来的影响有待进一步深入的研究。
[1] Kodek D M.Design of optimal finite word length FIR digital filters using integer programming techniques[J].IEEE Trans Acoust,Speech,Signal Process,1980,28:304-308.
[2] Lim Y C,Parker S R.Discrete coefficient FIR digital filter design based upon an LMS criteria[J].IEEE Trans Circuits Syst,1983,CAS30:723-739.
[3] Jaumard M,Minoux M,Siohan P.Finite precision design of FIR digital filters using a convexity property [J].IEEE Trans Acoust,Speech,Signal,Process,1988,36:407-411.
[4] Cho N,Lee S U.Optimal design of finite precision FIR filters using linear programming with reduced constraints[J].IEEE Trans Signal Process,1998,46:195-199.
[5] Benvenuto B,Marchesi M.Digital filters design by simulated annealing[J].IEEE Trans Circuits Syst,1989,36:459-460.
[6] Gentili P,Piazza F,Uncini A.Efficient genetic algorithm design for power-of-two FIR filters,Proc[C]//IEEE Int Conf Acoust,Speech and Signal Prcocess.[S.l.]:IEEE,1995:1268-1271.
[7] Colorni A,Dorigo M,Maniczzo V.Distributed optimization by ant colonies[C]//Proc of ECAL91-European Conference on Artificial Life.Paris,France:[s.n.],1991:134-142.
[8] 谷鑫.基于有功功率平衡和蚁群算法优化PI参数的有源滤波器[D].天津:天津大学电气与自动化工程学院,2006.Gu Xin.Active power filter based on active power balance principle and ant colony algorithm optimized PI regulator[D].Tianjin:Electrical Engineering &Automation,Tianjin University,2006.
[9] 项建弘,郭黎利,王丽敏.基于复数蚁群算法的自适应抗干扰天线[J].数据采集与处理,2010,25(2):143-147.Xiang Jianhong,Guo Lili,Wang Limin.Adaptive anti-jam array antenna based on complex ant colony algorithm[J].Journal of Data Acquisition and Processing,2010,25(2):143-147.
[10]曹兰英,周晔,苏晓阳.一种用于SAR图像统计模型参数估计的蚁群算法[J].数据采集与处理,2009,24(1):78-81.Cao Lanying,Zhou Ye,Su Xiaoyang.ACA for statistical parameters estimation in SAR images[J].Journal of Data Acquisition and Processing,2009,24(1):78-81.
[11]仰继连,曾以成,徐茂林.设计有限字长FIR数字滤波器的蚂蚁算法[J].数据采集与处理,2009,24(3):375-379.Yang Jilian,Zeng Yicheng,Xu Maolin.Ant algorithm for designing finite wordlength FIR digital filters[J].Journal of Data Acquisition and Processing,2009,24(3):375-379.
[12]谢胜.蚁群算法在FIR数字滤波器设计中的应用[D].长春:吉林大学计算机科学与技术学院,2006.Xie Sheng.Ant colony algorithms for fir digital filters design [D].Changchun:College of Computer Science and Technology,Jilin University,2006.
[13]詹士昌,徐婕,吴俊.蚁群算法中有关算法参数的最优选择[J].科技通报,2003,19(5):381-386.Zhan Shichang,Xu Jie,Wu Jun.The optimal selection on the parameters of the ant colony algorithm[J].Bulletin of Science and Technology,2003,19(5):381-386.
[14]石立宝,郝晋.随机摄动蚁群算法的收敛性及其数值特性分析[J].系统仿真学报,2004,16(11):2421-2424.Shi Libao,Hao Jin.The numerical characteristics analysis and convergence proof for ant colony optimization algorithm with random perturbation behavior[J].Journal of System Simulation,2004,16(11):2421-2424.
[15]卢辉斌,贾兴伟,范庆辉.基本蚂蚁算法中参数的讨论与改进[J].计算机工程,2005,31(20):175-179.Lu Huibin,Jia Xingwei,Fan Qinghui.Discussion and improvement for parameters of ant algorithm[J].Computer Engineering,2005,31(20):175-179.
[16]吴春明,陈治,姜明.蚁群算法中系统初始化及系统参数的研究[J].电子学报,2006,34(8):1530-1533.Wu Chunming,Chen Zhi,Jiang Ming.The research on initialization of ants system and configuration of parameters for different TSP problems in ant algorithm[J].Acta Electronica Sinica,2006,34(8):1530-1533.
[17]刘刚,郭旭红,冯志华,等.蚁群算法在TSP中的仿真应用及最优参数选择研究[J].苏州大学学报:工科版,2007,27(1):56-59.Liu Gang,Guo Xuhong,Feng Zhihua,et al.Research on the optimal parameter selection of the ant colony system algorithm and its application in TSP[J].Journal of Soochow University:Engineering Science Edition,2007,27(1):56-59.
[18]章宝歌,杜呈欣.蚂蚁数和α、β的设置在求解函数优化中的影响[J].计算机工程与应用,2009,45(30):40-44.Zhang Baoge,Du Chengxin.Configuration of parametersα,βand ants′number for function optimization[J].Computer Engineering and Applications,2009,45(30):40-44.
[19]范小宁,林焰,纪卓尚.迭代更新蚁群管路敷设系统参数的敏感性分析[J].计算机工程,2007,33(15):36-39.Fan Xiaoning,Lin Yan,Ji Zhuoshang.Sensibility analysis of parameters in ACO for solving ship pipe routing[J].Computer Engineering,2007,33(15):36-39.
[20]张潇,王江晴.蚂蚁算法在带时间窗车辆路径问题中的应用及参数分析[J].计算机工程与科学,2010,32(12):134-136.Zhang Xiao,Wang Jiangqing.Application of the ant algorithm in the vehicle routing problem with time windows and its parameter analysis[J].Computer Engineering & Science,2010,32(12):134-136.

