基于语音压缩感知观测序列非重构的清浊音判别法
王文娟 杨 震
(1.南京邮电大学通信与信息工程学院,南京,210003;2.南京邮电大学宽带无线通信与传感技术教育部重点实验室,南京,210003)
引 言
根据语音信号是否有准周期性,可将语音分为浊音和清音,而清浊音的判别,是语音信号处理的关键部分,准确的清浊音判别,有助于提高提取基因周期的精确度、语音的识别与合成效果等。但目前各种清浊音判别的方法(短时能量、过零率、自相关函数)都是基于传统奈奎斯特采样,对噪声敏感,具有运算量大和复杂度高的缺点。而由Donoho等人提出的压缩感知理论(Compressive sensing,CS)[1-7]是近年来新兴的一种采样技术,该理论认为,如果信号在某个变换域上是稀疏的,就可以用一个与变换基不相关的观测矩阵将该信号投影到低维空间上,然后通过求解优化问题来高概率地重构原信号。同时压缩理论也指出,任何信号(包括语音信号)在找到相应的稀疏域的前提下都可以压缩,所以,只要能够找到或构建语音信号的稀疏基,就满足压缩感知理论的应用前提,然后可以对语音信号进行投影来得到样值个数很少的观测序列,根据这些较少观测序列所包含的信息同样可以重构原始语音信号[1-7],于是能够将压缩感知理论运用于语音信号处理中,构造基于压缩感知的语音处理系统,从而能够克服奈奎斯特频率采样带来的运算量大和复杂度高的缺点。国内外将CS理论运用到语音信号处理领域的研究也很多,但是鲜见针对获得的观察序列如何进一步提取语音特征参数的研究。文献[8]在语音识别中运用CS理论,能够很好地改善系统的抗噪性能;文献[5]将CS理论运用到语音编码进行有效编码;文献[9]提出了基于自相关观测矩阵的语音信号压缩感知。为了进一步深入研究CS理论在语音信号处理中的应用,清浊音的判别无疑是关键部分。
1 压缩感知基本原理
原始信号x=(x1,x2,…,xN)T可以用一组标准正交基Ψ=[φ1,φ2,…,φN]来表示,即
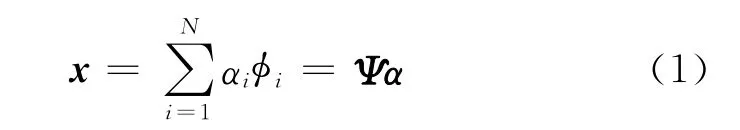
式中:α=[α1,α2,…,αN]T为原始信号x在正交基Ψ下的系数向量。严格来说,如果‖α‖0=K≪N,则 称x是K-稀 疏 的[4], ‖α‖p=为向量α中非零元素的个数。然后将这种在某正交基下具有K-稀疏性的信号投影到一个与正交基不相关的观测矩阵Φ上,得到观测向量
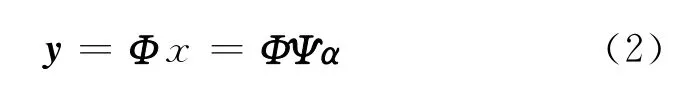
式中:观测矩阵Φ为M×N(M<N)矩阵,并且满足受限等距特性(Ristricted isometry property,RIP)[10]。由于M<N,式(2)为欠定方程组,不存在惟一解,但因为信号x在正交基Ψ下具有稀疏性,可以利用求解L0优化问题的方法来求解式(2)欠定方程组的问题

但求解式(3)非常困难,因信号具有稀疏性,式(3)的求解问题可以转化为L1优化问题求解[11],即
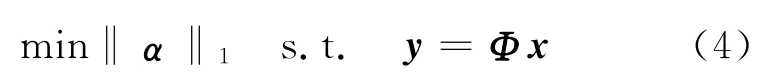
然后可通过基追踪[2]和正交匹配追踪[12]等算法来求解重构原始信号。
2 基于语音压缩感知的信号特征
语音在压缩感知领域的应用,大多是关于一些寻找最优稀疏基、观测矩阵和重构算法等方面,很少有涉及语音特性方面的研究,而此方面的研究又是语音信号处理领域中比较重要的环节。压缩感知理论的引用,使原始的奈奎斯特采样序列不能获取,取而代之的是语音压缩感知的观测序列,此观测序列与奈奎斯特采样序列有较大的区别。
本文实验过程中,采用的实验仿真环境如下:原始语音采样频率为16kHz;根据语音信号具有短时平稳性,将语音信号分帧处理,每帧长度为20 ms,共320个采样点;根据语音信号在DCT基(离散余弦基)上是近似稀疏的,研究中采用DCT基作为正交稀疏基,观测矩阵采用随机高斯矩阵[3]。本文后续研究的实验环境也同样设定。各取语音中清浊音20 000帧压缩感知序列的波形进行特征分析,每帧压缩感知观测序列的样值为80(即压缩比为1∶4),如图1所示。
由图1可以看出,浊音和清音压缩感知后观测序列的波形都类似白噪声,不再具有奈氏采样序列的特征,这无疑加大了语音信号特征提取的难度,如提取基音周期、清浊音判别等。所以根据目前的压缩感知理论,如果要提取原始语音的特性、沿用传统的奈奎斯特采样中提取语音信号特征的方法,必须将压缩采样得到的观测序列进行重构得到原始语音信号,而重构过程是一个计算量大、复杂度很高的问题,因而需要研究如何针对语音压缩感知的观测序列、在非重构的情况下,直接来提取语音的特性,为此本文给出了一种基于CS观测序列的能够区分清音和浊音的方法。
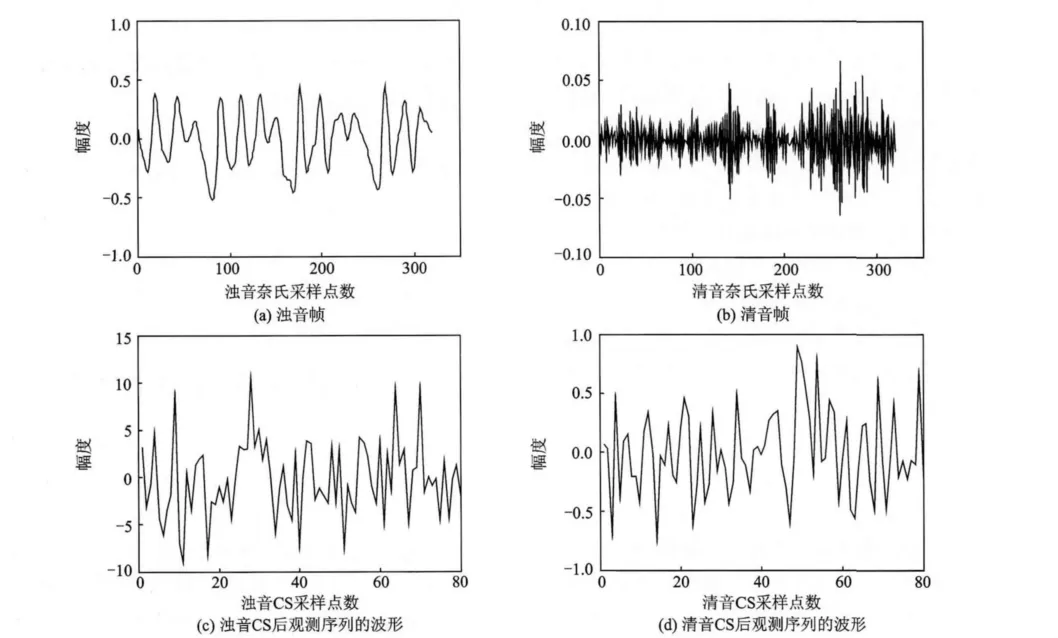
图1 清浊音帧和各自观测序列波形
3 基于语音压缩感知观测序列三阶累积量的清浊音判别及仿真
3.1 清浊音判别理论
根据语音产生的数字模型[13],语音分为清音和浊音,而图2所示数字模型可以近似模拟清音和浊音的产生,产生与发音器官相对应的信号序列,可利用此模型来近似分析语音的清音和浊音性质,故将语音分两部分来分析。

图2 语音产生的数字模型
(1)浊音:浊音是由准周期脉冲串激励产生,这一冲激串去激励一个系统函数G(z)(见式(5))[13]的线性系统,时域表达式见式(6)[13]
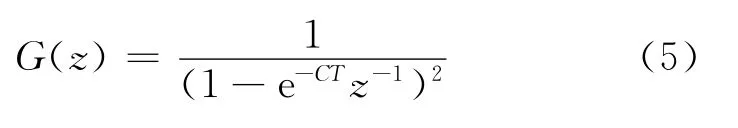

从G(z)系统输出的信号为正弦信号的变换,经幅度控制Av后输出的信号即为浊音激励,它是一个非高斯信号,这个非高斯信号经过一零极点数字声道模型V(z),由式(7,8)[13]可知,经过声道模型的输出仅仅是由uG(n)和uG(n)的延时信号的叠加,即输入到辐射模型R(z)的信号仍是一非高斯的信号,式(9)[13]说明R(z)是双线性变换,最后在模型右端得到的信号Pl(n)是非高斯信号。
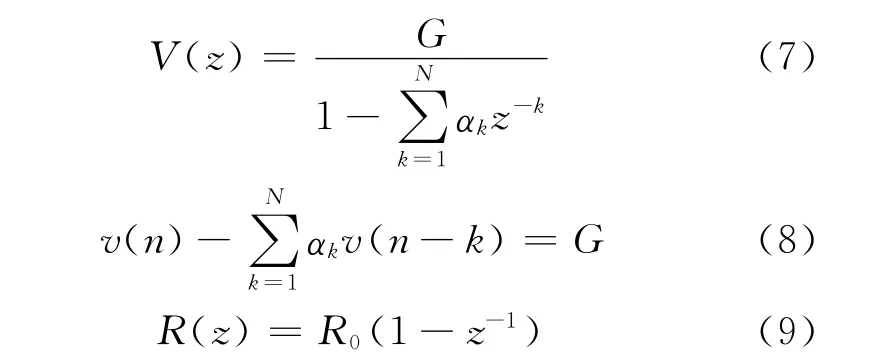
(2)清音:清音是由随机噪声激励产生,可以用均值为0,方差为1的高斯白噪声激励产生,经过幅度控制AN得到的是一个高斯信号,后经过声道模型线性系统V(z)和双线性辐射模型R(z),得到的Pl(n)信号是一个高斯信号。
综上分析,可以近似认为,对于语音信号而言,浊音是一个非高斯信号,清音是一个高斯信号。
压缩感知中,设定原始语音信号x=(x1,x2,…,xN)T,随机高斯矩阵
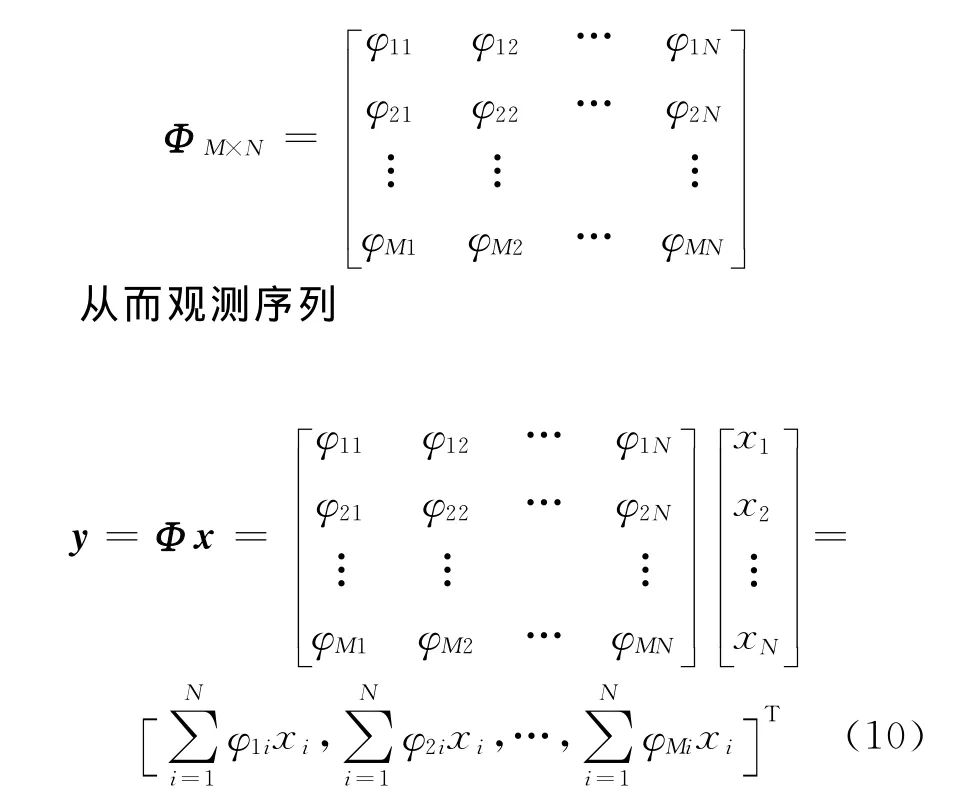
由式(10)可知,y(n)是由原始语音信号xi和高斯矩阵Φ相对行相乘求和所得,即观测序列y为原始语音信号的线性组合,所以对于浊音来说,非高斯信号的线性过程即观测序列仍是非高斯信号,而对清音而言,高斯信号的线性过程即观测序列仍是高斯信号。
原始信号经离散余弦变换(Discrete cosine transform,DCT)变换后再进行压缩感知,从而得到观测序列,根据式(2),观测序列也是由原始信号x与矩阵Φ相乘而得,基于上述理论,可以据此来设计新的直接从观察序列判断语音清浊音的方法。根据高阶累积量对零均值的高斯随机过程是“盲的”[14],即高斯过程三阶及三阶以上的累积量为0,所以对于压缩感知而言,观测序列近似高斯信号的清音的三阶累积量为0,而观测序列为非高斯信号的浊音的三阶累积量不为0,当然,现实中由于误差的存在,在仿真实验中,可以判别三阶累积量绝对值接近为0的帧为清音帧,这就是三阶累积量能够判别清浊音的理论基础。
3.2 清浊音判别仿真
本文仿真实验中采用标准数据库,实验采用本文第2节中的仿真环境,随机选取男声 “批评和自我批评”和女声 “大规模集成电路”为例,并将基于语音压缩感知观测序列三阶累积量的清浊音判别结果与传统的奈奎斯特采样中的能量判别准则相比较,判别结果中会出现某个野点,即在很多清音帧中间有一个浊音帧的出现,或是很多浊音帧中间有一个清音帧的出现,可以采用平滑的方法去除[15]。具体结果如图3,4所示,图中纵坐标“0”代表清音,“1”代表浊音。
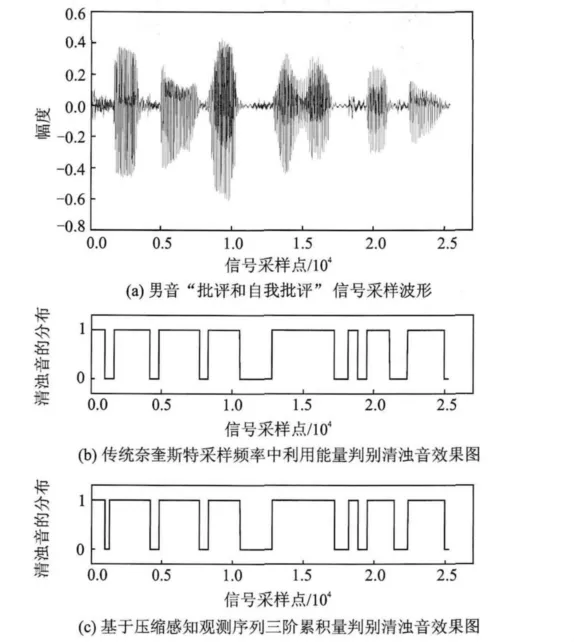
图3 直接基于观测序列的清浊音判别法与重构语音信号能量判别法相比较的结果
由图3,4可以看出,女声“大规模集成电路”共92帧,共11,50,73帧三帧判别结果不一致,而男声 “批评和自我批评”共79帧,只有5,67两帧的判别结果不一致,且这几帧还是处于清音和浊音分界之处的的混合帧,所以,基于压缩感知观测序列三阶累积量来判别清音和浊音的性能几乎可以与基于压缩感知重构语音信号的能量判别法相当。
现将本文提出的基于非重构、压缩感知观测序列三阶累积量的清浊音判别方法与基于压缩感知重构语音信号能量判别方法的运行时间做比较(压缩比为1∶4,每帧320个采样点),同一环境下,男音“批评与自我批评”的运行时间分别为264.83和548.66s,而女音“大规模集成电路”的仿真运行时间分别为289.55和618.06s,由此可以看出,在清浊音判别的准确度上,本文提出非重构情况下的清浊音判别方法与重构语音信号清浊音判别法几乎相当,但在运行时间上,可以缩短一半。
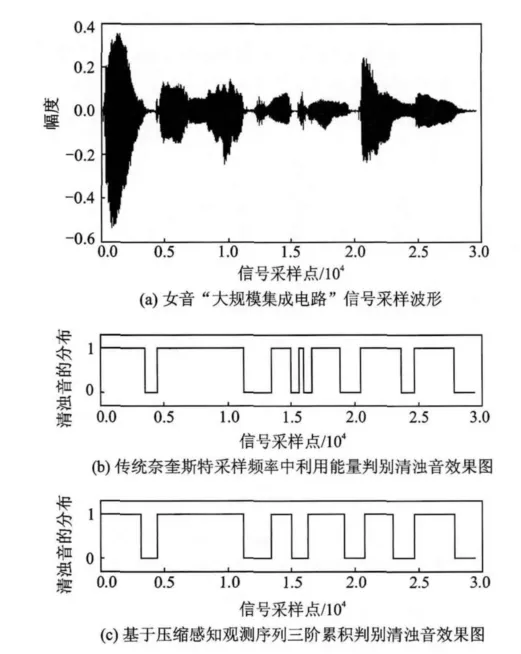
图4 直接基于观测序列的清浊音判别法与重构语音信号能量判别法相比较的结果
4 三阶累积量的清浊音判别方法对奈氏采样序列的适用性
基于三阶累积量的清浊音的判别准则对于奈氏采样序列同样具有适用性,据3.1节分析所知,对于语音信号而言,浊音是一个非高斯信号,清音是一个高斯信号,而高斯信号的三阶及三阶以上累积量为0,即清音的三阶累积量可以近似为0,浊音是非高斯信号,它的三阶累积量不为0,据此可以判别清音和浊音。
本文采用第2节的仿真环境,同样选取男声“批评和自我批评”和女声 “大规模集成电路”为例,并将基于奈氏采样序列的三阶累积量清浊音判别结果与奈氏采样序列中的能量判别准则相比较,具体结果如图5,6所示。
由图5,6分析,基于“原始语音信号的三阶累积量”能够判别清音和浊音,只不过门限的取值不同。女声 “大规模集成电路”共92帧,共50,77帧两帧判别结果不一致,而男声 “批评和自我批评”共79帧,只有26,67两帧的判别结果不一致,并且这几帧是混合帧,本身就不能完全判别为清音帧或浊音帧,所以这种判别方法对奈氏采样序列同样是适用的,只不过与传统奈氏采样序列中的能量判别法相比较,会增加运算量。

图5 基于奈氏采样序列三阶累积量清浊音判别法与能量判别法相比较的结果
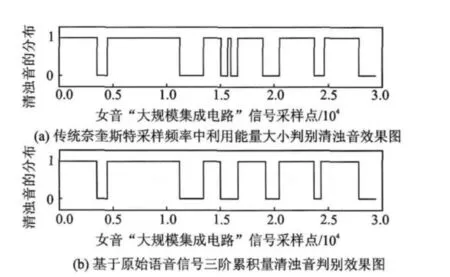
图6 基于奈氏采样序列三阶累积量清浊音判别法与能量判别法的比较结果
从另一个角度来看,语音信号是零均值、实的随机过程,而零均值的随机信号x(t)的三阶累积量的表达式[14]如下
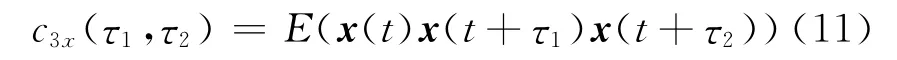
根据式(11),取τ1=τ2=0,则
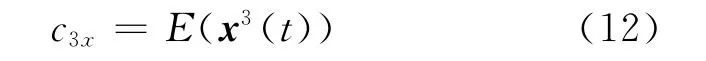
浊音的幅度大,清音的幅度小,由式(12),取三阶累积量的绝对值,浊音的三阶累积量也大于清音。所以,基于三阶累积量的清浊音的判别准则对奈氏采样序列同样具有适用性,不仅仅体现了“浊音是非高斯信号、清音是可以近似为高斯信号”的特点,还体现了原始语音“浊音幅度大,清音幅度小”的特点。
5 结束语
压缩感知技术具有广阔的应用领域,是信号处理领域的一次新的改革,将语音信号处理与压缩感知相结合,具有较高的研究价值,而清浊音的判别是语音信号处理中必不可少的环节,针对这种情况,本文提出了一种基于压缩感知观测序列的清浊音判别方法,它的判别性能好,为压缩感知理论在语音信号处理中的应用提供了研究基础。
[1] Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[2] Candès E,Romberg J,Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2006,52(2):489-509.
[3] Baraniuk R G.Compressing sensing[J].IEEE Signal Processing Magazine,2007,24(4):118-121.
[4] 石光明.压缩感知理论及研究进展[J].电子学报,2009,37(5):1070-1081.Shi Guangming.Advances in theory and application of compressed sensing[J].Chinese Journal of Electronics,2009,37(5):1070-1081(in Chinese)
[5] Giacobello D,Christensen M G,Murthi M N,et al.Retrieving sparse patterns using a compressed sensing framework:applications to speech coding based on sparse linear prediction[J].Signal Processing Letters,2010,17(1):103-106.
[6] PeyrèG.Best basis compressed sensing[J].IEEE Transactions on Signal Processing,2010,58 (5):2613-2622.
[7] Candès E,Tao T.Near optimal signal recovery from random projections:universal encoding strategies[J].IEEE Transactions on Information Theory,2006,52(12):5406-5425.
[8] Gemmeke J F,Cranen B.Using sparse representations for missing data imputation in noise robust speech recognition[C]∥European Signal Processing Conf(EUSIPCO).Lausanne,Switzerland:[s.n.],2008:787-791.
[9] 季云云,杨震.基于自相关观测的语音信号压缩感知[J].信号处理,2011,21(2):207-212.Ji Yunyun,Yang Zhen.Compressed speech signal sensing based on auto-correlative measurement[J].Signal Processing,2011,21(2):207-212.
[10]Ying L,Zou Y M.Linear transformations and restricted isometry property[C]∥IEEE International Conference on Acoustic,Speech and Signal Processing.Taipei,China:[s.n.],2009:2961-2964.
[11]Donoho D L,Huo X M.Uncertainty principles and ideal atomic decomposition[J].IEEE Trans on Information Theory,2001,47(7):2845-2862.
[12]Pati Y C,Razaiifar R,Krishnaprasad P S.Orthogonal matching pursuit:recursive function approximation with applications to wavelet decomposition[C]∥The 27th Asilomar Conference on Signals,Systems and Computers.Pacific Grove,USA:[s.n.],1993:40-44.
[13]王炳锡.语音编码[M].西安:西安电子科技大学出版社,1999.Wang Bingxi.Speech coding[M].Xi′an:Xidian University Press,1999.
[14]张贤达.现代信号处理[M].北京:清华大学出版社,2002.Zhang Xianda.Modern signal processing[M].Beijing:Tsinghua University Press,2002.
[15]李振起,姜占才,李大筠.一种清浊音判决的参考标准及一种新算法[J].电脑开发与应用,2010,23(12):9-12.Li Zhenqi,Jiang Zhancai,Li Dajun.A kind of reference standard for UV decision and a new algorithm[J].Computer Development and Application,2010,23(12):9-12.
——以NHK新闻为中心

