由10个函数图线全面理解“闭合电路”中的规律
郭振勇
(浙江省温州中学,浙江 温州 325014)
“闭合电路的欧姆定律”是“恒定电流”一章的灵魂部分,也是整个高中阶段的重点内容,是电学实验的理论基础,是会考及高考中的必考知识点.通过对它的考查,可以反映学生的综合分析问题的能力、处理实验数据的能力、利用图像解决物理问题的能力.笔者总结出了10个函数图线,现通过如图1的电路加以分析说明.其中R1为定值电阻,R2为滑动变阻器,外电阻用R表示(R=R1+R2);所有电表均为理想的,其示数分别用I、U、U1、U2表示;电源电动热势为E,内阻为r.

图1
1 电压与电流间的函数图线
(1)路端电压U与干路电流I间的函数图线(如图2).

图2
斜率的数值为电源内阻,纵截距为电源电动势,横截距为电源短路电流.
(2)定值电阻的电压U1与其电流I间的函数图线如图3.

图3
斜率的数值为定值电阻阻值.
(3)可变电阻的电压U2与其电流I间的函数图线如图4.
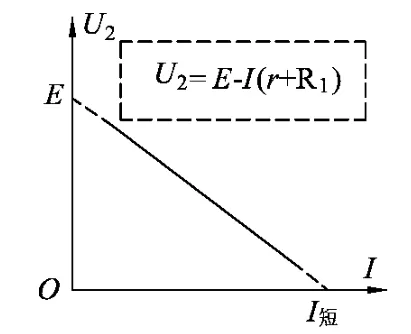
图4
斜率为电源内阻与R1之和,纵截距为电源电动势,横截距为电源短路电流.
说明:① 对第(3)种情况,有些学生用“U2=I R2”来处理是不恰当的,因该式中的3个物理量都是变化的,不易画出其间的函数图线.
②“三合一”:将3个图线画在同一坐标系下,更能直观地反映出其间的关系如图5.a点的意义:U1=U,此时R2=0.
b点的意义:U1=U,此时R2=R1.

图5
2 电流、电压与外电阻间的函数图线
(1)干路电流I与外电阻R(R=R1+R2)间的函数图线及其变换图形(如图6、图7).

图6

图7
(2)路端电压U与外电阻R(R=R1+R2)间的函数图线及其变换图形(如图8,图9).

图8

图9
说明:将曲线转换成直线,更容易反映出各物理量间的变化规律.这是物理学中研究问题,探寻规律时常用的方法.
3 电源的输出功率与外电阻、电流、电压间的函数图线(如图10-12)

② 此处的3条曲线均不易转成直线,因关系式里面同时含有自变量的一次项和二次项.
4 图线应用举例
例1.甲学生设计了如图13所示的电路测电源电动势E及电阻R1和R2的阻值.实验器材有:待测电源E(不计内阻);待测电阻R1,待测电阻R2;电压表V(量程为1.5V,内阻很大);电阻箱R(0~99.99Ω);单刀单掷开关S1;单刀双掷开关S2;导线若干.
(1)先测电阻R1的阻值.请将甲同学的操作补充完整:闭合S1,将S2切换到a,调节电阻箱,读出其示数r和对应的电压表示数Ul,保持电阻箱示数不变,______,读出电压表的示数U2.则电阻R1的表达式为R1=________.


图13

图14
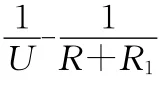

比较(1)、(2)两式可知,在R 取值一样的情况下,S2切换于b时电压表的值比S2切换于a时要大,但电压U的最大值不变,而最小值变大,故S2切于b时电压表示数变化范围小,造成图线描绘不准.
例2.有3个电源:甲(电动势为2V、内阻为3Ω)、乙(电动势为2V、内阻为2Ω)、丙(电动势为2V、内阻为1Ω),定值电阻R=2Ω.在R的两端接入哪一个电源,可使该电源的输出功率最大?
解析:当外电阻可变时,电源输出功率是非单调变化的,R=r时电源输出功率最大.当外电阻不变时,电源输出功率可由P=I2R求解,P随I单调变化,当r最小时I最大,P最大.所以,在R的两端接入丙电源,可使其输出功率最大.

