方向舵静强度试验载荷等效计算研究
(中国民航大学航空工程学院,天津 3 00300)
在飞机结构,尤其是飞机翼面结构的静强度试验中,外载荷施加的真实程度是分析成败的前提条件之一,即施加于加载点上的外加载荷尤其是气动载荷的真实程度是一个非常关键的因素,而加载点处的载荷一般是由翼面结构所承受的气动分布载荷依据一定的数学算法和力学原理等效得到的[1]。这里的载荷等效方法要基于静力等效原则,即总压心及总载荷不变,以保证等效后载荷的真实性和可靠性[2]。飞机的翼面承受的为气动力分布载荷,在静力试验之前要先转化为气动网点的离散载荷。翼面结构上的气动网格一般是展向和弦向的等百分线相交形成的网格群[3]。
1 气动载荷
作用于翼面结构的气动载荷为一种分布式的表面力,通常要通过空气动力学及飞行力学的有关分析、实验来确定其分布以及大小[4]。
气动力网点上的气动力载荷信息包括如下内容:
(1)气动力网格上的气动力载荷分布;
(2)载荷设计情况以及相应的飞机状态参数(包括Ma数、飞行高度、飞机过载等);
(3)气动力网点坐标,加载点坐标以及对应的坐标系。
翼面结构的有限元分析要遵循静力等效原则,在应用这一原则时应保证载荷传递路线的正确性,如不可跨越重要的传力部件,以保证结果的准确性[5]。
2 载荷等效计算方法
载荷等效计算方法主要遵循静力等效原则和传力路线不变的原则。静力等效原则保证了总载荷和总压心不变,而传力路线不变主要体现在保证载荷的真实传递,特别是在相邻部件交接区,如翼面与舵面之间[6]。
该载荷等效计算方法,根据静力等效原则,基本思路是:离气动点近的有限元节点多分配一些,反之少分配一些。
对于一块气动网格o(xo,zo)上的气动载荷,其上载荷为po。假设预先布置好的所有加载点 {(xk,zk),k=1,2,3,…,n}与该气动力网点o之间存在一个虚拟的梁(长度为lk),它们都是以o点一端为固支的悬臂梁,如图1所示。则加载点分配到载荷pk时的变形能为:

式中,
EJ为虚梁元的抗弯刚度,于是整个系统的变形能为:

分配到加载点上的载荷,应使系统的变形能最小,而且满足静力等效条件即:
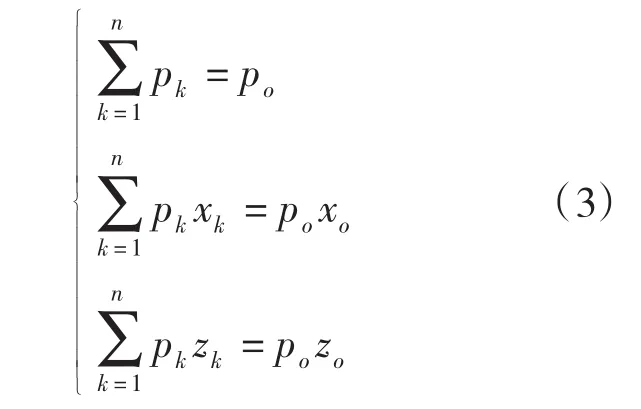
其中,
k为加载点的数目。
用拉格朗日乘子法建立拉格朗日函数:

式中,
λ、λx、λz为拉格朗日乘子且有:
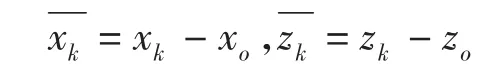
为使F(λ、λx、λz)取最小值,令

并令3EJ=1可得:

上式中:k=1,2,3,…,n
代入静力等效条件(3),最后得:
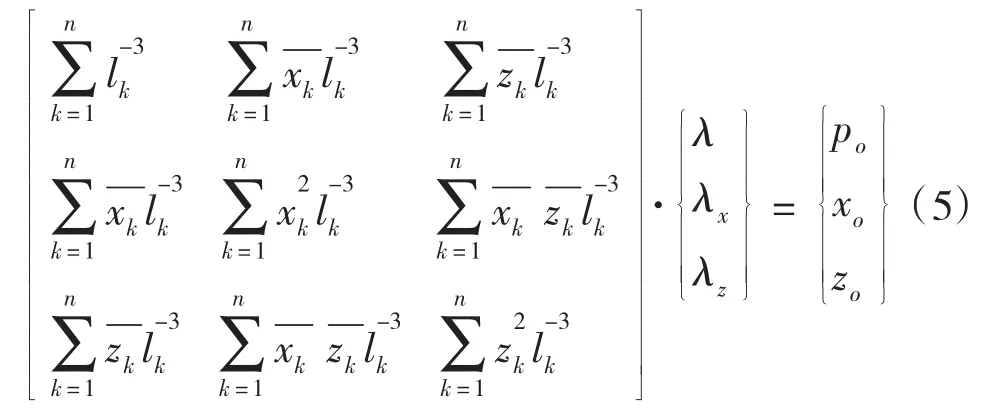
通过以上矩阵运算可以解得 λ、λx、λz,回代(4),即可得到一个气动力网点上的载荷:
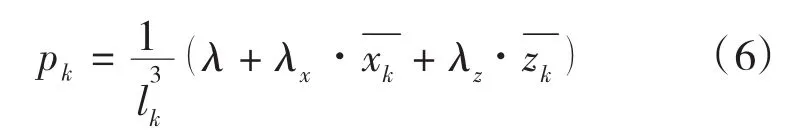
用相同的方法解得其它每个气动网点等效到各个加载点上的载荷,再将同一个加载点上得到的载荷叠加,即可得到翼面气动分布载荷等效到加载点上的载荷。
这种计算方法,统筹考虑了所有气动力网点和所有预先布置的加载点,可以根据实际载荷情况布置加载点的位置,算法实现简单,容易编制计算机程序进行自动计算。
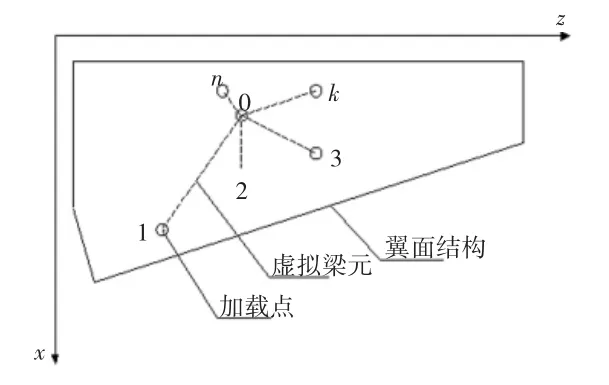
图1 单个气动网点载荷向多个加载点转换示意图
3 载荷等效软件编写及应用
考虑到Matlab具有强大和高效的矩阵运算功能,同时能够利用GUI编写较好的人机交互界面,故选用Matlab作为编写程序的核心软件。图2为GUI人机界面,在界面中输入方向舵展向和弦向分段数m和n,即分别将方向舵在展向和弦向长度上平均分为m份和n份,确定网格种子,其气动网格同时被确定,如图 3(此算例中 m=6,n=4)。
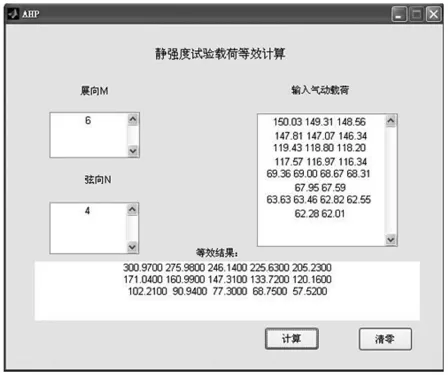
图2 静强度试验等效载荷计算软件界面
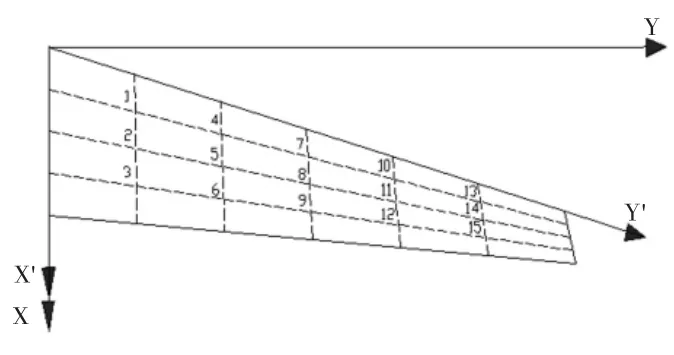
图3 某飞机方向舵的气动网格
图中有两个坐标系X-Y和X’-Y’,X-Y为一般直角坐标系,X’-Y’为沿方向舵两条边在展向和弦向的非直角坐标系。在GUI人机界面中输入m和n的数值后,在程序中利用插值运算,可以计算出图中各个节点在X’-Y’坐标系中的坐标。在方向舵的工业图纸中测量得到Y轴和Y’的夹角为38°,由三角转换关系可以将X’-Y’非直角坐标系中的坐标转换为X-Y直角坐标系中的坐标以便于程序下一步的计算。
表1和表2分别为经过坐标转换计算后气动载荷压心和加载点在X-Y直角坐标系中的坐标。其数值是在程序计算过程中产生的结果,不会在软件界面中显示。

表1 转换后的气动载荷块压心坐标(mm)

表2 转换后的加载点坐标(mm)
表3为方向舵舵面的气动载荷分布。其数值是参考飞机设计手册第九册第1篇第2章飞机载荷计算,在偏航机动舵偏贡献情况下计算方向舵对垂尾载荷计算得来,其舵偏角为最大偏转角度30°。计算过程中的气动参数参考飞机设计手册第六册气动设计得来[8]。气动载荷计算完毕后,将其数值按照图3中气动块的分布形式,以矩阵形式输入到GUI界面中气动载荷相应栏中。

表3 方向舵气动载荷分布(N)
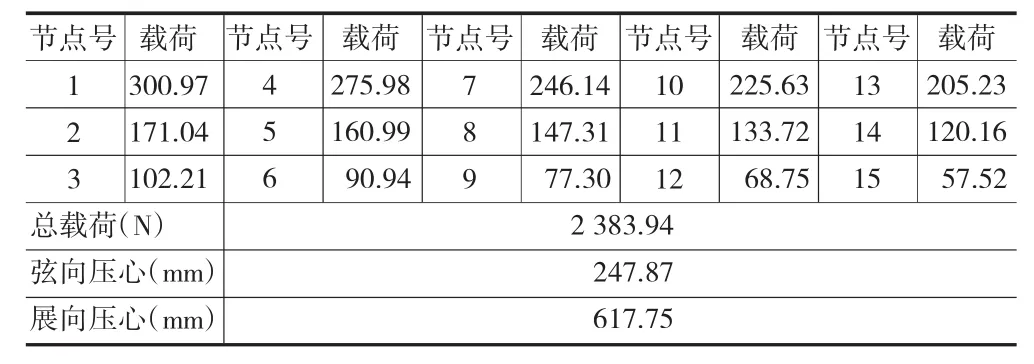
表4 计算后方向舵加载点载荷(N)
数值输入完毕后,点击计算,程序即开始运行,其运行步骤如下:
(1)计算气动载荷压心和节点坐标并进行转换,得到表1和表2中的结果;
(2)提取表2中每一对相对应的X值和Y值与表1中1个气动载荷坐标来计算虚拟梁的长度lk和对应的;
(3)将lk带入式(5)左边的矩阵中,计算矩阵中的每一个元素;
(4)从表3中提取步骤2中气动载荷块的载荷和坐标,带入式(5)中右边矩阵中;
(5)进行矩阵运算,计算出式(5)中中间矩阵元素值,即拉格朗日乘子的值;
(7)以上步骤4到步骤6循环计算,把每一个气动载荷块的载荷等效到所有加载点上,最后每个加载点上的载荷叠加即可得到结果。其结果将在GUI界面中等效结果一栏显示。
由于方向舵的气动载荷在弦向上变化很大,将表3中方向舵的每一块气动载荷沿弦向叠加,可得到方向舵气动载荷的弦向分布。同样,将表4中每一点的加载点载荷沿弦向叠加,可得到方向舵节点载荷的弦向分布[9],其结果见图4。其总载荷分别为2 384.06 N和2 383.94 N,其弦向压心和展向压心计算前后分别为(248.34,619.65)和(247.87,617.75),其计算前后误差很小。同时,气动载荷和节点载荷在方向舵弦向上的变化趋势如图4所示,其变化趋势一致。此外,图5为飞机设计手册第9册中舵偏贡献下垂尾载荷的弦向分布,图中铰链轴右侧部分为方向舵的弦向载荷分布情况,其气动载荷的弦向分布趋势也是一致的。

图4 气动载荷和节点载荷弦向分布对比

图5 垂尾载荷弦向分布[7]
4 结束语
本文介绍的方法在理论上依据充分,通过算法实例证明,在计算数据和曲线分布两方面综合考虑,计算的结果可靠,计算结果误差可以接受,适用于一般飞机结构静强度实验。根据这种方法编写的载荷计算程序,可执行性强,程序结构清晰明确,在方向舵或翼面结构的有限元分析中,可以节省原始数据的准备时间,实用性较高,可应用于教学及实践中。但是,发展更精确的载荷计算方法和等效方法,进一步丰富所编写软件的内容和扩大其适用范围将是下一步的研究目标。
[1]陈全礼,熊建琦,杨剑锋.飞机结构静强度试验载荷等效方法应用[J].飞机工程,2005,(1):63-65.
[2]王专利.翼面结构有限元模型节点气动载荷计算[J].洪都科技,2007,(1):7-10.
[3]邹群飞.机身气动载荷计算[J].洪都科技,2009,(4):9-14.
[4]Daniel P.Raymer,Aircraft Design:A Conceptual Approach Third Edition,American Institute of Aeronautics and Astronautic[J].Inc,1999,(5):28-31.
[5]邵长林,吉桂兴.ARJ21复合材料方向舵设计[D].江苏:南京航空航天大学,2004.
[6]《飞机设计手册》总编委会.飞机设计手册第9册载荷、强度和刚度[M].北京:航空工业出版社,2001.
[7]《飞机设计手册》总编委会.飞机设计手册第6册气动设计[M].北京:航空工业出版社,2002.
[8]叶天麒,周天孝.航空结构有限元分析指南[M].北京:航空工业出版社,1996.

