通信网络中带有Markov 故障流的MAP/M/∞排队模型①

周宗好， 朱翼隽， 石志岩

(1.黄山学院数学与统计学院，安徽 黄山245041;2.江苏大学理学院，江苏 镇江212013)

0 引 言

在现代通信网络中，一种有效的建模方式就是假设信息到达为马尔科夫过程，能够很好的描述到达过程的突发性和周期性，它包括了泊松过程、PH更新过程及调制的泊松过程(Markov Modulated Poisson Process，MMPP)等［1-2］.

在经典的排队系统中总是假设服务台不会发生故障的，这显然不符合现实的. 实际上服务台总是受一些不可预测的因素影响而发生故障不能工作，例如在通信网络中，信号的中断、线路损坏等因素都导致信道不可用，都称之为故障. 因此，文献［3，4］研究了M/G/1 可修排队系统，并且朱翼隽等［5］带重试策略的可修排队系统的详细的可靠性指标.但是故障的到达类似于系统信息流的到达一样，到达过程不是泊松流能精确描述的，而上面提到的文献都是假设故障到达间隔时间分布是指数分布.因此，对带有马尔科夫故障流与泊松故障流排队系统的性能比较研究显得具有重要的意义了.

对于可修系统的维护策略已经被广泛的研究［6～7］，例如有故障修理、元件替换和定期维修等，但是对于通信系统来说，为了维持通信的即时性和服务质量，采用备用一定数量的服务台替换因故障不能工作的服务台是提高服务质量提高效率的重要方法.因此本文中我们考虑服务台数量为无限的数据包到达是Markov 流的排队模型.

1 模型描述

考虑数据包到达流为Markov 流，服务台对信息服务时间为指数分布的MAP/M/c 可修排队系统，系统有k 个等待位置的缓冲器且故障到达为Markov 流，c 个服务台处于工作状态，备用服务台数目为无限.当工作状态的服务台一旦发生故障，则备用的服务台立即替代工作，发生故障的服务台进入等待修理的队列，按先到先服务规则等待修理，并且假定系统只有一个修理工. 服务台的故障到达流为马尔科夫过程MAP1，它的有J1× J1维隐马尔科夫链J1(t)、矩阵表示(C0，C1)、生成元矩阵C(1)= C0+ C1以及1 × J1维的稳态概率向量θ1和到达率分别为λ1= θ1C(1)eJ1.

数据包的到达流为马尔科夫过程MAP2，它的有J2× J2维隐马尔科夫链J2(t)、矩阵表示(D0，D1)、生成元矩阵D(1)= D0+ D1以及1 × J2维的稳态概率向量θ2和到达率λ2= θ2D(1)eJ2.到达的数据包如果发现在岗的个服务台全部被占则进入缓冲器，如果缓冲器的位置也全部被占，则其离开系统，即数据包丢失. 数据包的服务时间和服务台的修理时间分别服从参数为μ1和μ2的指数分布.故障的到达过程MAP1、数据包的到达过程MAP2、数据包的服务时间及服务修理时间是相互独立的.

2 生成元矩阵

马尔科夫过程ζ(t)= {X1(t)，X2(t)，J1(t)，J2(t)}的状态空间为:

按字典序排列马尔科夫链{ζt，t ≥0}的状态空间S的元素，可得其生成元矩阵Q 具有QBD 结构为:

这里的矩阵块A0，A，B，C 分别为:

把上面方程(1)～(3)按k = 0，1，…，K 相加，得到:

又因为C(1)⊕D(1)不变向量的唯一性和πe =1，可以得到:

因此可以得到下列定理:

定理1 具有生成元矩阵Q 的马尔科夫过程{ζt，t ≥0}是正常返的充要条件是:ρ = λ1/μ1＜1.证明: 因为马尔科夫过程{ζt，t ≥0}的生成元矩阵具有QBD 结构，由文献［8］知道它的正常返的充要条件是πCeJ1J2＜πBeJ1J2，因此我们计算得:

设在稳态条件下，具有生成元矩阵Q 系统的稳态概率向量为¯且，因此我们可以得到下列定理:

定理2 马尔科夫过程{ζt，t ≥0}存在唯一的稳态概率向量¯x 满足¯xQ2= 0，¯xe∞= 1.其元素为:

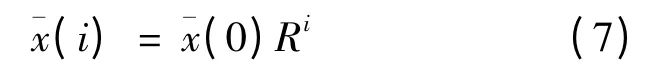
其中，向量x(0)由下列矩阵方程给出:

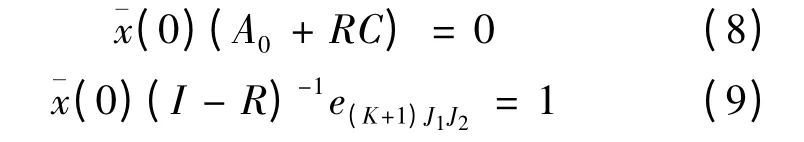
这里的率阵R 是矩阵方程R2B+RA+C = 0 的最小非负解，它的谱半径SP(R)＜1，由文献［8］知道R 是矩阵序列{R(n)，n ≥0}的极限= R，其中矩阵序列的按下列方法确定的:

率阵 R 的迭代计算直到满足不等式maxi，j［Ri，j(n + 1)- Ri，j(n)］ ＜ ε 为 止. 这 里Ri，j(n)是矩阵R(n)第i 行、第j 列的元素，ε 为迭代计算的精度.

3 系统排队指标

系统中恰有k 个数据包在等待服务的概率为:

系统中等待服务数据包的平均对长为:

4 服务台的可靠性指标

服务台的可用度:

服务台的故障频度:

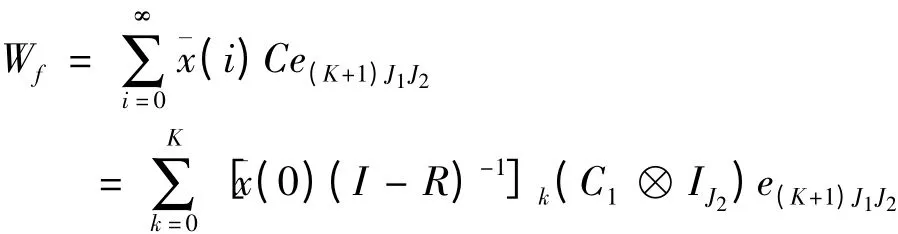
系统中等待修理的服务台的平均对长为:

5 数值例子

在本节用两个例子来计算模型的服务台的可靠度和故障频度，主要是为了说明备用服务台数目对系统指标的影响.

例1 设μ1= μ2= 1，2.马尔科夫过程MAP2定义为:

先引入马尔科夫过程MAP2的相关系数ccor的概念［2］:

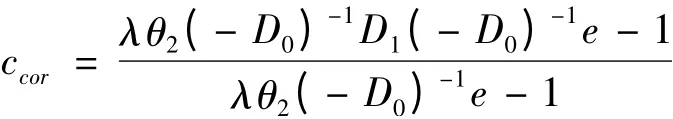
由此可以计算得到上面的马尔科夫过程MAP2的相关系数ccor= 0.05，并且记为MAP2(0.05).马尔科夫过程MAP1被定义为MAP1(0.06)，其形式如下:

从表1 中，我们可以看出模型的稳态概率向量¯x(i，k)随等待位置K 的变化情况，从数据上可以看出稳态条件下，系统的概率向量¯x(i，k)受等待位置K 的变影响较小.

例2 在这个例子中，马尔科夫过程MAP2被定义为MAP2(0.1)，其矩阵表示为:

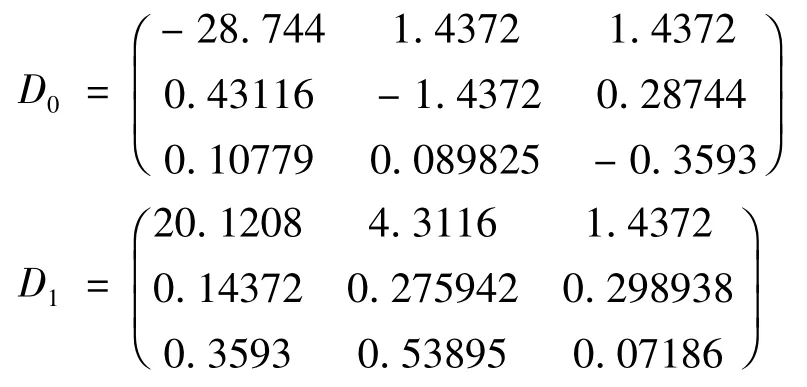
马尔科夫过程MAP1分别用下列五个到达过程表示:

1.指数分布(EXP):C0= ¯c(-1);C1= ¯c(1)

2. 超指数分布(HEX):

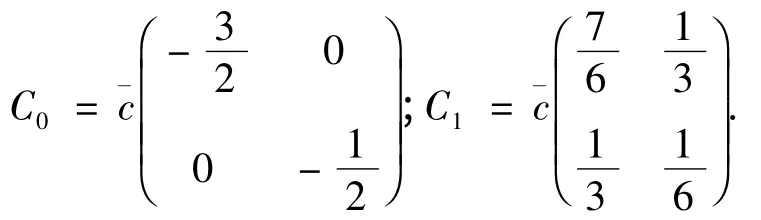
3. 爱尔朗分布(ERL):

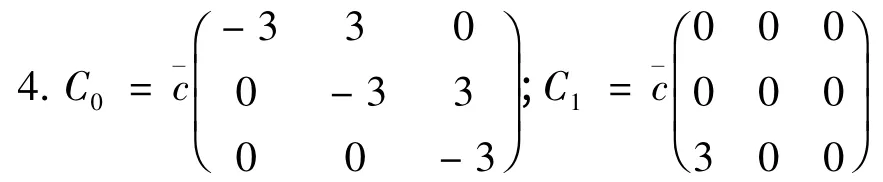
表1 当μ1 = μ2 = 1.2 时，x(i，k)的值

5. MAP1(0.2):

图1 故障流到达率λ1 与平均队长E［N1］与关系图

图1是反映模型的性能指标随故障流的基础到达率λ1的变化情况，我们可以得到下列重要的结论:模型性能指标(数据包的受阻率Pb、数据包的平均队长E［N2］和故障服务台的平均队长E［N1］)随故障流的基础到达率λ1的增加而迅速增加;进一步可以看出，不同的到达流对这些指标的影响也是非常大的，其中，爱尔朗到达流引起的数据包拥塞最小，而相关系数越大的马尔科夫流引起的数据包拥塞越大.

6 结 论

考虑到随着通信网络的发展，网络中的数据包(包括语音呼叫、文字信息、图片等数据业务)往往具有爆发性和周期性，用传统的泊松流是不能完全的刻画网络信息流的特性.本文采用马尔科夫数据包到达流和故障到达流替代传统的泊松流，通过比较分析发现两者对系统性能指标影响差距很大，因此，本模型为建立更精确的排队模型提供一定理论依据.

［1］ W. Joris，S. Bart，B. Herwing.Performance Analysis of a Single ATM Queue with a Priority Scheduling［J］.Computer ＆ Operational Research，2003，30 (12):1807 -1829.

［2］ J. R. Artalejo，S. R. Chakravarthy. Computational Analysis of the Maximal Queue Length in the MAP/M/c Retrial Queue［J］.Applied Mathematics and Computation，2006，183(2):1399 -1409.

［3］ C. Gautam，T. Lotfi.An M/G/1 Queue with Two Phases of Service Subject to the Server Breakdown and Delayed Repair［J］. Applied Mathematical Modelling，2009，33 (6):2699 -2709.

［4］ A. B. Khalid，D. Alexander，K. Arseniy，Y. Suleimen.Investigation of the M2/G2/2/∞N Queue with Restricted Admission of Priority Customers and its Application to HSDPA Mobile Systems［J］.Computer Networks，2009，53(8):1186 -1201.

［5］ 朱翼隽，周宗好，冯艳刚.具有优先权的M/G/1 重试可修排队系统［J］.自动化学报，2008 34:195 -201.

［6］ Z. M. Liu，J. B. Wu，G. Yang.An M/G/1 Retrial G-queue with Preemptive Resume and Feedback under N -policy Subject to the Server Breakdowns and Repairs［J］. Computers ＆ Mathematics with Applications，2009，58(9):1792 -1807.

［7］ P. O. Rafaek，M. C. Delia. A Multiple System Governed by a Quasi-birth - and - death Process［J］. Reliability Engineering and System Safety，2004，84 (2):187 -196.

［8］ M. F. Neuts. Matrix - geometric Solutions inStochastic Models［M］. Baltimore:The Johns Hopkins University Press，1981:1-40.