关注差异 灵动课堂——以“异分母分数加减法”为例

饶道松

（南京师范大学附中仙林学校小学部，江苏 南京 210046）

关注差异 灵动课堂
——以“异分母分数加减法”为例

饶道松

（南京师范大学附中仙林学校小学部，江苏 南京 210046）

一、前置性思考

一思：你如何解决这个问题？请把你思考的过程呈现出来。

二思：还有别的方法解决吗？如果有，请写下来。

三思：（如果有二思的话）比较这几种解决方法，你有什么想法？

一思：请用你认为最合适的方法尝试解决这个问题。

二思：为什么你首选用上面的这种方法去解决问题？

三思：观察问题一、问题二的解决过程，你觉得计算异分母分数加、减法应怎样计算？需要注意什么？

二、课堂展示交流

（一）交流前置性思考中的“问题一”

师：昨天下发了导学稿，布置大家就两个问题进行独立的思考。我们先看第一个问题，能用两种以上方法来解决这道题的同学请举手。

大约有23的学生举手，老师让孩子们在4人小组内交流各自的思考。

师：哪个小组愿意到讲台前汇报你们组的想法？

组员1：我利用画图的方法，（利用实物展示台），因为

组员2：可以把这两个分数都转化成小数进行计算。

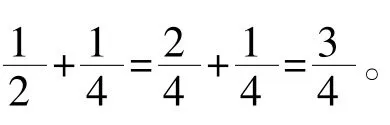
生2：我来补充一下：如1元+1角，这个就不能直接相加，因为的它们的单位名称不一样，分数相加也是同样的道理。

生3：是的，整数、小数相加减也要相同的数位对齐，为的就是相同计数单位的数才能相加。例如1.3+7中，3不能和7相加，因为“3”的计数单位是0.1，而7的计数单位是1。

师：他的解释你满意吗？

生：满意。

师：刚才我们讨论汇报了一共有3种解决方法。让我们来比较一下，你从中发现了什么？

生：我发现这三种方法有一个共同点：都是把异分母分数转化成我们已经学过的知识然后再进行运算的。

师：像这种把没有学过的知识转化成已经学过的知识进行运算，其实就是一种转化的策略，转化的思想。让我们再回顾一下这三种方法，虽然解决的过程不同，但是有一个共同点是——

生：都有一个共同点是把单位统一了。画图法，将两个异分母分数通过图形转化成分数单位相同的；转化成小数加法就是让相同计数单位的数进行相加；通分后再计算更是将它们的分数单位统一了。

师：看来，不同的方法之间是有共通之处的，那就是，它们的解决办法中都用到了转化，都做到了单位统一。

（二）交流前置性思考中的“问题二”

师：掌握了这么多解决问题的办法，解决第二个问题和第一个问题的要求就不一样了，希望你采用的是最合适的方法。谁来和大家交流一下？

师：对于她的回答，还有什么意见或者需要补充的吗？

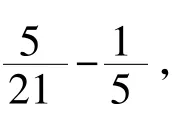
师：观察问题一、问题二的解决过程，你觉得异分母分数加、减法怎么计算？需要注意什么？

生1：我认为异分母分数加、减法先通分，再按照同分母分数加减法的计算法进行计算，所得的结果能约分的要约分，化成最简分数。

生2：我提醒大家：通分通常用分母的最小公倍数最为公分母，这样计算给我们带来方便，要不然给计算带来麻烦。

三、案例反思

“学校中学习的本质就是在教师的介入下，学生自立地、合作地进行活动。”基于这一点，我们的课堂应该呈现出一个师生对话、生生互动、组间交流的景象。在这样的课堂中，学生独特的思维得以展现，个性得以张扬，差异性教学得以体现。有个名人说过：“如果你有一种思想，我也有一种思想，而我们彼此交流这些思想，那么我们每个人获得了两种思想。”如此，课堂就因学生的差异而丰满，因学生的差异而充满智慧，因学生的差异而显得更加显得灵动。

（一）前置性学习是差异的源泉

本课例是苏教版《数学》五年级下册第八单元“分数加法和减法”的第一课时。这是异分母分数加减法，是在学习过同分母分数加减法，分数的基本性质，约分和通分的基础上进行教学的，显然学生有能力自悟。基于这样的想法，教师可设计上述“前置性学习问题”，让学生在课前先行充分的独立思考，培养孩子独立解决问题的能力，也为课堂上的充分交流、展示奠定基础。

如“问题一”安排的三个思考是：如何解决这个问题？还有其他的解决办法吗？比较这几种解法，你有什么想法？为什么会这样设计呢？由于学生智能有差异，已有的知识经验水平亦有较大的差异，他们必然会从不同的角度和层面去思考。正因有了这样的差异才会为课堂精彩的交流，思维的碰撞提供可能，也为个性化教育提供可能。

（二）充分的互动是展示差异的平台

之前的课堂教学片断所呈现出来的小组内的生生交流，让每个学生课前的独立思考有了一个阐述、厘清的机会，也让他们分享到了其他同学与自己不同的思考方式及过程，为进一步的交流和思考的深入做好了准备。组内的生生交流不仅仅是彼此思维的碰撞，更重要的是让每个学生都有展示自我的机会。而组际间的交流，则展现了准备充分的各种思考，在此基础上，认同、质疑、辩论才有了可能。学生在这样的交流中构建了自己的知识体系。

正是学生的充分展示，显得这种差异更加凸显，更加丰富，更加鲜活。课堂才显得更加有生命力，课堂才是真正意义上学生的舞台。因而，课堂上组织学生进行生生间、师生间、组际间的交流，使得呈现出的观点更贴近孩子的思维特点和方式，让每个孩子得以展示，得到关注和发展。

（三）智慧点拨是品味差异的良方

学生的交流很容易出现“萝卜烧萝卜”现象，很难使得知识的深度理解，这就需要教师通过合适的问题设计，在恰当之时，关键之处，把学生的思维引向深入即所谓的“智慧点拨”。例如问题一中，学生解决问题交流了三种方法，此时教师提出“虽然这三种方法解题的过程不同，但是有一个共同点是——”，教师的这一设问，把孩子的思维聚焦到问题的本质——异分母分数加减法为什么要先通分后才可以计算。问题二中，“你觉得异分母分数加减法怎么算？需要注意什么？”就这样简单的一问把学生的思维从具体引向抽象。

这样，将问题聚焦于学生理解知识的核心部位，帮助学生形成认识。这样的出手，既是课前的预设，更是课中的生成。依据学生的展示，不断调整提问的内容和方式，引导学生自主建构，不断提升解决问题的能力。

相信，我们善待学生的差异，课堂将会真正成为学生的课堂，课堂将会变得更加灵动！

张华伟）