数学教学中有效利用“错误”资源的策略

颜美芳

（台州市玉环县清港镇初级中学，浙江 台州 317000）

数学教学中有效利用“错误”资源的策略

颜美芳

（台州市玉环县清港镇初级中学，浙江 台州 317000）

学生在学习中出现的错误是一笔宝贵的教学资源，教师不但要宽容学生的错误，更要利用错误资源，因势利导，培养学生正确归因错误，进而提升学生的思维品质。

容错；辨错；用错；思错

正确有效地指出学生在学习过程中所出现的错误是初中数学教学的基本要求之一，教师要用资源的眼光看待学生的错误，让学生在纠错、改错中感悟道理，领悟方法，发展思维，实现创新，促进学生的全面发展。

一、容错——培养学生良好的思维品质

“学生的数学学习过程是一个自主构建，自己对数学知识的理解的过程”。在教学过程中，教师应启发诱导、点拨激疑，热情地邀请学生来回答问题，哪怕学生只是错误的一点想法和思路，都要引导学生积极整理思维过程，寻找错误原因。数学学习过程实际上是一个不断提出假设，修正假设，使学生对数学的认知水平不断复杂化，甚至趋于成熟的过程。

（一）漏解探因，培养发散性思维

许多学生在解题时往往满足于求出一解，导致不完整解题。引导学生探究分析出现漏解情况的原因，积累经验，强化数学分类的严密性，分类标准的科学化，促使学生的思维水平有层次、有步骤地向更优化的方向发展。

[案例1]为美化环境，在某小区内用30m2的草皮铺设一条长为10m的等腰三角形绿地，求这个等腰三角形绿地的另两边长。

引导学生思考时，不能忽视图形的位置或形状，应寻找出它们的内在联系，探索出一般规律，思维方式不能单一，对基本图形的基本性质和图形关系要熟练掌握，且能正确运用。因此，对于本题不仅要考虑到图形的基本性质还需考虑到图形的位置或形状。在这两个基本原则的基础上再制定分类标准时，可以先按图形的性质分成AB为底边与AB为腰两大类后再依据图形的位置关系即以高CD在△ABC的形内、形外两个角度再对前两类进行细化分类，当然亦可先考虑图形位置再考虑图形性质进行分类。

（二）排除思维定势，培养思维的严谨性

在刨根究底的纠错过程中，引导学生内化知识，自觉对自己的认知活动进行回味、思考、总结和调节，构建更清晰、稳定、条理化的知识结构。

[案例2]：学习了第三章第一节《直线与圆的位置关系》后，我发现作业本上的一个题目很多学生做错了。

题目：如图4，点A在⊙O上，sinB=1/2，能否判定直线AB和⊙O相切？请说明理由.显示题目后，仍然有极大多数学生喊出来相切.先让学生说一说相切的理由.生1：∵sinB=1/2，∴△OAB是直角三角形.即OA⊥AB，∴AB是⊙O的切线.

师：sinB=1/2，为什么△OAB是直角三角形呢？

生 2：∵sinB=1/2，

∴蚁B=30°.∵蚁B=30°，∴蚁O=60°.

∴蚁OAB=90°

师：蚁B=30°，为什么蚁O=60°呢？

生3：∵在直角三角形中，∴蚁B=30°，得出蚁O=60°

师：哪里说是直角三角形呢？

若说是直角三角形了，还需要∵蚁B=30°，蚁O=60°，∴蚁OAB=90°吗？

生4：这很简单.∵sinB=1/2，锐角三角函数值只能在直角三角形中求出来的.

∴是直角三角形.

师：对啊！锐角三角函数值只能在直角三角形中求出来的.

现在是已知蚁B的正弦值了.还用求吗？

生5：（看样子，这位学生急不可待想说）∵sinB=1/2，已知直角边等于斜边的一半了，怎么不会是直角三角形呢？

师：怎么了？

生6：还不知道是直角三角形又默认是直角三角形了.

师：对呀！那么sinB=1/2，只说明了什么呢？

生7：只说明了蚁B=30°.其他的角是多少度还不能说明.

“学生的数学学习是建立在经验基础上的一个主动建构的过程”。案例中，学生对锐角三角函数的概念还比较模糊，由于受先前经验的影响，想当然得出三角形是直角三角形。当学生出现错误时，教师给学生足够的时间和机会去发现、纠正错误，从而使学生的知识主动建构，形成正确的知识。学生的奇思妙想在教师的宽容、鼓励下，常可取得意想不到的效果，从而增强学习的积极性和自信心。

二、辨错——深化学生对知识本质的理解

在学习过程中，不同的学生具有不同的知识背景、不同的情感体验、不同的表达方式和参差不齐的思维水平，因此出错在所难免。教师不应将错误视之为洪水猛兽，唯恐避之不及，以一个“错”字堵住学生的嘴，再接二连三地提问，直至得出“正确答案”；或亲自“上阵”，把正确答案“双手奉上”。可以想到，不让学生经历实践、获得体验，企图直接拉住学生迈向“错”的脚步，结果就可能阻断他们迈向成功的道路。

[案例3]在探索分式方程“增根”产生的原因之后，笔者出示了一解方程的错解：x2=3x，等式两边同时除以x得x=3，对于这个结果学生惊奇了，他们发现这与他们用常规解法得出的解少了一个根——x=0，这极大地提高了学生的学习兴趣，并产生了认知冲突，从而给学生创造一个寻找“错误”的机会，学生很自觉地去寻找此解法的错误原因。不长时间就有学生站起来回答说：方程两边不能都除以x，因为只有x确保它不为0时才可以使用，而此题x=0恰好是这个方程的一个根，这就出现了“失根”的情况。笔者又适时出示了另一解方程的错解：x=6x,两边都除以x得：1=6，此题同样因为错误地运用了等式性质2，致使出现了荒唐的结果。这样的教学将课堂的主动权交给学生，让学生在辨错的过程中发现了知识的联系点，巩固了等式性质2的应用，相信学生在今后的学习中碰到应用等式性质2的时候会“小心行事”，避免重蹈覆辙。

“学生的错误都是有价值的”，教师不仅应该引导学生在回味疑惑、反思的境界中“去粗取精，去伪存真”，还要适当地设置一些有一定思维价值、能激发学生惊奇感的问题，让学生在辨析错误的同时激发学生学习探索的兴趣，并带着如何解决这些问题的强烈愿望去迁移知识、分析思考，从而加深对知识本质的理解。

三、用错——激发学生创新思维

英国心理学家贝恩布里奇说：“错误人皆有之，作为教师不利用是不可原谅的。”在数学教学中企图让学生完全避免错误是不可能的，也是没有必要的。而课堂上发生的错误并非是一文不值的，它往往反映了学生的思维能力，反映了学生的真实想法，这其中总会包含着合理的成分。教师应该善于巧用错误，善于发现错误背后隐藏的教育价值，引领学生从错中找出合理的一面，从错中找出与正确方法之间的联系，把“错误”资源巧妙地予以运用，不仅能让学生尽快走出误区，并能激发学生的创新思维。

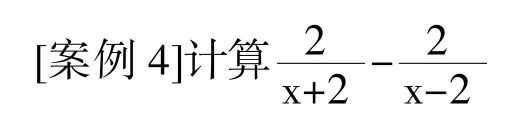
在一次初三数学复习课中发现很多学生做错了，下面是大多数学生错误的解法：

解：原式=2（x-2）-2（x+2）=2x-4-2x-4=-8

显然，解法错了，“张冠李戴”把方程变形搬到计算题上，把分式的化简当作分式方程，乘以（a+1）（a-1）进行去分母.于是教师来一个“顺水推舟，将错就错”，启发学生：刚才很多同学把分式的化简当作分式方程来解，虽然解法错了，但给我们一个启示，若能将该题去掉分母来解，其“解法”确实简洁明快，因此我们能否考虑利用方程来解它呢？于是一个新颖的解法就出来了.

案例中，教师没有让“错误”溜走，而是让学生的思维再现在大家面前，却发现这“错误”激活了学生，引发了学生创造性思维的不停涌现。

四、思错——培养学生自我评价能力

学生的错误不可能单独依靠正面的示范和反复的练习得以纠正，必须有一个“自我否定”的过程，而“自我否定”又以自我反思作前提。在实际教学中，教师应及时对学生在学习中出现的典型错误以及错误产生的原因，矫正的对策进行搜集、整理、记录。可以通过多种形式进行对比练习，让学生辨析提高。

笔者在教学实践中注重培养学生学会积累的习惯，其中一项重要的举措就是要求每位学生准备一本《错解解析本》。

具体操作如下：（1）保留错误：把错误题及原始的解题过程剪下来贴在“纠错本”本子里。（2）错误分析：让学生用自己的简短的语言描述错误的原因。（3）订正错误：要求学生用红笔把正确的解题过程订正在错解的下方，并在其四周圈上，起到醒目、告诫的作用。（4）解题心得：比如“本题采用数形结合的方法，快而正确”、“少图的几何题往往是多解题”、“一提二套三分四查,将因式分解进行到底”等。刚开始总是会忘记，感到厌烦，在经过督促检查、评比展览等措施后，大部分同学不仅能够做到自觉去摘录，而且还加了自己的特色，比如在笔记本的页眉、页脚加上一些名言警句，摘抄一些数学故事。

通过对错题进行纠错，使学生反思产生错误的原因，并且知道错误所在及改正的方法。这样可以进一步深化学生对所学的知识的理解、掌握及应用，实现从感性知识到理性知识的深化。

总之，学生不出错的教学，不是真正的教学，学生不出错的课堂不是好课堂。为此，教师在教学中要善于捕捉或创设数学活动的时机，为学生提供创造的机会。作为新世纪的新型教师，我们应该以学生的发展为本，不仅要用一颗“平等心”、“宽容心”去正确对待学生在学习中出现的错误，并且要巧妙、合理地处理好学生的“错误”这一教学资源，使学生在思维能力、情感态度与价值观等多方面得到进步与发展。

[1]薛法根.错误的价值[J].江苏教育，2007（2）.

[2]吴佳.浅谈初中数学教学中的“设陷”问题[J].中学数学教学参考（初中版），2007（11）.

[3]陈宇.失败也有营养[J].江苏教育，2008（3）.

[4]王飞君.突破题海战术 重视解题后的反思[J].中国数学教育（初中版），2007（4）.

张华伟）