一类期望值模型的SAA法收敛性分析及应用

胡伯霞，陈 源，李 龙

（衡阳师范学院 数学与计算科学系，湖南 衡阳 421002）

0 引 言

本文考虑如下随机规划问题：

这里X是一非空凸集，x是决策变量，ξ：Ω→Ξ⊂Rk是定义在概率空间（Ω，F，P）上的随机变量，E［·］是期望值算子，f：Rn×Rk→R，g：Rn×Rk→Rm是局部Lipschitz连续函数。

在许多情形下，对于给定的决策x，精确求解（1）中的期望值或不可能或代价太高，为了克服这一困难，我们可以考虑运用众所周知的采样平均近似SAA法来求解［1－3］。Wang和Ahmed［4］考虑了一类随机规划模型：

Xu和Zhang［5］考虑了一类随机规划模型：

Liu和Xu［6］还考虑了一类具有随机二阶占优约束的随机规划问题：

受上述方法的启发，本文研究（1）的数值求解方法。设通过计算模拟或从历史数据已获得ξ的采样ξ1，ξ2，…，ξN，考虑（1）的如下采样平均近似问题：

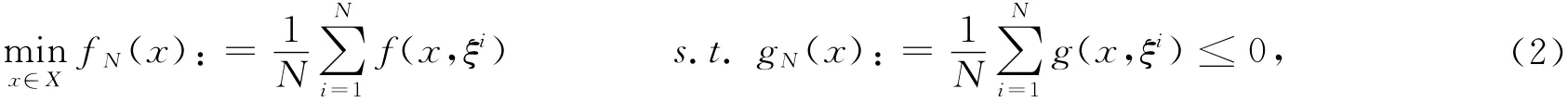
称（2）为SAA问题，而称（1）为原问题。SAA问题的主要优点是无需计算期望值。

1 精确罚方法

假设已获得（2）的一个最优解，记为xN，我们需要分析随着样本规模N的增大，xN的收敛性。显然直接从（2）分析将会非常复杂，因为（2）的约束个数也会随着N的增大而增大，为了避免这一问题，我们把（1）和（2）运用精确罚技术将问题归结为在约束确定的情况下，分析目标函数的逼近性质上来。记

对应于原问题（1）的精确罚规划为：

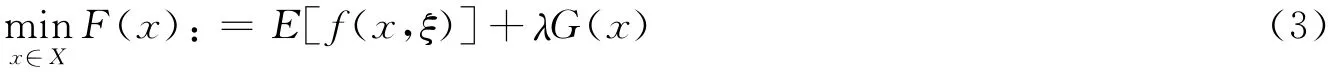
其中λ是罚参数。在适当的假设下（1）与（3）的最优解等价。

假设1.f（x，ξ）和g（x，ξ）关于x是局部Lipschitz连续，且它们的模由一可测正函数κ（ξ）界定。

类似于文献［5］的证明，我们有下面的最优解等价性定理：

定理1.假设原问题（1）满足Slater条件且X是紧集，若假设1成立，则存在一个正数，使得对任意λ＞，（1）与（3）的最优解集相同。

对应于SAA问题（2）的精确罚规划为：

其中λN是罚参数。

对于（2）与（4）的最优解有如下等价性定理：

定理2.若定理1的假设成立，那么存在正数N＊和λ＊使得对任意N＞N＊和λN＞λ＊，（2）与（4）的最优解集w.p.1一致。

2 收敛性结果

本小节主要研究FN（x）→F（x）的一致指数收敛性，同时这也得出了xN→x＊∈X＊，N→∞，而X＊为原问题（1）或SAA问题（3）的最优解集。另外从计算方面来讲，也需要在给定误差界d（xN，X＊）的情况下估计采样样本数N。在采样为独立同分布（iid）或非独立同分布（non－iid）的情况下，应用大偏差理论（LD）分析统计量的指数收敛性，请参看文献［2］［3］［7］。这里假设采样为广义采样。

定义下面两个矩量母函数：

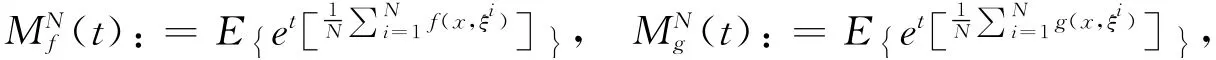
引理1【逐点指数收敛】若假设2成立，则对任意x∈X和小正数ε＞0，只要N充分大则有

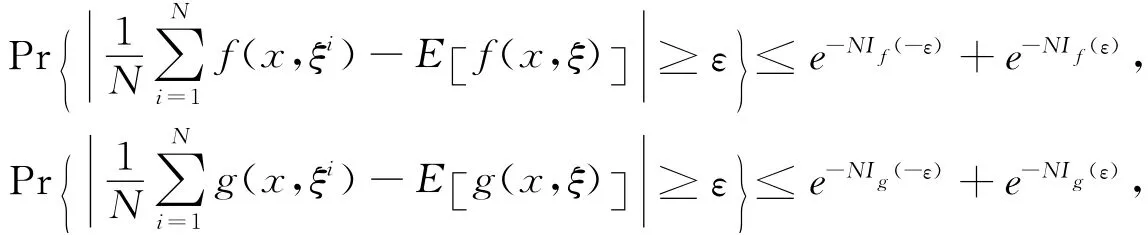
在上述假设和引理下，有下面的一致指数收敛性定理。

定理3.若假设1，2，3成立，且λN→λ＊，N→∞。则∀ε＞0，存在与N无关的正常数c（ε）和β（ε），使得

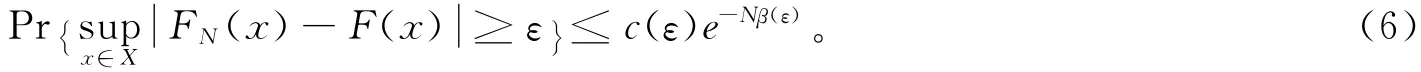
证明：首先有：

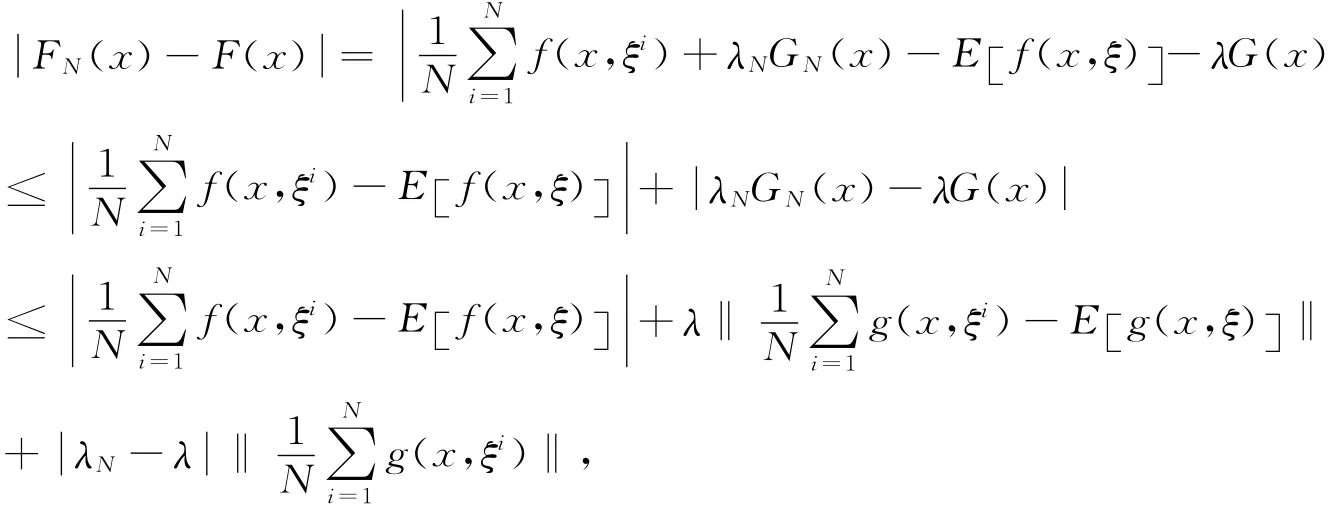
接下来，估计

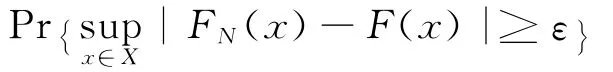
由文献［8］，存在cl（ε），βl（ε），l＝1，2，3，使得

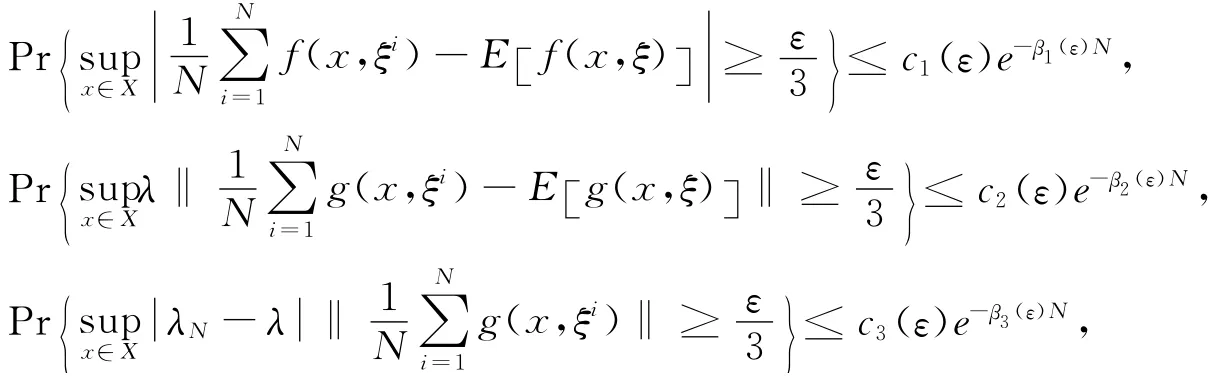
联合上面五式，有

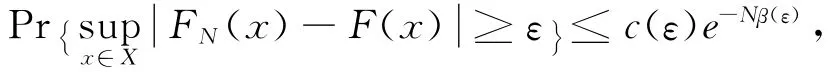
其中c（ε）＝c1（ε）＋c2（ε）＋c3（ε），β（ε）＝min｛β1（ε），β2（ε），β3（ε）｝。得证。

引理2 考虑一般优化问题

这里p：RN→R，X⊂RN，和一个扰动规划问题

根据上述引理仿文献［5］的证明可得如下收敛性结果。

定理4.假设如定理3.若x｛N｝是SAA问题的最优解序列，而X＊是原问题的最优解集，则对任意ε＞0，存在正常数c（ε）和β（ε），使得

3 数值实验

例 考虑如下期望值优化问题：

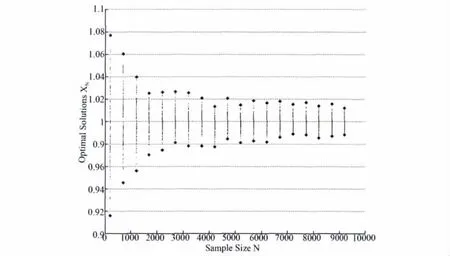
图1 SAA问题的收敛性（σ＝0.5）

［1］S M ROBINSON.Analysis of sample－path optimization［J］.Math.Oper.Res.，1996，21：513－528.

［2］A DEMBO，O ZEITOUNI.Large Deviations Techniques and Applications［M］.New York：Springer－Verlag，1998.

［3］A SHAPIRO.Monte Carlo sampling methods，in：A.Rusczynski and A.Shapiro（editors），Stochastic Programming［M］.Handbooks in OR ＆MS，Amsterdam：North－Holland Publishing Company，2003.

［4］W WANG，S AHMED.Sample average approximation of expected value constrained stochastic programs［J］.Oper.Res.Letters，2008，36：515－519.

［5］H XU，D ZHANG.Monte Carlo Methods for Mean－Risk Optimization and Portfolio Selection［EB／OL］.［2010－6－3］.Comput.Manag.Sci.，http：／／www.2010，DOI 10.1007／s10287－010－0123－6.

［6］Y LIU，H XU.Stability and Sensitivity Analysis of Stochastic Programs with Second Order Dominance Constraints［EB／OL］.［2010－6－17］.http：／／eprints.soton.ac.uk／182199／1／Liu－Xu－17－June－2010.pdf

［7］A SHAPIRO and H XU.Stochastic mathematical programs with equilibrium constraints，modeling and sample average approximation［J］.Optimization，2008，57：395－418.

［8］H XU.Uniform exponential convergence of sample average random functions under general sampling with applications in stochastic programming［J］.J.Math.Anal.Appl.，2010，368：692－710