非线性数据拟合对重叠峰信号的分离
袁红志,游开明,谭延亮
(衡阳师范学院,湖南 衡阳 421008)
0 引 言
在化学领域,重叠的色谱峰,重叠的伏安峰和重叠的光谱信号等是比较常见的。由于重叠现象的存在,需要对信号进一步的分离得到各子峰的参数才能对其定性和定量分析。分离重叠峰信号有两个步骤:(1)重叠峰的分辨。目的在于提高重叠峰中子峰的分辨率或将不明确的峰位置分辨清楚。主要有导数分峰法[1]、Fourier去卷积法[2]、微分消卷积法[3]和小波分析及其改进法[4]等。这些方法能提高峰群中的各子峰的分辨能力,但不能彻底形成分峰,也不能得到各子峰的参数[5];(2)重叠峰信号的分解。目的是获取重叠峰中各子峰的信息,即将提高分辨力后的峰信号进一步分解成独立的子峰。一般采用高斯峰、洛仑兹峰或这两种峰以不同的比例组合作为模型来拟合需要分解的重叠峰信号,得到各子峰的形状、位置和面积等信息,通常称作曲线拟合法[6]。本研究利用最小二乘法[7]对重叠峰信号的数据进行非线性数据拟合得到各子峰的函数表达式,将传统的峰分辨和峰分解两个步骤合二为一,简化了重叠峰信号分析过程。
1 理论分析
高斯峰信号的函数表达式为:

洛仑兹峰信号的函数表达式为:

由式(1)、(2)可知,在已知各子峰类型的条件下,只要在重叠峰中得到各子峰A、u、σ这三个参数,就可以得到高斯峰或洛仑兹峰信号的全部信息。相邻独立峰的重叠程度分离度用下式表达[8]:
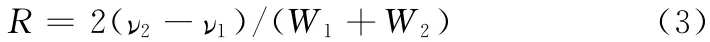
式中,ν1和ν2分别表示相邻重叠峰的峰位置,W1和W2表示独立峰的半峰宽。R表示分离度,其值越大,两个独立峰的分离度越大,重叠程度越小;反之,其值越小,分离度越小,重叠程度越大。
峰高一半处的峰宽度,称为半峰宽。高斯峰信号的半峰宽由式(1)可知:
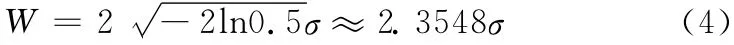
洛仑兹峰信号的半峰宽由式(2)可知:

高斯峰与高斯峰的分离度为:
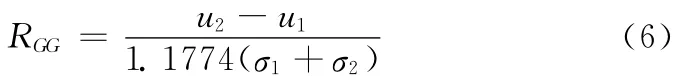
高斯峰与洛仑兹峰的分离度为:

实际采样得到的重叠峰信号都有测量误差,表现为噪音信号,测量值围绕理论值上下波动。最小二乘法是数据处理和误差估计中常用的数学方法,可以依据对某事件的大量观测而获得“最佳”结果或“最可能”表现形式,因此可以利用其来分离重叠峰,得到各子峰的函数表达式。

重叠峰信号可以表述为如下形式:在等精度测量时,采样步长为h,可以定义优值函数:

f(nh)表示不同采样点重叠峰的实际测量值,当A1,u1,σ1,A2,u2,σ2取最佳值时,优值函数X12(A1,u1,σ1,A2,u2,σ2)取极小值,有:
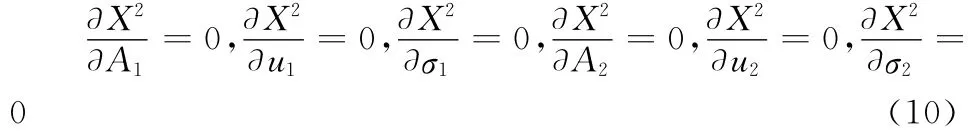
利用式(10)非线性拟合可以得到的A1,u1,σ1,A2,u2,σ2值,即各子峰的函数表达式。非线性拟合计算量大,数值计算存在全局最优和局部最优的问题,初值选择的不当,可能导致计算结果误差更大,当前搜索算法中较快的是Levenberg-Marquardt方法。
2 重叠峰信号分离仿真研究
模拟的含噪音重迭峰信号由下式产生:

噪音信号仿文献[1]表示为:
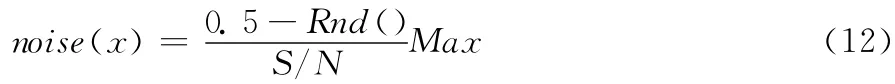
Rnd()函数返回一个小于1但大于或等于0的随机数值。Max表示重叠峰信号强度的最大值,S/N表示信噪比,令其为20。
对于重叠峰,子峰的分离度越小,分离越困难。下面对分离度分别为0.75,1的仿真重叠峰进行分离。采样点为200,步长为0.05。
A 高斯-高斯峰重叠信号的分离:
令A1=20,u1=4,σ1=0.8,A2=10,σ2=0.8,u2由分离度确定。根据式(6)得到分离度分别为0.75,1时,u2分别为5.413,5.884;Max取值分别为22.55,20.68。
分离度0.75时高斯-高斯峰重叠信号如图1所示,可以发现该信号左、右边的上升、下降速率不同,用单高斯函数非线性拟合后更加明显。用单高斯函数非线性拟合后的优值函数取值为:119.606。用双高斯峰非线性拟合的结果如图2所示,其优值函数取值为:21.862。观察图1、图2可知,用双高斯函数非线性拟合结果较佳,优值函数取值也证明了该信号是重叠的信号,不是单高斯峰。对分离度分别为0.75,1的高斯-高斯峰重叠信号分离结果见表1。

表1 非线性拟合结果及相对误差(%)
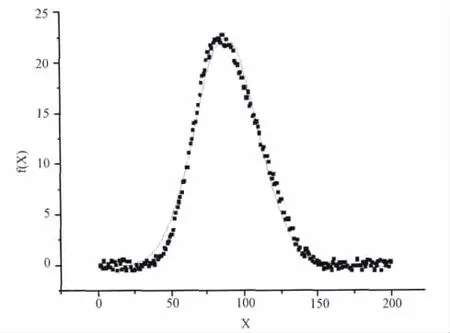
图1 分离度为0.75时高斯-高斯峰重叠信号及用单高斯函数非线性拟合结果
B 高斯峰与洛仑兹峰重叠信号的分离
令A1=20,u1=4,σ1=0.8,A2=10,σ2=1,u2由分离度确定。根据式(7)得到分离度分别为0.75,1时,u2分别为5.456,5.942。Max取值分别为23.37,22.14。
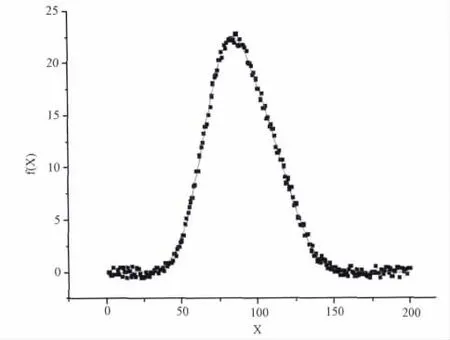
图2 分离度为0.75时高斯-高斯峰重叠信号及用双高斯函数非线性拟合结果
分离度0.75时高斯-洛仑兹峰重叠信号如图3所示,可以发现该信号左、右边的上升、下降速率不同,用单高斯函数非线性拟合后更加明显。用单高斯函数非线性拟合后的优值函数取值为:210.348。用高斯-洛仑兹峰非线性拟合的结果如图4所示,其优值函数取值为:22.488。观察图3、图4可知,用高斯-洛伦兹函数非线性拟合结果较佳,优值函数取值也证明了该信号是高斯-洛伦兹峰重叠信号,不是单高斯峰。对分离度分别为0.75,1的高斯-洛伦兹峰重叠信号分离结果见表1。
从表1可以看出分离度大于0.75的高斯-高斯峰、高斯-洛仑兹峰重叠信号都可以有效的分离出子峰,得到的子峰参数误差较小。

3 结 论
利用非线性数据拟合含噪音的重叠峰数据,得到各子峰的参数。通过仿真分析发现该方法对分离度仅为0.75的重叠峰的分离也有很好的效果。在分离度相同时,对高斯-洛仑兹峰重叠信号分离的相对误差小于对高斯-高斯峰重叠信号的分离;得到的各子峰参数相对误差随分离度的提高而减小。该方法可用于实际的含噪音重迭峰信号进行处理。
[1]卢小泉,刘宏德,张敏,等.分数导数结合傅里叶最小二乘拟合处理含噪音的重迭信号[J].分析化学,2003,33(2):143-147.
[2]Sten O E.The Fourier transform of voltammnetric peak and its use in resolution enhancement.[J].Electroanal Chem,1990,296:371-394.
[3]方建兴,吴茂成,王定兴.微分消卷积法提高重叠谱图的分 辨 率[J].光 谱 学 与 光 谱 分 析,1998,18(6):666-668.
[4]王瑛,莫金垣,陈晓燕.二阶样条小波卷积法分辨重叠化学信号[J].中国科学B辑:化学,2003,33(04):296-305.
[5]李一波,黄小原.基于RBFNN和GA的重叠峰分辨技术[J].应用科学学报,2002,20(1):99-103.
[6]Huang W,Henderson T L E,Bond A M,et al.Curve fitting to resolve overlapping voltammetric peaks:model and examples[J].Analytica Chimica Acta,1995,304(1):1-15.
[7]向前,林春生,程锦房.噪声背景下的盲源分离算法[J].数据采集与处理,2006,21(1):42-45.
[8]陈晓燕,莫金垣,邹小勇,等.基于分形理论分辨重叠峰的 新 算 法[J].高 等 学 校 化 学 学 报,2004,25(7):1221-1225.

