高阶离散Green函数的一个逐点估计
魏继东
(衡阳师范学院 数学与计算科学系,湖南 衡阳 421008)
0 引 言
离散Green函数在研究有限元最大模估计中起着非常重要的作用。文[1]给出了一阶离散Green函数定义并得出了相关性质,文[2]给出了离散Green函数的一个逐点估计。文[3]给出了高阶离散Green函数定义及性质,本文在[2]及[3]的基础上获得了高阶离散Green函数的一个逐点估计。
1 高阶离散Green函数定义及记号
考虑椭圆问题:

其变分形式为:
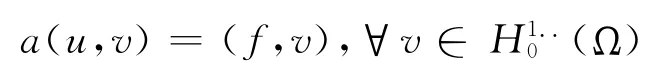
设Sh是有限元空间,引进高阶导数∂izG*z及其Galerkin逼近∂izGhz(i≥2)(参[3]),满足:

设B是半径为r的球,Bd是半径为r+d的同心球,熟知若u在Bd内调和,uh∈Sh则有:
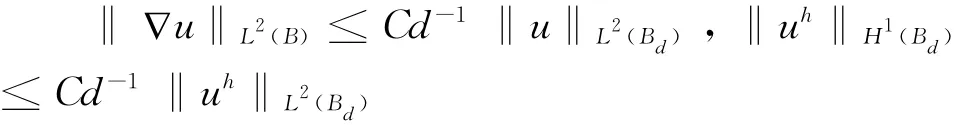
由文[2]有如下命题
命题1.若uh∈Sh,Bd⊂D⊂Ω满足a(u,v)=0,则:
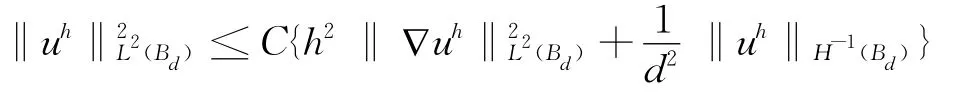
命题2.在命题1的假设下有:
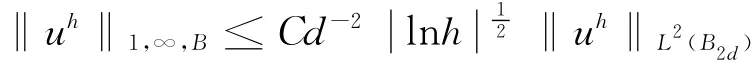
2 两个引理
引理1.设g=∂izGz,gh=∂izGhz,则对任意s≤k-1,有:
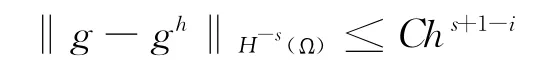
证明:先设g=∂izG*z,注意到
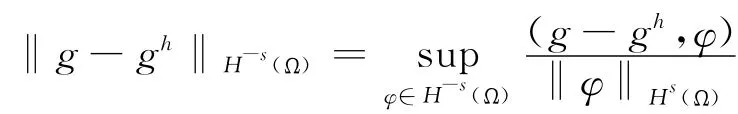

由文[3]性质1及插值估计有

再利用文[4]极限过度方法将g=∂izG*z换成g=∂izGhz结论依然成立。
引理2.设g=∂izGzgh=∂izGhz,存在常数C使得当k≥2时有
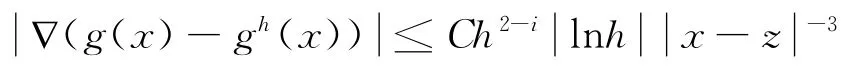
证明:设x为B的中心,,ω为B上的切断函数,令u1=ωg(x),uh1为u1的Galerkin逼近,uh2=gh(x)-uh1,则
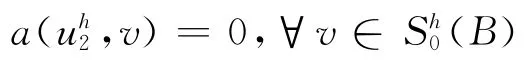
并且


为估计I2,将B做一点小修改使ω在B内有支集,设,则由命题1,命题2有:
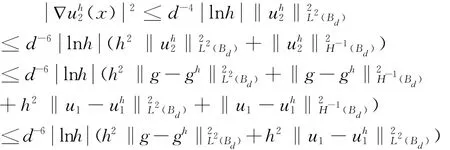
由文[3]性质2有:

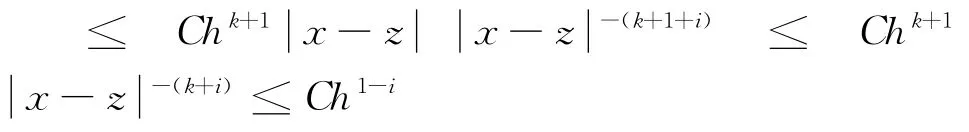
结合上面各式即得证引理,
3 主要定理
定理1.若存在常数C0使得,则有:
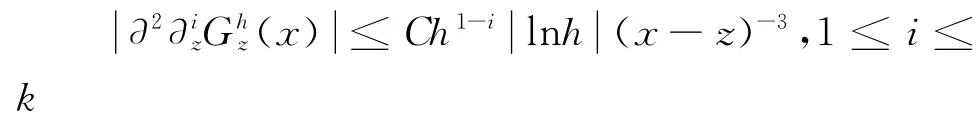
证明:设x∈e,z∉e,记d0=dist(z,e),则d0≥,应用逆不等式及引理2有

证毕。
[1]朱起定,林群.有限元超收敛理论[M].长沙:湖南科技出版社,1989.
[2]Lin,Q.,Zhou J.M.Superconvergence in high-order Galerkin finite element methods[J].Compute Methods in Applied Mechanics and Engineering,2007,196:3779-3784.
[3]魏继东,朱起定.离散Green函数估计的若干推广[J].邵阳学院学报:自然科学版,2008,5(2):13-14.
[4]谢锐锋.凹角域上的Green函数逼近的逐点估计和有限元外推[J].计算数学,1988(3):232-241.

