高斯波束传播特性研究

常 伟，张登玉，张宗兵，魏增飞

（1.西安电子科技大学 理学院，陕西 西安 710071；2.衡阳师范学院 物理与电子信息科学系，湖南 衡阳 421002）

0 引 言

随着激光的出现和光电子技术的发展，对高斯波束研究开始为人们所重视。Kogelnik［1－2］在傍轴近似的条件下，研究了高斯波束场的分布特性。对于高度平行的激光束，傍轴近似理论成功地解释了实验数据。然而，半导体激光器及大数值孔径光学透镜的广泛应用，标志着光源尺寸不断接近波长数量级甚至更小，波束发散角增大，傍轴近似条件不再满足。目前对于大角度波束的研究主要有三种方法，第一种是M.Lax提出的“微扰法”［3］，即将波束场量用无量纲的幂级数展开。Davis在M.Lax基础上给出场强的一级修正解［4］。第二种角谱法［5－7］则将高斯波束用平面波展开，根据边界条件确定角谱。第三种是曾小东［8］使用格林函数基于惠更斯原理直接求解波动方程得到了远轴高斯波束场表达式。

1 高斯波束及其性质

电磁场的任意直角分量u（x，y，z）都满足Helmholtz方程

波束场强在横截面上的分布由具体的激发条件确定［9］，考虑一种最简单的高斯分布，分布函数为e－（x2＋y2）／w2，波束的宽度w＝w（z），故u可以写成

其中eikz表示沿z方向的传播因子，不同于广延于全空间中的平面波所具有的确定波矢，波束只能有大致的传播方向。e－f（z）（x2＋y2）为限制波束宽度因子，g（z）表示波的振幅。

将g（z）和f（z）代入（2.2）式可以得到高斯波速场强函数［9］

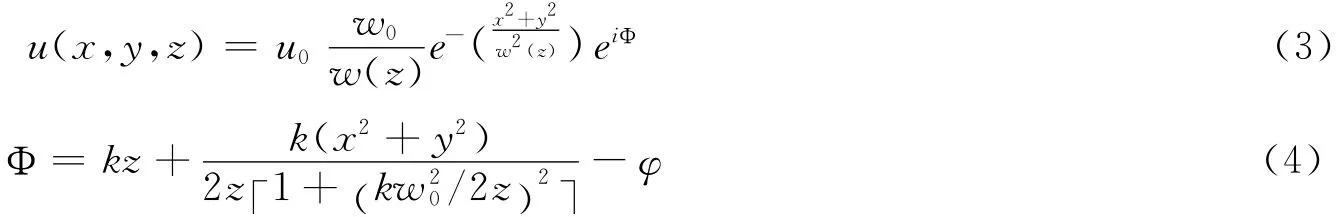
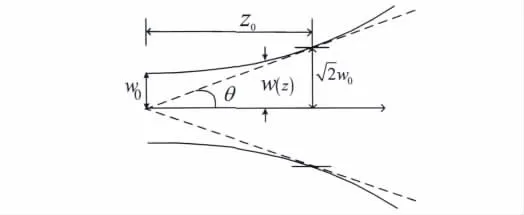
图1 高斯波束过轴线剖面

2 高斯波束场描述

2.1 傍轴近似理论

均匀各向同性无源介质中沿z轴方向传播的波束电场可以写成［10］

将Laplace算子分解成横向和纵向两部分［11］

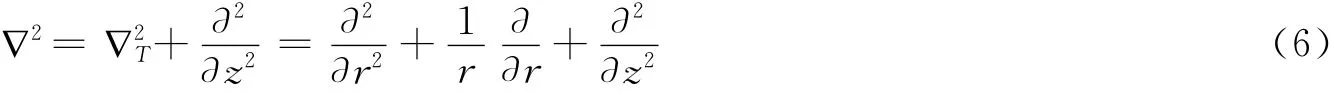
该方程解的最低阶模即为高斯波束，具有形式［12］

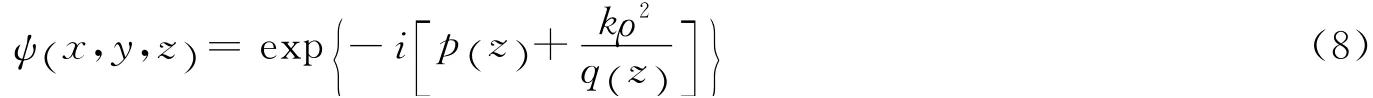
将（8）式代入（5）式，得到傍轴近似条件下的高斯波束解

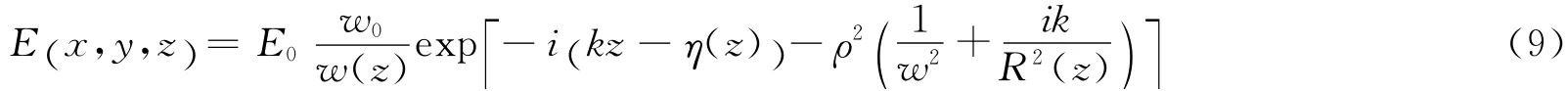
其中w（z）＝w0表示波束的尺寸，R（z）＝z（1＋z20／z2）表示波 前曲率半 径，η（z）＝tan－1（z／z0），z0＝nπw20／λ。为描述波束的发散特性，将波束的发散角定义为

其中n为介质折射率。对于平行度极好的激光束，傍轴近似理论与实验数据已经能高度吻合。

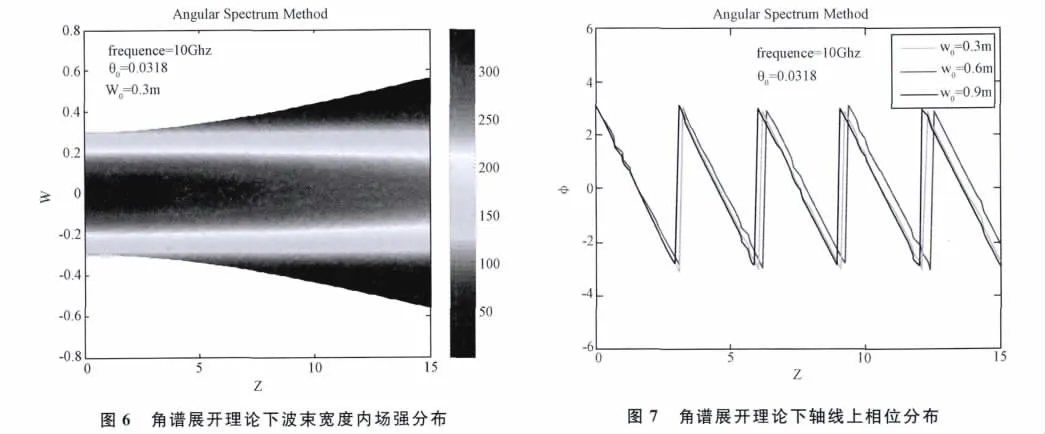
从高斯波束场强分布图可以看到场强集中在轴线附近，往两侧迅速衰减，当束腰半径变大时其相位沿z轴有向前移动的趋势。

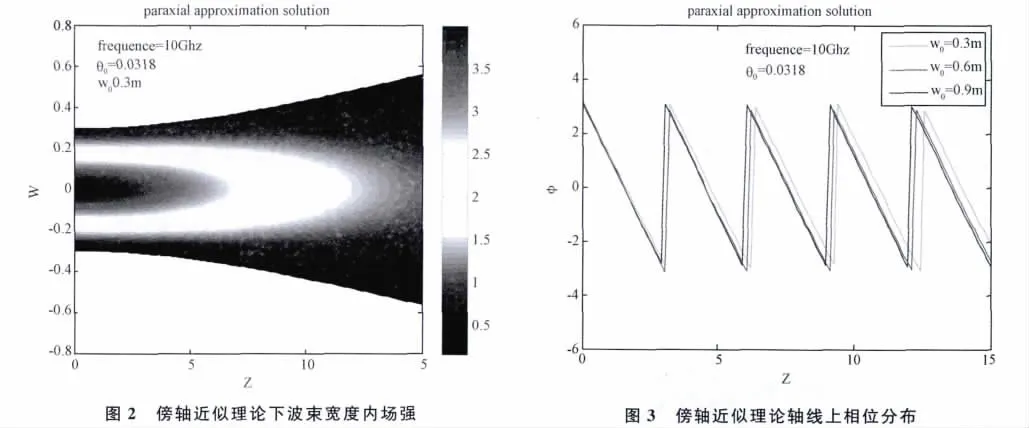
2.2 微扰法

傍轴近似理论在实验上获得了巨大的成功，却因为其只考虑场沿横向极化，忽略了纵向分量，以至于傍轴解与Maxwell方程不能自洽［3－4］。为此，Lax提出将波束场分解成横向和纵向两个分量，求解严格的Maxwell方程，并将场量用束腰尺寸与发散长度之比s＝w0／l＝1／kw0的幂级数展开，建立对傍轴各级修正的微分递推关系。Davis在此基础上给出了傍轴解得一阶修正表达式。

假设

在Lorentz规范下的满足Helmholtz方程

将（11）式代入（13）式得到

将（12）式代入（14）式得到

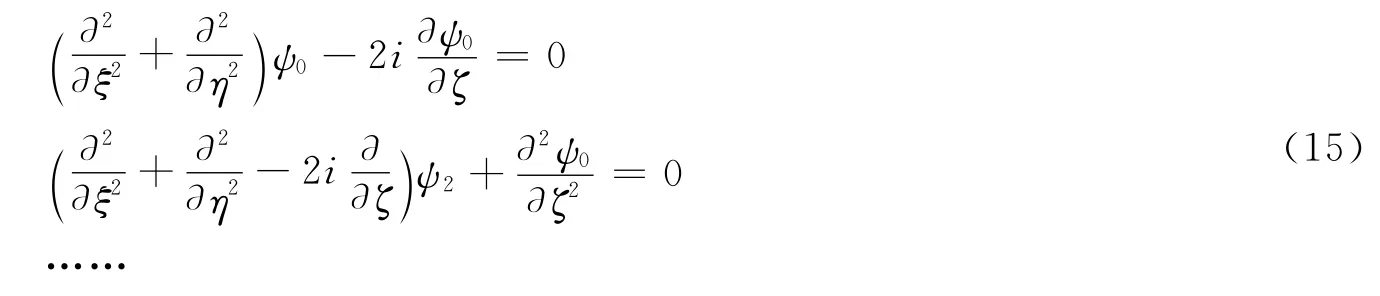
其中s＝w0／l＝1／kw0，ξ＝x／w0，η＝x／w0，ζ＝z／l，l＝kw20为共焦参数，当z＝l时，R取得最小值。求解（15）式得到

其中Q0＝1／（i＋2ζ），ρ2＝（ξ2＋η2）。根据电磁场与矢势的关系

得到修正后的波束电场

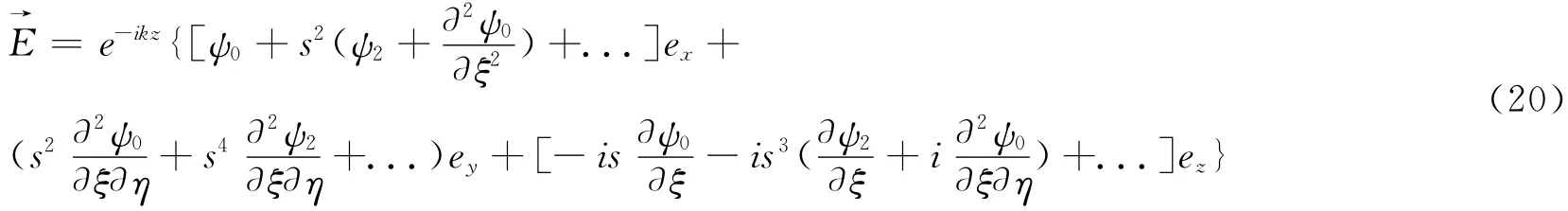
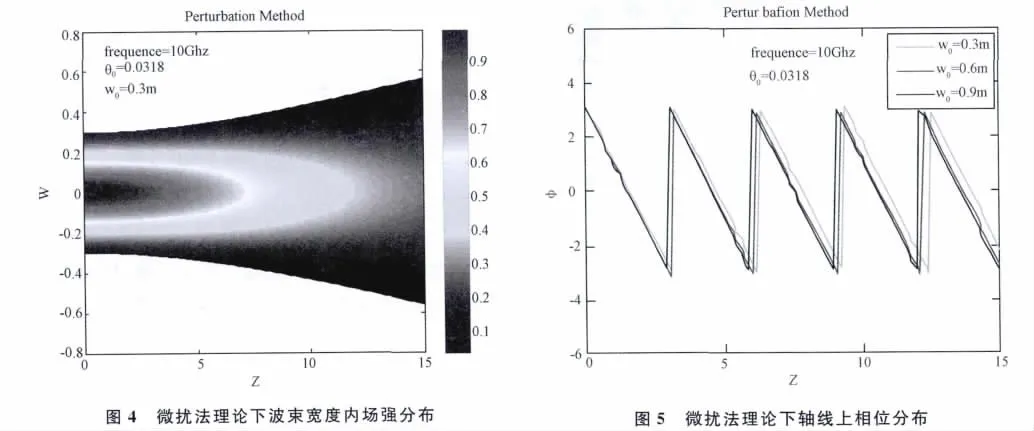
2.3 角谱展开法

当波长达到束腰半径数量级或者更小时，傍轴近似条件不再成立，而微扰法得到的电场表达式将非常繁琐。基于本征函数的角谱展开是Helmholtz方程在边界条件下的严格解，不受傍轴近似条件限制，能够用来研究傍轴区外场特性，而且场的角谱展开具有明显的物理意义，即空间波束可以看做是沿各个方向具有不同振幅的平面波的叠加［13］，这对研究波束与介质体的相互作用是很方便的。

设电场振幅在束腰平面内具有高斯型函数分布

在平面坐标系内，将电场用平面波谱展开，各分量的具体形式为［6］

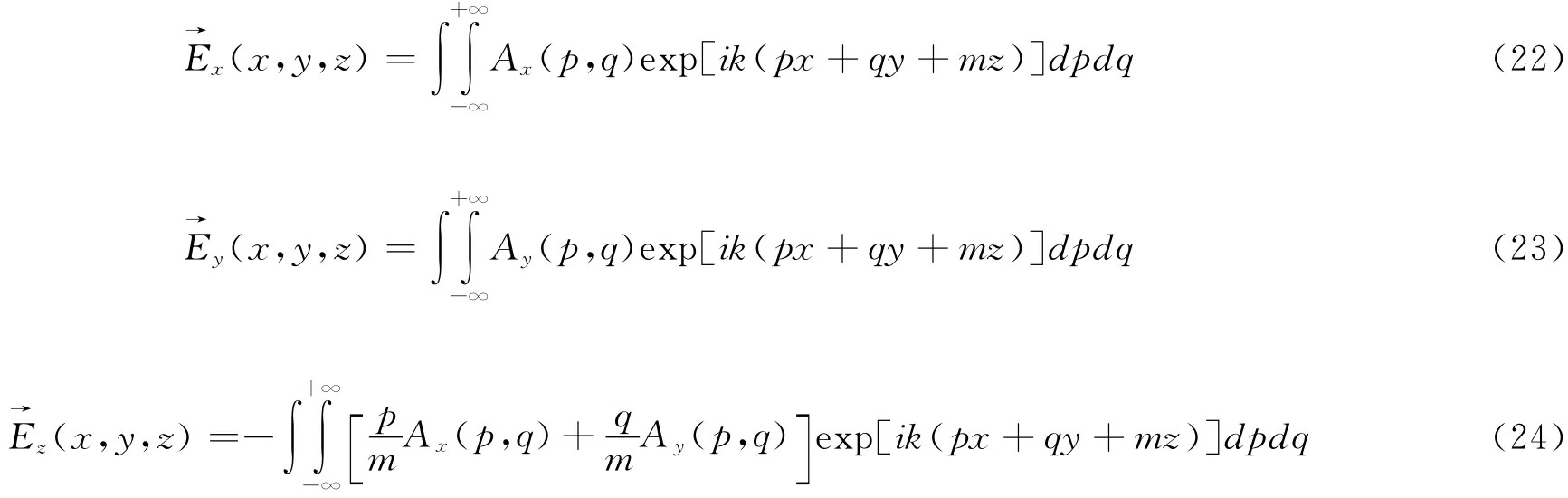
其中

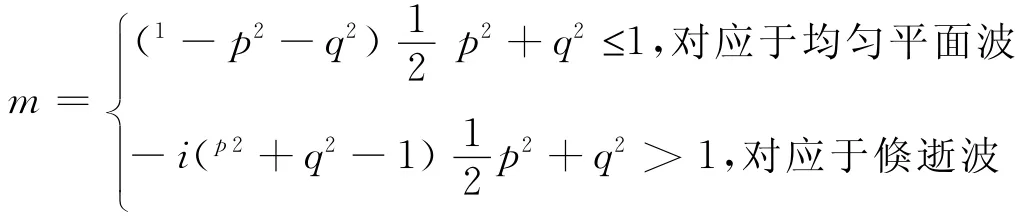
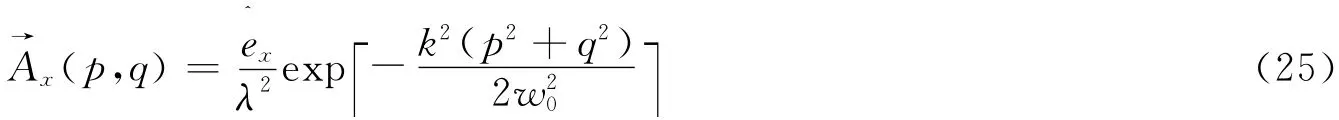
将（25）式再代入到（22）式，可以得到

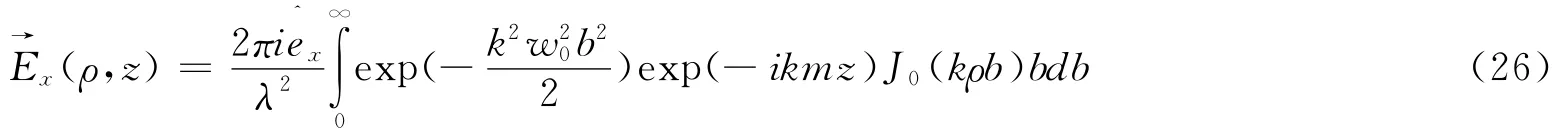
其中

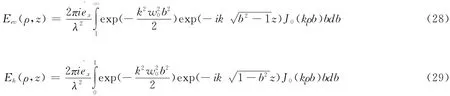
在远场时，倏逝波的贡献可以忽略，角谱展开法的远场解为

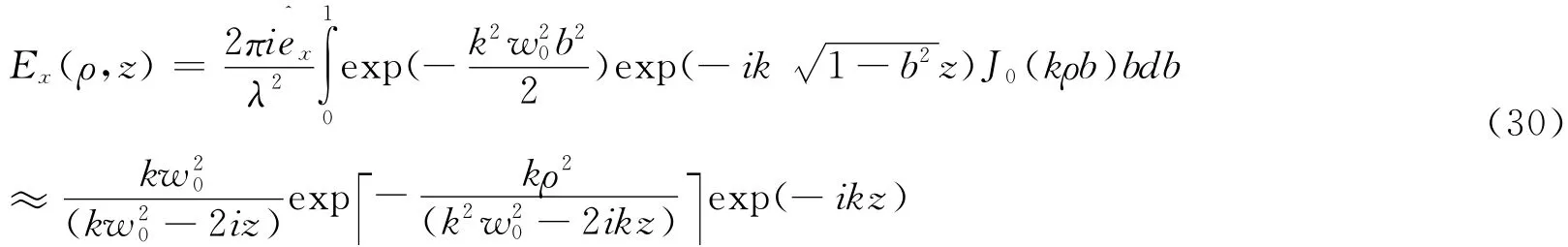
3 结 论

本文介绍高斯波束的基本理论，指出高斯波束与平面波的区别，平面波广延于全空间并具有确定的波矢，而波束只有大致的传播方向和一定的波束宽度，在波束腰部处其波阵面为平面，远离轴心处则为以腰部中点为球心的球面。分析比较了描述高斯波束的三种主要方法并基于角谱展开法推导波束场分量表达式，模拟了波束宽度内场强及其相位分布。研究发现，高斯波束场能量主要分布在轴线附近，远离轴线时呈指数衰减。对于近轴解，这三种方法都可以退化到同一形式，对于远轴解角谱展开法有着更明确的物理意义、更高的精度和更广的适用范围。

［1］Kogelink H，Li T.Laser beam and resonators［J］.Proc.IEEE，1966，54：1312－1329.

［2］Kogelink H.On the propagation of Gaussian beams of light through lenslike media including these with a loss and gain variation［J］.Appl.Opt.，1965，4c123：1562－1569.

［3］Lax M.From maxwell to paraxial wave optics［J］.Phys.Rev.A，1975，11c47：1365－1370.

［4］Dawis L.W.Theory of electromagnetic beams［J］.Phys.Rev.A，1979，19（3）：1177－1179.

［5］Simon R，Sudarshan E.C.G，Mukunda N.Cross polarization in laser beams.Appl［J］.Opt.，1987，26（9）：1589－1593.

［6］W.H.Carter.Electromagnetic field of a Gaussian beam with an Elliptical cross section［J］.J.Opt.Soc.Am，1972，62（10）：1195－1201.

［7］Doicu，T.Wriedt.Plane wave spectrum of electromagnetic beams［J］.Optics Comm.，1997，136：114－124.

［8］曾小东，梁昌洪，安毓英.远轴高斯波［J］.物理学报，1997，46（10）：1932－1937.

［9］郭硕鸿，黄逎本，李志兵.电动力学［M］.3版，北京：高等教育出版社，2008.

［10］张登玉，赵晗，高峰.左手介质中电磁波的传播速度［J］.大学物理，2006，25（12）：14－17.

［11］薛谦忠.粗糙面波束散射及其应用［D］.西安：西安电子科技大学，2000.

［12］张克潜，李德杰.微波与光电子学中的电磁理论［M］.2版，北京：电子工业出版社，2001.

［13］陈辉.粗糙物体高斯波束散射及在激光一维距离成像中的应用［D］.西安：西安电子科技大学，2004.