关于Halley法Julia集的对称性

刘 刚，陈少林，李浏兰

（衡阳师范学院 数学与计算科学系，湖南 衡阳 421002）

0 引言及主要结果

给定多项式f（z），则如下定义的公式

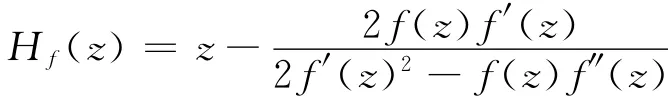
称为关于多项式f的Halley法。该法是一种重要的迭代找根算法，其被关注的程度仅次牛顿法。计算数学工作者对该法进行了大量的研究并取得非常丰富的成果，而从复动力系统的角度进行的研究以及取得的成果相对较少。K.Kneis［1］研究了Hf不动点的性质并给出了一些特殊多项式的Halley法的Julia集的分形图集。文献［2］对Hf的Julia集的拓扑结构进行了研究。

Julia集是复动力系统的基本研究对象，我们关心Julia集的拓扑，分形，几何等性质，鉴于多项式在迭代找根算法下一般都为有理函数，本文只在有理函数范围内进行研究。有理函数Julia集的对称性所研究的是有理函数的Julia集的自相似性，涉及的是Julia集的几何性质。A.F.Beardon［3］研究了临界有限的有理函数的Julia集的对称性。随后G.Levin［4］研究了临界有限的有理函数的Julia集的对称性。D.Boyd［5］分析了有理函数的Julia集具有平移不变性的情形。文献［6］对三类迭代找根算法Julia集对称性进行了研究。

给定有理函数R（z），则R的Julia集的对称群∑（R）为保持J（R）不变的共形欧氏变换σ构成的群，即∑（R）＝｛σ：σ（z）＝e2πθiz＋b（θ∈［0，1］）且σ（J（R））＝J（R）｝。给定非线性多项式f（z）＝anzn＋an－1zn－1＋…＋a1z＋a0（an≠0），我们称为f（z）的形心。如果an＝1且an－1＝0，则这样的多项式称为标准多项式。若f（z）为非标准的多项式，令，则T◦f◦T－1为标准多项式。结合关于多项式的Halley法的动力学性质和关于有理函数Julia集对称群的知识，我们获得了如下结果：

定理1 设f（z）为度大于1的标准多项式，则∑（f）⊂∑（Hf）。

定理2 设f（z）为度大于1的多项式，则平移变换σ＝z＋1∈∑（Hf）当且仅当J（Hf）为一水平直线。

定理3 设f（z）为度大于1的多项式，则J（Hf）为一条直线当且仅当f（z）＝c（z＝－z1）n（z－z2）n（c∈ℂ＼｛0｝，z1≠z2）。此时J（Hf）为连接z1与z2线段垂直平分线。

推论1 设f（z）为度大于1的多项式，则σ＝z＋1∈∑（Hf）当且仅当f（z）＝c（z－z1）n（z－z2）n（c∈ℂ＼｛0｝，z1≠z2，Re（z1）＝Re（z2））。

1 相关定义及引理

设R为复球面ℂ－上的有理函数，，其中P和Q为互素的多项式，degR＝max（degP，degQ）称为R的度。记Rn为R的第n次迭代。若存在m，k＞0使得Rk（Rm（z0））＝Rm（z0），则称z0为R的预周期点。特别地，当m＝0时，z0称为周期点，相应地最小的的k称为周期点z0的周期。若｜（Rk）′（z0）｜＜1，｜（Rk）′（z0）｜＝1或者｜（Rk）′（z0）｜＞1，则z0称为（超）吸性，中性或者斥性周期点。R的Julia集J（R）是定义为其斥性周期点的闭包。J（R）补集，即ℂ－＼J（R），称为R的Fatou集F（R）。J（R）是完全不变的，即R（J（R））＝J（R）＝R－1（J（R）。另外，J（R）没有完全不变的真闭子集。关于有理函数动力系统更多的定义和结果参见文献［7，8］。

为证明文中结果，我们还需以下引理。

引理1［3］设f（z）为度大于1的多项式，则对称群∑（f）是由以f（z）的形心为中心的旋转变换构成的。如果f（z）是标准的，而且∑（f）是有限的，则∑（f）的阶为使得f（z）可表示成f（z）＝zrQ（zm）的最大整数m，其中Q（z）为一多项式。如果对称群∑（f）是无限的，那么J（f）是一个圆周，并且f（z）共轭于zn，其中n＝deg（f）。

引理2［5］设R（z）为度大于1的有理函数，且J（R）＋1＝J（R）。如果无穷远点∞是预周期的，那么J（R）是一水平直线或全平面ℂ－。

引理3［1］设f（z）为度大于1的多项式，则多项式f的每一个根都是Hf的（超）吸性不动点。

引理4［2］设f为多项式，g（z）＝az＋b（a≠0）为仿射变换，则g◦Hcfog◦g－1＝Hf，（c∈ℂ＼｛0｝）。

2 定理的证明

定理1的证明 如果∑（f）是有限的，由引理1知，对任意的σ∈∑（f），存在正整数k使得m为使得f表示成f（z）＝zrQ（zm）的最大整数。从而

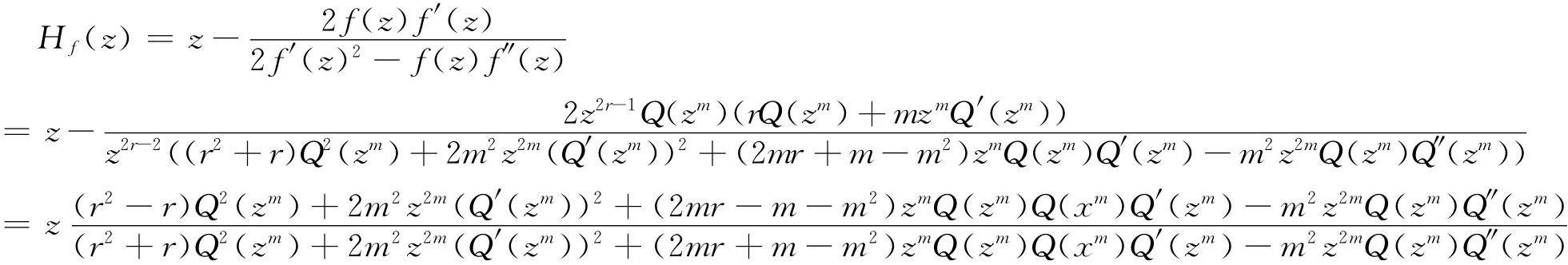
易见σ◦Hf◦σ－1（z）＝Hf（z），则σJ（Hf）＝J（Hf），从而有σ∈∑（Hf），即证

如果∑（Hf）是无限的，由引理1有f（z）＝zn，其中n＝deg（f）。从而，即知J（Hf）＝∞，显然有∑（Hf）＝｛σ∶σ（z）＝e2πθiz＋b（θ∈［0，1］）｝。注意到J（f）为单位圆周，从而∑（Hf）＝｛σ∶σ（z）＝e2πθiz（θ∈［0，1］）｝⊂∑（Hf）。

定理2的证明 当J（Hf）是一水平直线时，显然平移变换σ＝z＋1∈∑（Hf）。

如果平移变换σ＝z＋1∈∑（Hf），则Hf（z）满足引理2的条件，故J（Hf）是一水平直线或全平面，然而多项式f（z）至少有一个零点，由引理3，Hf至少有一个吸性不动点，故J（Hf）≠ℂ－，即知J（Hf）为一水平直线。

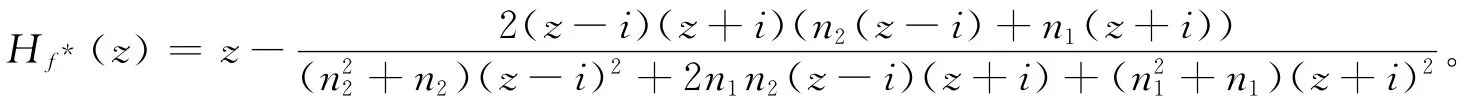
以下证明当n1≠n2时，J（Hf＊）不能为一直线。注意到

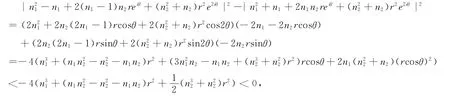
因此｜Hf＊（z）－i｜＜｜z－i｜。因为i为Hf＊的（超）吸性不动点，故｛z∶Im（z）≥3｝包含在i的所在的Fatou分支内。再注意到任意的水平线｛z∶Im（z）＝t｝∪｛∞｝在Hf＊下不是前向不变的，此时J（Hf＊）不可能为一条直线。

接下来证明当n1＝n2≜n时，J（Hf＊）为带无穷点的实轴。此时

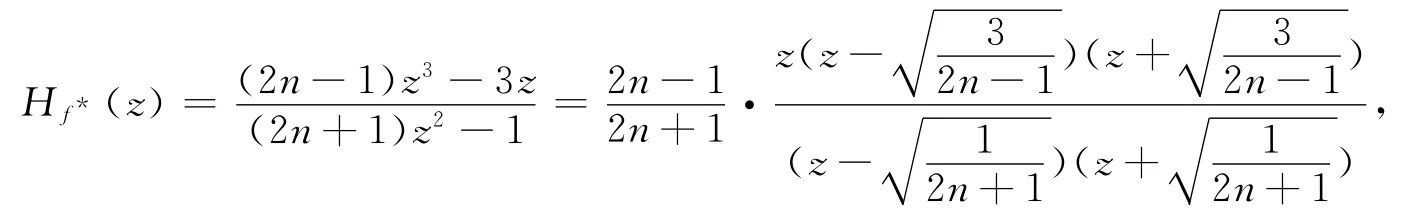
易见Hf＊（ℝ∪｛∞｝）＝ℝ∪｛∞｝。

下证Hf－1＊（ℝ∪｛∞｝）＝ℝ∪｛∞｝。因Hf＊（∞）＝∞且，故∞为Hf＊的斥性不动点，从而∞∈J（Hf＊），又由所以∈J（Hf＊）。对于任意的x，因

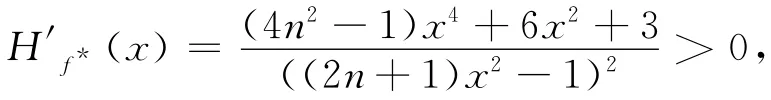
故Hf＊（x）在三个区间以及都是从－∞单调递增到0；而Hf＊（x）在三个区间以及从0单调递增到＋∞。从而对任意的x∈ℝ，H－1f＊（x）∈ℝ，可知J（Hf＊）＝ℝ∪｛∞｝.由仿射变换的性质，可知J（Hf）＝g（J（Hf＊））为连接z1与z2线段的垂直平分线。

推论1的证明 结合定理2和定理3的结论即证。

［1］Kneisl K.Julia sets for the super Newton method，Cauchy's method，and Halley's method［J］.Chaos，2001，11：359－370.

［2］Wang X Y，Yu X J.Julia sets for the standard Newton's method，Halley's method，and Schröder's method for multiple root［J］.Appl.Math.Comput.，2007，189（2）：335－338.

［3］Beardo A F.Symmetries of Julia sets［J］.Bull.London Math.Soc.，1990，22：575－582.

［4］Levin.G.Symmetries on a Julia set［J］.Adv.in Sov.Math.，1991，3：131－141.

［5］Boyd D.Translation invariant Julia sets［J］.Proc.Amer.Math.Soc.，2000，128：803－812.

［6］Yang W F.Symmetries of the Julia sets of Newton's method for multiple root［J］.Appl.Math.Comput.，2010，217（6）：2490－2494.

［7］Beardon A F.Iteration of Rational Functions［M］.Berlin：Springer，1991.

［8］乔建永.重整化变换的复动力学［M］.北京：科学出版社，2010.