利用差分模拟退火算法解决漂流调度问题
邹战勇,陆 淼,黄炜豪
(广东商学院 数学与计算科学学院,广东 广州 510320)
0 引 言
Big Long River是座落在美国的世界第四长河,游客可以到属于Big Long River的一段大长河(225英里)领略风光和令人兴奋的白色激流。这条河是进不去登山者的,因此观光只能用的方式是沿河旅行,这需要几天的露营。所有的沿河旅行都始于第一站并在下游225英里远的最终出口退出。如何安排一个最优方案使得大长河能容纳更多的船只以及船只的相遇次数达到最小是本文研究的目标。Gimblett R[1-2]使 用The Wilderness Use Simulation Model模拟户外娱乐环境中人类与环境相互作用,该模型被应用到旅行者的使用跟踪段、越野旅行路线和营地,重点是对相遇次数和活动的潜在冲突进行估计。为了最大化利用露营地,本文设计了一个漂流模拟器。它扩增了河流容纳量的同时尽可能减少船只相遇的次数。
为了尽量满足大量的漂流需求,需要决定河流的最大容纳量X′。当然,容纳量由旅行的安排方案和Y值共同决定,同时还需要减少两组的相遇,这是一个多约束的多目标规划问题。本文将给出普遍适用的优化算法,并对于不同的Y值和旅行时间,都能求出最优安排方案,使得X′达到最大,同时相遇最少。
1 模型和算法
1.1 模型的建立
根据问题分析,我们知道这是一个多约束的目标规划问题。第一目标是使得X′达到最大,第二目标是相遇最少,并满足相应的约束条件。但与一般的规划问题不同的是,影响目标的因素(旅行时间、船速和每天的航行时间)存在一定的随机不确定性。这就产生了一个非常巨大的解空间,而我们则需要在这个解空间里面寻找最优方案使得X′最大。因此我们可以运用蒙特卡洛模拟产生解空间,并利用属于智能搜索的模拟退火算法进行求解。
为了允许更多的旅行数量,设目标函数为:

约束条件:
(1)同一组露营者不能在同一个露营点露营超过一晚。
(2)两组露营者不能同时占领同一个露营点。
根据以上的约束条件,建立以下目标规划模型:
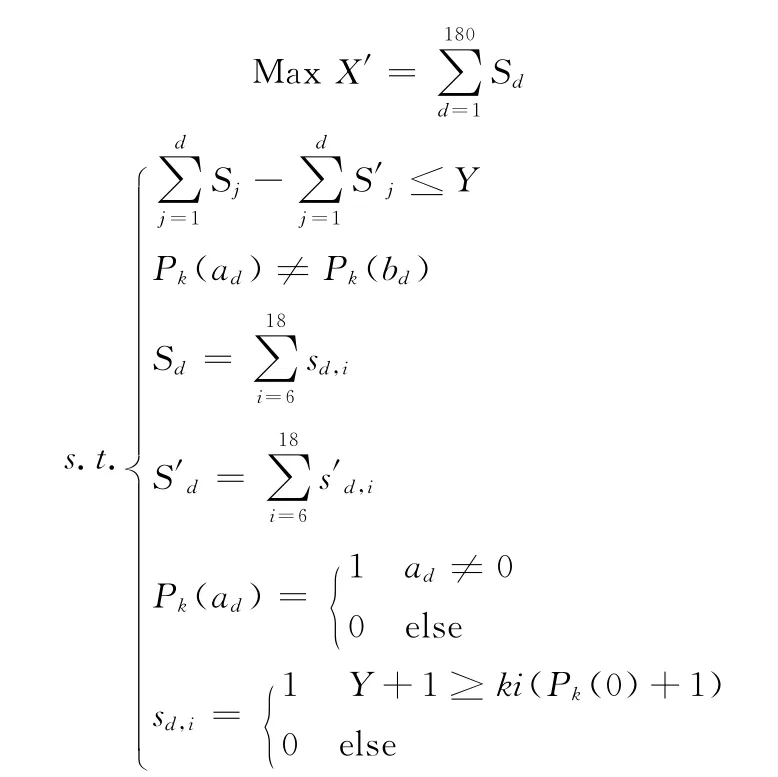
其中
Sd:第d天出发的船的总数,d=1,2,3…18
sd,i:第d天i晚旅行出发的船的数量,i=6,7,8…18
s′d,i:第d天i晚旅行出发的船的数量
Pk(ad):a号船第d天占领第k个露营点,k=1,2,3…18
1.2 模拟退火算法
模拟 退 火 算 法(Simulated Annealing,SA)[3-4]最 早 由Kirkpatrick等应用于组合优化领域,它是基于Mente-Carlo迭代求解策略的一种随机寻优算法,其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法从某一较高初温出发,伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解,即在局部最优解能概率性地跳出并最终趋于全局最优。
算法SA
(1)初始化:初始温度T(充分大),初始解状态S(是算法迭代的起点),每个T值的迭代次数L;
(2)对k=1,…,L做第(3)至第6步;
(3)产生新解S′;
(4)计算增量Δt′=C(S′)-C(S),其中C(S)为评价函数;
(5)若Δt′<0则接受S′作为新的当前解,否则以概率exp(-Δt′/T)接受S′作为新的当前解;
(6)如果满足终止条件则输出当前解作为最优解,结束程序。终止条件通常取为连续若干个新解都没有被接受时终止算法;
(7)T逐渐减少,且T->0,然后转第2步。
根据大长河的实际情况,我们设最长的旅行需要18天,故先假设Y=18。我们用利用蒙特卡洛在MATLAB进行模拟仿真求解。我们这里随机生成500个6~18天的旅行,并根据模拟退火算法从500个旅行中搜索最优的安排方案,从而求出最大X′=288,总相遇次数为767。下面三维饼状图中,从9%开始逆时针方向的各个数值分别代表6~18天旅行各占X′的比例,可以看出各个时间的旅行所占比例基本持平。
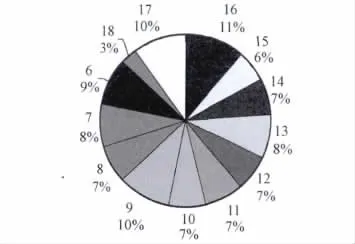
图1 16~18天旅行各占X′比例的饼状图
1.3 差分模拟退火算法
容易看出,并不是所有的组合优化问题都给出令人满意的解决方案,当问题的解很平缓时,或则很少有局部最优值,模拟退火算法将很快找到最优解或无法爬出来,考虑到模拟退火算法有可能陷入局部最优的状态(见图2),我们将借鉴差分进化算法[5-6]。差分进化算法是一种基于群体进化的算法,具有记忆个体最优解和种群内信息共享的特点,即通过种群内个体间的合作与竞争来实现对优化问题的求解,其本质是一种基于实数编码的具有保优思想的贪婪遗传算法。
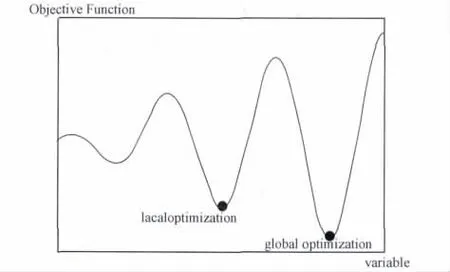
图2 最优解和局部最优解图
结合差分进化算法变异的思想和模拟退火算法,我们提出了差分模拟算法。
算法DE
求解非线性函数f(x1,x2,…,xn)的最小值问题,xi满足:
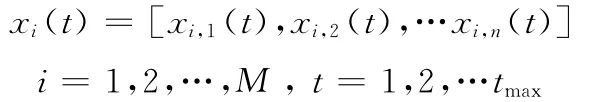
令xi(t)是第t代的第i个染色体,则xLij≤xij≤xUijj=1,2,…n
其中,n是染色体的长度,即变量的个数,M为群体规模,tmax是最大的进化代数。
第一步:生成初始种群
在n维空间里随机产生满足约束条件的染色体,实施如下措施:

第二步:变异操作
从群体中随机选择3个染色体xp1,xp2,xp3(i≠p1≠p2≠p3),则

其中,xp2j(t)-xp3j(t)为差异化向量,η为缩放因子。
根据差分模拟退火算法原理和思想,利用MATLAB编程求解,得到最优方案中X′为320,总相遇次数为925。X′比优化前的结果提高了11%(见图3和图4)。
从图3中可以看到算法DE(optimized result)露营6晚和7晚的旅行团在优化方案中增加得比较明显,这表明增加时间短的旅行团可以使X′更大。

图4显示了算法SA在30s左右时X′就到达最大值,这表明陷入局部最优解的可能性很大。优化后的算法DE虽然收敛速度相对较慢,但是我们可以得到更好的最优解X′,这表明优化后的算法的优异性。
具体的试验结果是利用算法SA的得到X′和相遇次数分别为288和767,而用算法DE求得X′=320,总相遇次数为925。这表明优化后的算法DE确实更优!
1.4 稳定性和灵敏度分析
用MATLAB在计算机上模拟了约70次,发现X′集中在305左右。模拟结果表明我们提出的模型和算法是稳定的(见图5)。
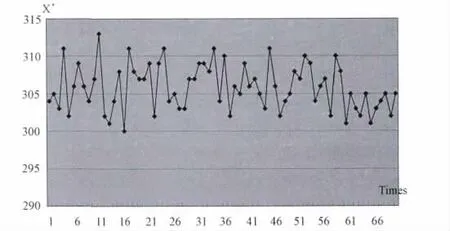
图5 模型和算法是稳定性图
我们考虑6~18天的旅行时间服从正态分布,所以用同样的方法求得此时的最优方案(见图6),其中X′=282,总相遇次数为314。结果表明,对于各种旅行时间的分布,算法都具有很强的实用性。
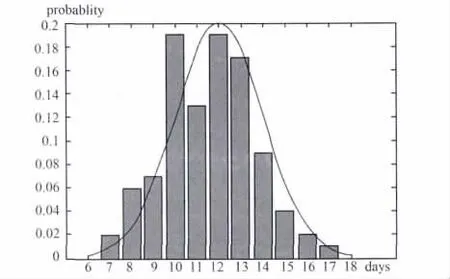
图6 旅行时间正态分布下的最优方案图
1.5 相遇次数的最小化
在第一目标的求解中,我们给出了最优的安排方案使得X′最大,并分析了算法的灵敏度和稳定性。下面我们对第二目标(相遇最少)进行分析求解。我们考虑通过合理分配摩托船或橡皮筏或通过调整同一天里不同旅行团的出发顺序,来最大限度的减少相遇次数。实际情况中我们发现6~18中平均旅行时间是12晚,如果再把摩托船或橡皮筏的船速结合取平均为6mile/h,则可以求出每组平均每天需要漂流225/(12*6)=3.125h。即我们可以把3.125h视为一种整体上的每天漂流时间的平均数,从而为不同的旅行分配合理的摩托船或橡皮筏。
根据不同的旅行时间,我们可以为不同的旅行团安排摩托船或橡皮筏。当旅行团时间为9晚时,平均每天需要漂流25miles,如果用4miles/h的橡皮筏,每天平均至少需要漂流6h。则对于旅行时间为6、7、8、9的组,他们都需要每天平均漂流6h以上,我们可以认为这样的漂流时间是过长的。所以6~9晚的旅行应该用摩托船。同样道理,当旅行时间为15晚时,如果用摩托船,则每天平均漂流1.875h,我们认为这样的漂流时间是过短的。故15~18晚旅行应该用橡皮筏(4miles/h)。故我们根据旅行团的时间得到以下安排:

表1 旅行团安排时间
在该安排方案中,我们首先找出一天内多组出发的情况。对于这一天,我们可以安排旅行时间短的组先出发,并分配合理的船。要使该方案的相遇次数尽量减少,其中原来的相遇次数为816,调整安排后为767,即相遇次数减少了6%。
我们用计算机同样进行70次模拟(见图7),平均减少约5%,说明我们的调整方法对一般安排方案的相遇次数都可以到达稳定的减少率。
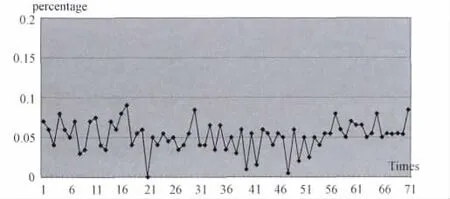
图7 模型与算法的稳定性70次模拟图
2 结论及推广
本文分别用算法SA和算法DE来求出最大化X′,结果显示优化后的算法DE优于算法SA,模型和算法对于不同的参数可以重复得到最优方案。并检验了在不同假设条件下的结果都没有对优化的结果有很大改变,数字最优化结果和分析技术的一致性表明求解的结果至少是一个局部最优解。
本文的模型和算法不仅适用于河道漂流问题,也能推广到公车、火车、飞机等调度问题。对于一般的优化问题,通常都需要从所有方案中寻求最优方案。模拟退火和差分模拟退火算法是一种启发式的智能算法,对于大规模的优化问题,其优点显著。
[1]Gimblett R,Roberts C,Daniel T,et al.An intelligent agent based model for simulating and evaluating river trip scenarios along the colorado river in Grand Canyon National Park[M].In H R Gimblett(Ed.),Integrating GIS and Agent based modeling techniques for Understanding Social and Ecological Processes,Oxford Press,2000:245-275.
[2]Gimblett,H.R.,B.Durnota,R.M.Itami.Spatially explicit autonomous agents for modeling recreation use in complex wilderness landscapes[J].Complex International Journal,1996(3):134-140.
[3]Shechter,M.,R.L.Lucus.Simulation of recreational use for park and wilderness management[M].Johns Hopkins University Press for Resources for the Future,Inc,Washington,D.C.220pp.1978.
[4]Stan,Alexandru-Ioan.Assessing inbound call center scheduling through boots trapping and DGP based monte carlo simulation[J].Review of Economic Studies &Research VirgilMadgearu,2011(3):234-240.
[5]敖友云,迟洪钦.多目标差分演化算法研究综述[J].计算机科学与探索,2009(3):234-246.
[6]刘明广.差异演化算法及其改进[J].系统工程,2005(2):108-111.

