复习教学中“一题多解”策略的运用

方阳

(长沙市雅礼中学 湖南 长沙 410007)

“一题多解”不是盲目地追求物理问题的多解，更不是学生或教师炫耀自己的解题能力．在笔者看来，“一题多解”作为高中物理总复习期间的一种复习策略，如果运用恰当，对夯实学生物理基础知识和方法，提高学生分析解决物理问题的能力大有裨益．在复习的不同阶段，应该采取不同类型的“一题多解”策略．在第一轮复习中，我们更关注学生对基础物理知识和基本方法的掌握，不急于要求学生从整体上把握高中物理知识体系．所以，针对第一轮复习的特点，我们应多采取“知识点”内的“一题多解”策略，学生从多角度思考而更全面掌握基础知识和方法．而在第二轮、第三轮复习中，我们更多地强调学生综合分析能力的提升，在这个阶段，我们就要放宽眼界，多采取“学科体系”内的“一题多解”策略，让学生从更宽广的视角思考问题，在不同思维方式的碰撞中培养物理直觉，提高综合分析能力．

1 “知识点”内的“一题多解”

这里的“知识点”，应该是我们通常说的高考要求中的一个个单独的“考点”．下面以一例题加以说明．

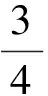
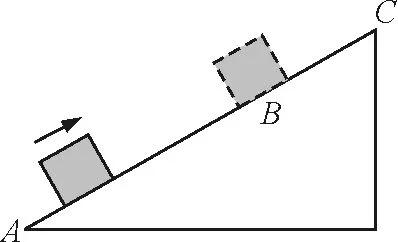
图1

解法1：一般公式法

匀减速到速度为零的直线运动可以看成逆向的初速度为零的匀加速直线运动．设AC全程位移大小为s0，物体的加速度为a，物体从B滑到C用时tBC，则对BC段和AC段分别有

(1)

(2)

由(1)、(2)两式相比，解得

tBC=t

解法2：平均速度法

AC段的平均速度为

(3)

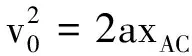
(4)

(5)

(6)

联立式(3)～(6)，可得

由此可知，B点的瞬时速度等于全程AC的平均速度，所以B点的瞬时速度就是全程中点时刻的瞬时速度，即物体从B滑到C所用的时间也为t．

解法3：位移比例法

因为，第一个T内、第二个T内、第三个T内…的位移的比为

x1∶x2∶x3∶…∶xn=1∶3∶5∶…∶(>2n-1)

现有

所以，物体运动在BC段和运动在AB段所花的时间相同，都为t．

解法4：时间比例法

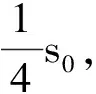
t1∶t2∶t3∶…∶tn=

所以，对AB段有

(7)

化简式(7)，得

t0=t

解法5：图像法

作物体做匀减速直线运动的v-t图像如图2．显然，只要令t=t0(t0为匀减速运动的中间时刻)．匀减速运动的前一半时间与后一半时间内的位移大小的比为3∶1．所以物体运动从B到C所花时间也为t．

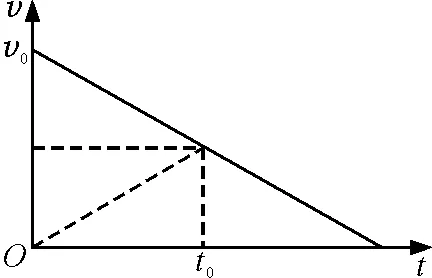
图2

点评：这道题很简单，展示的多种方法都是关于匀变速直线运动这一考点的方法，以此类题目为载体，向学生展示常用解题方法是一个很好的选择．学生通过此题的“一题多解”，在了解多种常用解题方法的基础上，对各种方法进行比较判别，体会每一种方法的特点，逐渐养成选用最佳解题方案的“物理直觉”．

图3

2 “学科体系”内的“一题多解”

这里的“学科体系”，指的是高中阶段所接触到的物理学基本体系，主要指力学、电磁学、热学、光学和原子物理的综合体系．下面以一例题加以说明．

【例2】(2007年高考江苏卷第19题)如图3所示，一轻绳吊着粗细均匀的棒，棒下端离地面高H，上端套着一个细环．棒和环的质量均为m，相互间最大静摩擦力等于滑动摩擦力kmg(k>1)．断开轻绳，棒和环自由下落．假设棒足够长，与地面发生碰撞时，触地时间极短，无动能损失．棒在整个运动过程中始终保持竖直，空气阻力不计．求：

(1)棒第一次与地面碰撞弹起上升过程中，环的加速度；

(2)从断开轻绳到棒与地面第二次碰撞的瞬间，棒运动的路程s；

(3)从断开轻绳到棒和环都静止，摩擦力对环及棒做的总功W．

解析：(1)设棒第一次上升过程中，环的加速度为a环1，环受合力为

F环=kmg-mg

(8)

由牛顿第二定律

F环=ma环

(9)

联立(8)、(9)两式得a环=(k-1)g，方向竖直向上.

(2)设以地面为零势能面，向上为正方向，棒第一次落地的速度大小为v1.

由机械能守恒

解得

设棒弹起后的加速度a棒，由牛顿第二定律

a棒=-(k+1)g

棒第一次弹起的最大高度为

解得

棒运动的路程

(3)解法1

环的速度为

棒的速度为

环的位移为

棒的位移为

x1=h环1-h棒1

解得

棒环一起下落至地，有

解得

同理，环第二次相对棒的位移为

……

环相对棒的总位移

x=x1+x2+…+xn+…

W=kmgx

得

解法2

设环相对棒滑动距离为L，根据能量守恒，得

mgH+mg(H+L)=kmgL

摩擦力对棒及环做的总功为

W=-kmgL

解得

点评：此题是一道力学综合题．在前两问通过牛顿第二定律求得棒和环的加速度以后，可以顺水推舟地通过加速度，利用匀变速直线运动规律，从运动学的角度来解答第(3)问(题中解法1)，就像我们平时所强调的那样，要注意加速度在连接动力学和运动学时的桥梁作用．但这种解法显然不是最简洁的．在系统学习完高中阶段物理学知识后，特别是在经历过了高三第一轮复习之后，在进一步复习中就要更加注重知识的综合和考虑问题的多角度性，以使学生达到融会贯通的境界，而在这一目的的达成过程中，“一题多解”不失为一种很好的策略．此题第(3)问如若从能量的角度考虑，问题解答过程非常简捷，而且物理情景也变得更为清晰简单．在“一题多解”过程中，学生在拓展自己思维角度的同时，更可以领略不同解答方法在具体问题中的优劣，久而久之，就会形成善于选择最优解答方案解题的物理直觉．