并联型储能系统孤网运行协调控制策略

彭思敏 窦真兰 凌志斌 蔡 旭,

（1.上海交通大学电子信息与电气工程学院 风力发电研究中心 上海 200240 2.上海交通大学海洋工程国家重点实验室 上海 200240）

1 引言

近年来随着能源危机、环境恶化等问题的日益加剧，风电、光伏等可再生能源（Renewable Energy Source, RES）的发展越来越受到人们的重视[1]，然而这些可再生能源因自身固有的间歇性、波动性等特点，给电力系统的稳定运行及可靠供电带来一定负面影响[2]。将这些RESs就地构成微电网进行孤网供电为解决上述问题提供了一种有效方式，尤其是偏远地区或海岛[3]。

与并网运行不同，因无大电网支撑且含间歇性、波动性 RESs及动态负荷，孤网运行时首要问题是保证系统电压幅值和频率的稳定，即维持公共母线电压幅值up和频率fp的稳定。储能系统（Battery Energy Storage System, BESS）的接入为解决这些问题提供了一种有效的方式[4,5]。

同时，在实际研究及应用中，为满足孤网中风能穿透比高或大容量负荷的要求，需要将多个BESS并联构成并联型储能系统（Parallel-Connected Battery Energy Storage System, P-BESS），但存在 RESs与P-BESS间如何协调控制、P-BESS内如何协调控制及分配负荷以维持up和fp稳定等问题。由于 RESs及P-BESS一般经电压型逆变器后并联向负载供电，又因其无互联线、可实现即插即用功能等优点，采用下垂控制策略是实现RESs与P-BESS间协调控制及分配负荷的一种有效控制方式[5-11]。文献[6, 7]从理论上分析了在不同电压等级电网中功率传输特性，并给出了适合低压微电网的功率传输特性。文献[8]针对微电网孤网运行控制，提出了基于传统下垂控制的对等控制策略。文献[9]考虑到低压微电网线路阻抗并不完全为纯感性，引入虚拟频率和电压来实现功率解耦控制，但其控制算法复杂。文献[10]以逆变器输出端电压为切入点推导了并联功率理论，提出一种基于“类功率”的无互联线并联下垂控制策略。文献[11]提出了一种自适应分布式下垂控制策略以实现微电网中并联变换器的功率平衡。上述研究主要是针对 RESs与单个 BESS并联运行控制，而对于在考虑电池系统的荷电状态[12]（State of Charge, SOC）基础上如何实现RESs与P-BESS间、P-BESS内部的协调控制及负荷分配，进而稳定up和fp的研究并不多。

本文在分析 P-BESS工作原理的基础上，根据电池系统工作特性并结合下垂控制，提出了基于电池系统SOC（SOCb）的外环负荷功率分配控制策略。同时，考虑到传统下垂控制固有的静态误差、中低压电网线路并不完全表现为纯感性等特点，提出了含线性补偿环的内环电压幅值-频率控制策略，从而使系统更加有效地进行负荷分配以实现系统功率平衡。最后，建立了系统仿真模型，并设计了实验平台。

2 P-BESS系统的构成及工作原理

2.1 P-BESS的构成

本文基于P-BESS的孤网系统结构如图1所示。孤网系统主要由P-BESS、负载、RESs及备用电源组成，且各单元交流侧并联在公共母线上。P-BESS由多个模块化BESS并联构成（单个BESS间的距离可根据实际情况而定）；每个BESS又由一个电池系统（Battery System, BS）与一个功率变换系统（Power Conversion System, PCS）组成；每个PCS主要由三相桥式电压源变换器及LCL滤波器构成，BS接入其直流母线侧；每个BS是由一定数目电池单体经串/并联直接构成。负载主要包括电机负载、RL负载等。备用电源主要包括柴油机，用于BS放电完后配合P-BESS共同向负载供电。

图1 基于并联型储能系统的孤网结构图Fig.1 An islanded power system based on P-BESS

2.2 工作原理

在孤网系统中，首先由P-BESS建立up和fp。当开关 S1断开瞬间，P-BESS将迅速承担系统中负载与RESs（如风电）之间的瞬时功率差。当负载或RESs变化时，P-BESS都根据各BESS中电池系统的SOCb初始状态，快速调节各BESS输出的有功、无功功率来平滑系统功率差，以维持up和fp的稳定。对于每个BESS而言，仅利用本地信息（电压、电流等）并通过控制PCS输出的电压幅值和相位差来维持up和fp的稳定，可实现BESS的即插即用功能。特别是当 RESs不能向孤网中负荷供电（如几小时内无风）时，P-BESS将单独为负载供电，并维持系统稳定。

3 P-BESS控制策略

为便于分析，本文以其中任一个模块化 BESS为例进行分析与研究，单个BESS的控制策略如图2所示。图中，U0、ω0分别为up及fp的给定值；Udc为电池系统端电压；Ib为电池系统输出电流。

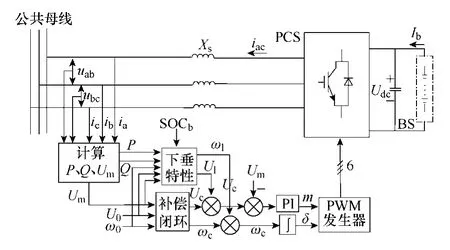
图2 BESS控制原理图Fig.2 Schematic diagram of control scheme for a BESS

P-BESS中BESS控制策略为由功率外环与电压内环构成的双环控制策略。其中功率外环控制为：通过检测每个BESS本地公共母线的线电压和相电流，计算出本地有功功率P、无功功率Q和电压幅值Um，P、Q经基于电池系统 SOCb的下垂控制分别得到相应的电压幅值Ul及角频率ωl。而电压外环控制为：将Ul及ωl分别与由线性补偿环得到的电压幅值Uc和角频率ωc进行叠加，得到给定电压幅值Ue和角频率ωe。Ue与实测的电压幅值Um的差值经比例-积分调节器后，得到调制比m；ωe直接经积分后得到相位角δ。最后将m和δ送PWM脉冲发生器产生IGBT的驱动信号，从而控制PCS的输出有功、无功功率大小和方向，实现对up和fp的稳定控制。

3.1 负荷分配协调控制

如图1所示，P-BESS包括多个BESS，孤网运行时，考虑到系统中无其他电源向负载供电，则P-BESS将承担系统中的所有负载供电（若有其他电源向负载供电，则 P-BESS将承担其他电源与负载间功率差），忽略线路中能量损耗，根据能量守恒定律得到总负载有功率Pl和无功功率Ql分别为

式中，Pi和Qi分别为第i个BESS提供的有功功率和无功功率。

根据电力系统中电压/频率下垂控制（V/f控制）特性，任意一个BESS提供的有功功率和无功功率静态特性如图3所示。

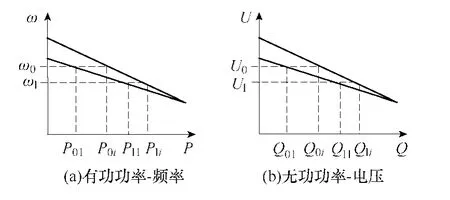
图3 有功和无功功率静态特性Fig.3 Static characteristics of active power and reactive power

与基于传统下垂特性的电压/频率控制方法类似，各个BESS输出电压/频率下垂控制特性可表示为

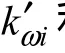
在传统电力系统中，通常以BESS中PCS额定容量来衡量 BESS额定容量，即kω′i和kvi的大小取决于每个PCS的有功、无功功率额定值为

式中，Δωmax、ΔUmax分别为可允许的最大角频率差及电压差；Psi、Qsi分别为第i个PCS的有功、无功功率额定值。

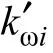
式中，kωi为第i个 BESS的有功功率下垂系数。于是，得到基于改进型下垂控制的负荷功率分配策略，即单个BESS输出有功功率/频率下垂控制特性：

由式（7）、式（8）可知，P-BESS工作过程中，在满足Pi≤Psi前提下（Pi＞Psi时，有功功率下垂系数将仍按式（5）计算，将作为后续工作进一步讨论），系统中有功负荷分配主要取决于各BESS中电池系统的SOCb比值，且跟随其变化而变化。SOCb越大，对应的BESS将发出更多的有功功率以维持系统有功功率平衡，反之，将分配较少的有功负荷。

3.2 电压及频率控制

考虑到传统下垂控制固有的静态误差、中低压电网线路并不完全表现为纯感性等问题，本文引入线性补偿环节以微调电压幅值和频率的给定值，使系统在稳定工作时静态误差为 0。图4为含线性补偿环节的电压幅值和频率控制图。

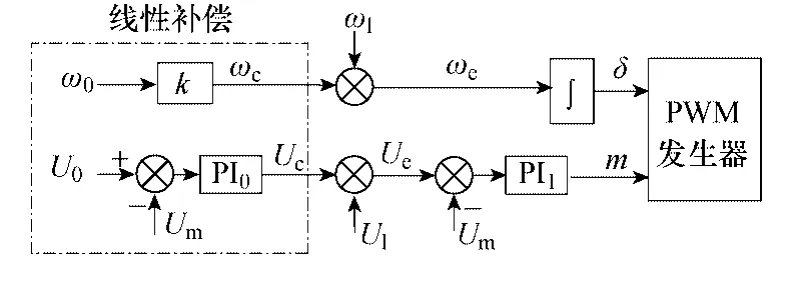
图4 电压及频率控制策略Fig.4 Control strategy of voltage and frequency

线性补偿环节主要分为两部分：一是由公共母线电压幅值给定与检测值的差值作为比例-积分调节器（PI0）的输入，得到电压补偿值Uc；二是由公共母线电压角频率给定直接经过频率补偿系数k后，产生角频率补偿值ωc。其具体表达式为

式中，kcp、kci分别为电压补偿部分调节器 PI0的比例系数和积分系数，k为频率补偿系数。

同时，含线性补偿环的电压-频率控制为

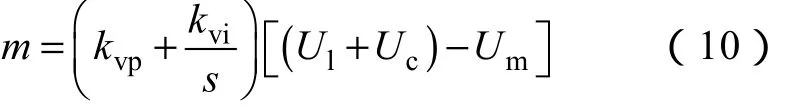
式中，kvp、kvi分别为电压环中调节器 PI1的比例系数和积分系数。

4 仿真及结果

为验证本文所提出的基于电池系统 SOCb改进下垂控制策略的正确性及电压补偿的作用，根据图1所示系统结构，在PSCAD/EMTDC电磁暂态仿真环境下搭建了由P-BESS（含有2个BESS）及不同负荷（大电动机、纯电阻负载、阻抗性负载）构成的系统仿真平台，具体系统仿真参数见下文。平台主要电源为储能系统，风电作为辅助电源，以验证在极端情况（如短时无风状态）下P-BESS中各BESS负荷分配控制及其维持系统电压幅值和频率稳定的能力。关于风电与P-BESS共同作为电源组成风-储混合系统将作为后续工作，有待进一步研究。仿真时负载变化如下：初始时刻，系统带纯电阻负载（5kW）运行一段情况；2s时刻，突然启动大电机（30kW）；4s时刻，再投入纯电阻负载（10kW）；5s时刻，再投入阻抗性负载（（10+j15）kVA）；之后，在6s、7s、9s时刻依次切除阻抗性负载、纯电阻负载、大电机等。图 5为在 2个电池系统 SOCb的初始值（SOCb1_0=0.8、SOCb2_0=1）不同时分别带不同负载情况下系统响应情况。

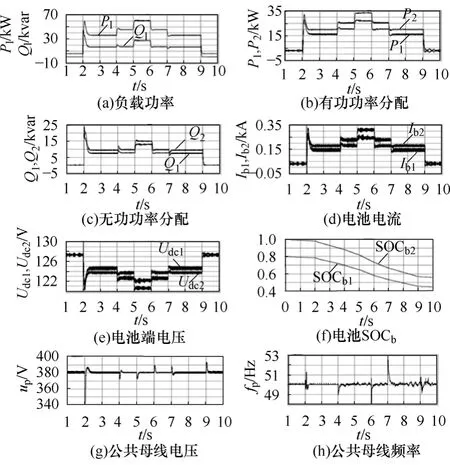
图5 SOCb1_0与SOCb2_0不同时带不同负载情况下系统响应情况Fig.5 System response to various loads when SOCb1_0 is not equal to SOCb2_0

图 5a为负载有功、无功功率变化情况。由图5b、图5c可知，无论负载的投入，还是切除，2个BESS始终都能快速跟随系统负载变化，且在系统稳定运行状态时能根据预定比值（SOCb1_0∶SOCb2_0=0.8∶1=4∶5）分配负荷有功、无功功率，而对应电池放电电流Ib1与Ib2亦按此预定比值向负载供电（见图5d）。特别地，大电机启动时（2s时刻），由于惯性作用，负载有功功率（Pl）、无功功率（Ql）迅速上升，经过一段时间（约 0.2s）后进入稳定运行状态。为维持系统功率平衡，BESS1和 BESS2均迅速调节其各自有功功率输出（P1、P2）与无功功率输出（Q1、Q2）以平滑系统功率差，且电机稳定运行时成比例（4∶5）分配负荷有功、无功功率，从而验证了基于 SOCb下垂控制策略能迅速平滑系统功率差且有效进行负荷功率分配。由图5e可知，当系统每次进入新的稳定状态后，电池端电压（Udc1、Udc2）短时内基本保持不变，即使当负载发生变化时，其端电压变化也不大，因为这是由电池电压工作特性所决定。图 5f为2个电池系统 SOC变化情况（为便于分析，仿真时电流积分常数按1∶1 000设定）。不难看出，虽然 SOCb2_0＞SOCb1_0，但因Ib2始终大于Ib1，随着SOCb1由0.8下降到0.45、SOCb2由 1下降到 0.55，而 SOCb1与 SOCb2的差值由初值0.2逐渐减少到0.1，即SOCb1与SOCb2越来越趋于相同，从而证明本文采用所提出的基于SOCb下垂控制策略有助于各电池系统间 SOCb均衡，进而有利于电池系统的管理与控制。由图 5g、图 5h可知，up和fp都一直稳定在其给定值附近，当负载突变时，up最大突变范围约为10%，而fp最大突变范围约为 6%，当系统稳定后，up波动范围小于0.1%，而fp波动范围小于0.1%，再一次验证了本文所提出控制策略具有维持系统up和fp稳定的能力。

图6 加入线性补偿环前后up及fp对比Fig.6 Comparison analysis of up and fp with added linear compensation

图6所示为加入线性补偿环前后的up及fp的对比情况。由图6可知，加入线性补偿后，无论系统负载如何变化，系统每次达到新的稳定状态后，up都能稳定在其给定值附近（380V），其最大偏离范围小于0.1%；而对补偿前的系统而言，系统负载变化时，系统每次达到新的稳定状态后，up都在一定程度上偏离其给定值，且随负载的增大而偏离程度越大，最大偏离范围约为2.6%（5s时刻）。与此同时，加入线性补偿后的fp在系统达到新的稳定状态后亦都能稳定在其给定值附近（50Hz），且其上、下波动程度较小，最大波动范围约为0.5%；而补偿前的fp在系统每次达到新的稳定状态后其上下波动程度相对大些，最大波动范围约为 1%，尤其是大电机切除后（9s时刻）。

5 实验及结果

为进一步验证本文所提出的基于电池系统SOCb改进下垂控制策略的正确性，本文设计开发了实验平台。系统主要包括P-BESS（2个BESS组成，每个BESS中包括PCS样机及BS）和负荷（1台感应电机、1台笼型电机及阻抗负载）。2个BS的SOC初值分别为 SOCb1_0=0.8、SOCb2_0=1。控制器采用TM320F2812处理器。系统具体参数见下表。

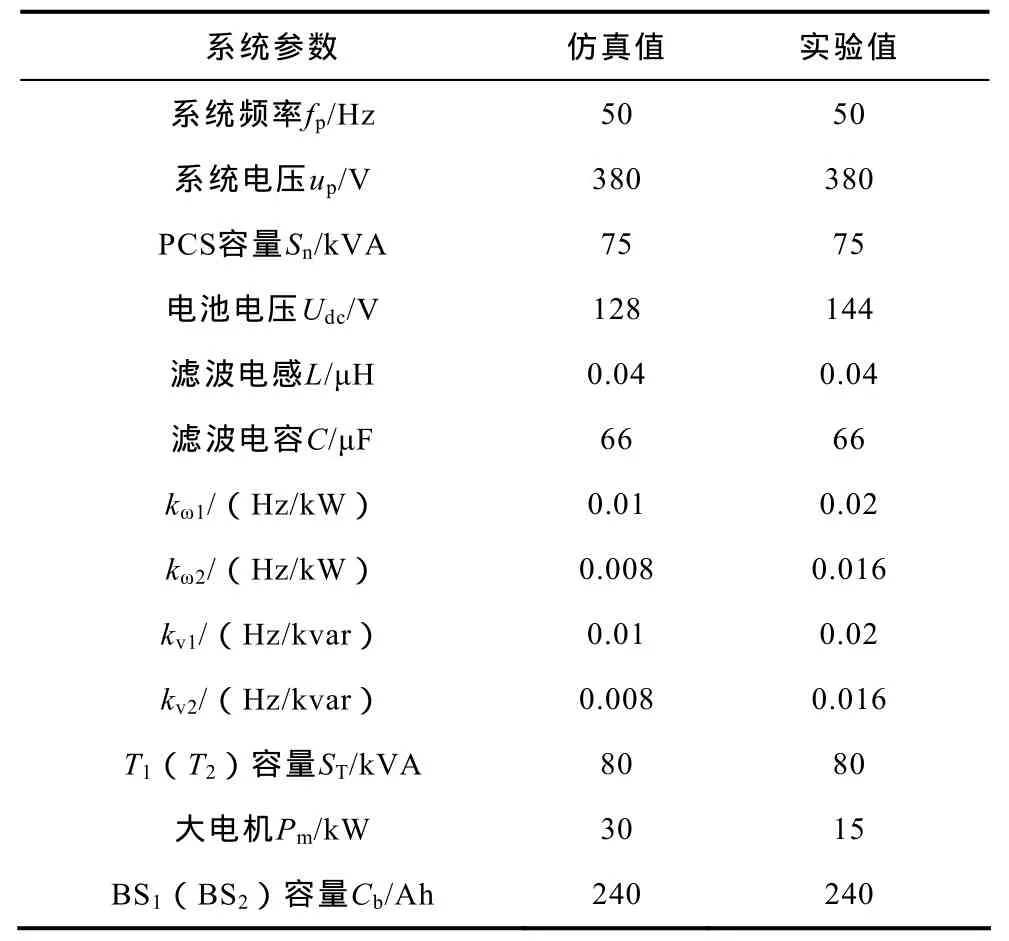
表 仿真及实验参数Tab. Parameters of simulations and experiments

图7为大电机启动时系统动态响应情况。当大电机全压启动瞬间，由于惯性作用，大电机的电流im先迅速上升，大小约为额定值的5、6倍，而后经过一段时间（约0.25s）进入稳定运行状态。为平衡系统功率，BESS1通过控制其PCS1使电池放电电流Ib1也先迅速激增而后回落到稳定状态（电池向外放电为负，下同），以快速补偿大电机启动时的系统功率差，进而维持up在其额定值 380V。同时，由于启动时间短，BESS1的电池系统端电压Udc1变化一般较慢，故先略微下降后恢复到稳定值（约140V）。

图7 大电机启动瞬间系统动态响应情况Fig.7 System dynamic response when large motor starts

图8为带大电机负载（15kW）及笼型电机负载（5.5kW）时系统稳态响应情况。由图8a可知，系统稳定时，up和fp基本稳定在额定值（380V、50Hz），且公共母电压、电流ip波形为光滑正弦波，BESS1输出电压up1亦基本维持在其额定值 70V。由图 8b可知，为维持系统有功、无功功率平衡，2个BESS在系统稳定运行状态时需根据预定比值（SOCb1_0∶SOCb2_0=4∶5）分配负荷有功功率，又因稳态时电池系统端电压（Udc1、Udc2）短时间内基本不变，所以，2个 BESS对应电池系统将按预定比值向外放电（Ib1∶Ib2≈70A∶90A≈4∶5），且电流方向一致（均为负）。同时，整个供电过程中up和fp基本稳定在额定值。

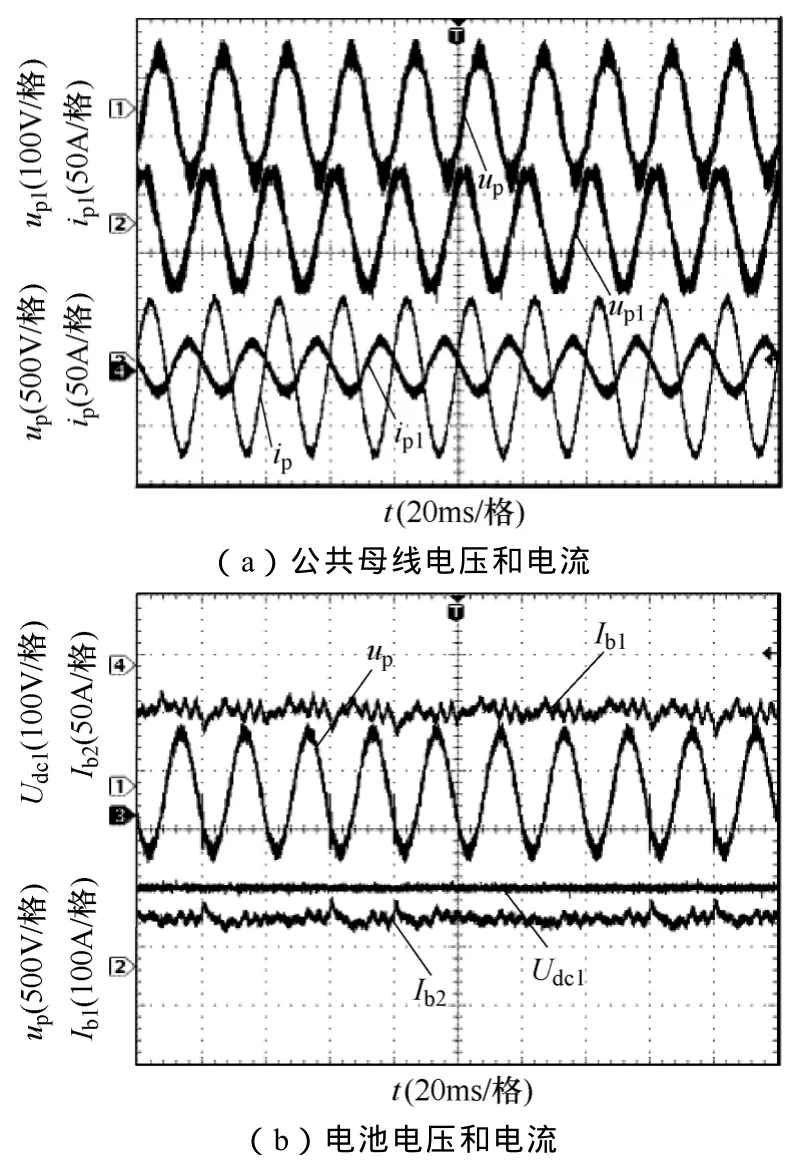
图8 带不同电机负载时系统稳态响应情况Fig.8 System steady-state response with different motors

6 结论

本文针对P-BESS孤网运行时如何实现P-BESS协调控制及负荷分配的问题，在介绍基于 P-BESS的孤网系统结构与工作原理的基础上，提出了以基于电池系统 SOCb改进型下垂控制的负荷分配控制策略为功率外环、含线性补偿环的电压-频率控制策略为电压内环的双闭环协调控制策略，并搭建了系统仿真模型及实验样机。仿真及实验结果表明，本文所提出的控制策略能根据 P-BESS中各 BESS的电池系统 SOCb初始预定比值来快速、有效地分配负荷功率，并实现系统功率平衡，进而维持系统的稳定，适宜为风能穿透比高、负载波动性大的孤岛系统供电。同时，所提出的控制策略有助于实现P-BESS中各BESS的SOCb均衡，进而提高电池系统使用寿命，为电池管理系统的设计与研究提供了一种思路。

[1] Nehrir M H, Wang C, Strunz K, et al. A review of hybrid renewable/alternative energy systems for electric power generation: configurations, control,and applications [J]. IEEE Transactions on Sustainable Energy, 2011, 2(4): 392-403.

[2] 邓自刚, 王家素, 王素玉, 等. 高温超导飞轮储能技术发展现状[J]. 电工技术学报, 2008, 23(12): 1-10.Deng Zigang, Wang Jiasu, Wang Suyu, et al. Status of highTcsuperconducting flywheel energy storage system[J]. Transactions of China Electrotechnical Society, 2008, 23(12): 1-10.

[3] 杨琦, 马世英, 李胜, 等. 微型电网运行及控制设计[J]. 电工技术学报, 2011, 26(1): 267-273.Yang Qi, Ma Shiying, Li Sheng, et al. Design of microgrid operation model and control[J]. Transactions of China Electrotechnical Society, 2011, 26(1):267-273.

[4] Perumal B V, Chatterjee J K. Voltage and frequency control of a stand alone brushless wind electric generation using generalized impedance controller[J].IEEE Transactions on Energy Conversion, 2008, 23(2): 632-641.

[5] 彭思敏, 曹云峰, 蔡旭. 大型蓄电池储能系统接入微电网方式及控制策略[J]. 电力系统自动化, 2011,35(16): 38-42.Peng Simin, Cao Yunfeng, Cai Xu. Control of large scale battery energy storage system interface to microgrid[J]. Automation of Electric Power Systems,2011, 35(16): 38-42.

[6] Engler I A. Applicability of droops in low voltage grids[J]. International Journal of Distributed Energy Resources, 2005, 1(1): 3-15.

[7] 陈达威, 朱桂萍. 低压微电网中的功率传输特性[J].电工技术学报, 2010, 25(7): 117-123.Chen Dawei, Zhu Guiping. Power tranmission charactertics of low voltage microgrids[J]. Transactions of China Electrotechnical Society, 2010, 25(7): 117-123.

[8] Lopes J A P, Moreira C L, Madureira A G. Defining control strategies for microgrids islanded operation[J]. IEEE Transaction on Power Systems, 2006, 21(2):916-924.

[9] Li Y, Li Y W. Power management of inverter interfaced autonomous microgrid based on virtual frequency-voltage frame[J]. IEEE Transactions on Smart Grid, 2011, 2(1): 30-40.

[10] 张纯江, 王晓寰, 薛海芬, 等. 微网中三相逆变器类功率下垂控制和并联系统小信号建模与分析[J].电工技术学报, 2012, 27(1): 32-39.Zhang Chunjiang, Wang Xiaohuan, Xue Haifen, et al.A quasi-power droop control of three-phase inverter and small signal modeling and analysis of parallel system in micro-grid[J]. Transactions of China Electrotechnical Society, 2012, 27(1): 32-39.

[11] Mohamed Y A R I, Saadany E F E. Adaptive Decentralized droop controller to preserve power sharing stability of paralleled inverters in distributed generation microgrids[J]. IEEE Transactions on Power Systems, 2008, 23 (6): 2806-2816.

[12] 高明煜, 何志伟, 徐杰. 基于采样点卡尔曼滤波的动力电池SOC估计[J]. 电工技术学报, 2011, 16(11):161-167.Gao Mingyu, He Zhiwei, Xu Jie. Sigma point Kalman filter based SOC esctmation for power supply battery[J]. Transactions of China Electrotechnical Society,2011, 16(11): 161-167.