基于频域分解的短期风电负荷预测

温锦斌 王 昕 李立学 郑益慧 周荔丹 邵凤鹏

（1. 上海交通大学 电工与电子技术中心 上海 200240 2. 上海交通大学 电力传输与功率变换控制教育部重点实验室 电气工程系 上海 200240 3. 吉林省电力有限公司延边供电公司 延边 133000）

1 引言

风能是理想的清洁能源，风能发电避免了火力发电对大气的污染、水力发电对生态环境的影响。随着风电技术的不断发展和风电场的规模不断增大，为了保证电力系统的稳定运行和供电可靠性，必须对风电系统进行有效的规划和调度[1]。由于风电本身所特有的间歇性和不确定性，增加了电网调度的难度，为了解决风电场的发电量不确定问题，电网必须提供足够的旋转备用容量，而旋转备用容量的增加间接地增加了风力发电的整体运营成本，所以需要对风电场的输出功率进行预测，通过对风电场发电量进行准确的预测，可以大幅降低电网旋转备用容量，从而有效降低风力发电系统的运行成本，为电网调度运行提供可靠依据[2]。

负荷预测的核心问题是预测的技术方法，或者说是预测的数学模型。随着现代科学技术的快速发展，负荷预测技术的研究在不断深化，各种各样的负荷预测方法不断涌现，从经典的单耗法[3]，统计分析法[4]，到目前的灰色预测法[5]，专家系统法[6]和模糊数学法[7]，甚至到神经网络法，优选组合法[8]和小波分析法，它们都有各自的研究特点和使用条件，也都可以应用于风电的负荷预测，在很多文献中都有详细的介绍。

上述方法都有各自的优点也有很多局限性，文献[3]提到了单耗法，单耗法在预测生产用电上的效果比较好，但不适合风电的负荷预测。文献[4]将统计分析法应用于风电负荷预测中，该方法比较适合风电负荷预测，但是需要较多的统计数据。文献[5]中提到的灰色预测法可以用少量的数据进行预测，然而预测的精度不高。近年来，由于神经网络具有以任意精度逼近输入输出间非线性关系的特性，因此在风电功率预测中得到广泛应用，但是由于风电的间歇性和不确定性，使得风电功率非常不规则，这样会使 BP网在训练中陷入局部最小，导致预测精度低。因此，如何根据风电的强随机性和不稳定特性，使用一种新的方法来提高对风电功率预测的精度，是目前特需解决的问题。

针对以上提出的问题，本文提出了一种基于频域分解的风电负荷预测方法，通过频域分解的方法，可以将无规律、随机的风电负荷曲线，分解成有不同规律的多个曲线的组合，然后对不同规律，采用不同的方法进行预测，从而提高预测的精度。该方法首先对原始数据用频域分解的方法进行分解，可以得到日周期、周周期、低频和高频四个部分，日周期的部分规律性很明显，可以用神经网络的方法训练和预测。由于风电基本没有周周期的部分，因此分解出来后，周周期的部分都是零。低频部分是非常光滑的曲线，用一元线性回归的方法预测的精度就能达到很高。高频部分规律性还是比较不明显，所以在本文中先用提升小波对其分解，可以使原来波动比较大的曲线变得比较平缓，有利于神经网络的训练和预测，大大提高了高频的预测精度。本文根据我国某风电场的真实数据，运用Matlab对其进行仿真，仿真结果表明该方法可行，具有很高的预测精度。

2 频域分解

设建模的历史负荷数据所在的时间域为D-，在制定建模时域D-的负荷时间序列P(t)可作如下傅里叶分解：

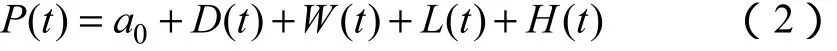
式中，日周期分量a0+D(t)和周周期分量W(t)是按固定周期变化的负荷分量；L(t)为低频分量，H(t)为高频分量。

本文中引入取模运算，用mod(m,n)表示m除以n的余数。以电力负荷日144点采样为例。

（1）D(t)的周期为144，它在负荷中以24h为周期变化的分量，a0+D(t)即为负荷的日周期分量。日周期分量a0+D(t)包括的角频率集合

（2）W(t)的周期为7×144，是负荷的周周期分量；周周期分量W(t)包括的角频率集合为

（3）去除a0，D(t)，W(t)，剩余分量可分为L(t)和H(t)。L(t)是剩余分量中低频分量的总和，它反映了气象因素等慢变相关因素对负荷的影响；H(t)是剩余分量中高频分量的总和，主要体现了负荷变化的随机性。剩余低频分量L(t)和高频分量H(t)包括的角频率集合分别为

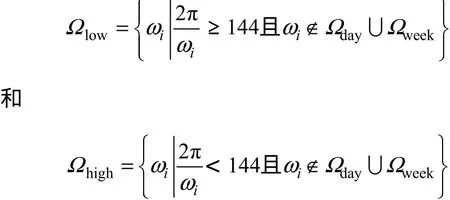
计算的目标是获得傅里叶分解后的系数ai，bi。根据傅里叶分解（级数展开）和傅里叶变换的关系，可以得到傅里叶展开的系数和傅里叶变换得到的频谱间的关系。以下是离散傅里叶变换（DFT）和离散傅里叶逆变换（IDFT）之间的变换核

根据傅里叶正变换关系，傅里叶分解后的系数ai，bi和傅里叶变换后的频谱X(ωi)之间有如下关系：

因此，对原有的负荷序列进行离散傅里叶变换后，可以由频谱值求得系数ai、bi。

但最终目的还是把原始序列分离，得到a0+D(t)，W(t)，L(t)，H(t)等四个序列，从而对预测进行评价。求得系数ai，bi后，还要进行一定的计算。

从欧拉公式 ejθ=cosθ+jsinθ入手，利用傅里叶逆变换过程，求得分解后的序列。式（4）中

根据上式的推导，可以利用傅里叶逆变换算子，求得分解后的序列。

3 提升小波

小波提升的核心就是更新算法和预测算法，通过预测算法可以得到高频信息，而通过更新算子可以得到正确的低频信息。提升样式可以实现原位计算和整数提升，并且变换的中间结果是交织排列的。其中原位计算和整数提升在硬件实现中很有价值。

3.1 小波提升的步骤

（1）分裂：分裂是将信号分割成相互关联的奇偶两部分，即ej-1（偶部分）和oj-1（奇部分）

（2）预测：预测就是用ej-1预测oj-1，实际值oj-1与预测值P(ej-1)的差值dj-1反映了两者之间的逼近程度，称为细节系数或小波系数，对应于原信号sj的高频部分。预测过程如下：

式中，预测算子P可用预测函数Pk来表示，函数Pk可取为ej-1中的对应数据本身：

或ej-1中的对应数据的相邻数据的平均值：

（3）更新：经过分裂步骤产生子集的某些整体特征可能与原始数据并不一致，为了保持原始数据的这些整体特征，需要一个更新的过程。将更新过程用算子U来代替，其过程如下：

式中，sj-1为sj的低频部分；与预测函数一样，更新算子也可以取不同函数，如

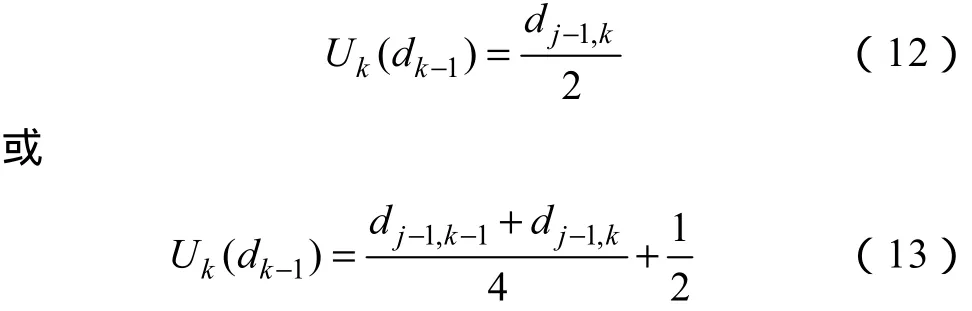
P与U取不同的函数，可构造出不同的小波变换。

3.2 分解与重构

经小波提升，可将信号分解为低频部分sj-1和高频部分dj-1；对于低频数据子集sj-1可以再进行相同的分裂、预测和更新，把sj-1进一步分解成dj-2和sj-2；…；如此下去，经过n次分解后，原始数据sj的小波表示为{sj-n,dj-n,dj-n+1, …,dj-1}。其中sj-n代表了信号的低频部分，而{dj-n,dj-n+1, …,dj-1}则是信号从低到高的高频部分系列。具体的流程图如图1所示，其中S为原始信号，A1和A2为低频信号，D1和D2为高频信号。

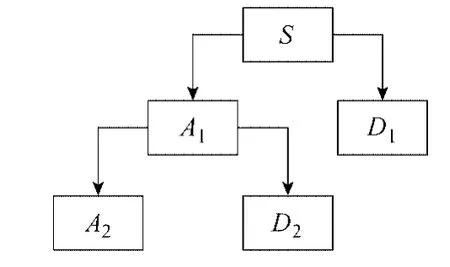
图1 提升小波分解的流程图Fig.1 The flow chart of the lifting wavelet decomposition

4 基于频域分解方法的短期风电负荷预测模型

风机的发电量受风速、风向等因素的影响，这些气象因素瞬息万变，使风电功率数据本质上具有很强的非平稳性。本文运用频域分解的方法建立短期风电负荷预测的模型，找到风电的部分规律，针对不同的特点运用不同的预测方法对其进行预测，以达到提高预测精度的目的，负荷预测的模型如图2所示。

图2 风电负荷预测模型Fig.2 Wind power load forecasting model

具体步骤如下：

（1）根据上文提到的频域分解的算法，对原始负荷序列进行频域分解，得到日周期、周周期、低频和高频四个部分。

（2）日周期部分的预测：通过频域分解后得到的日周期部分规律性非常明显，结合 BP神经网络对规律敏感的优势可以很好地来拟合该系统，跟踪效果很好。本文中采用单隐含层神经网络，网络中间层的神经元传递函数采用S型的正切传递函数，输出层神经元传递函数采用S型的对数传递函数。

（3）周周期部分的预测：由于风本身不具有周的规律性，所以风电的输出功率也不会有周的规律性，通过频域分解后得到的周周期部分全为零。

（4）低频部分的预测：通过频域分解后得到的低频部分是一段非常光滑的曲线，这样就可以运用精度非常高的一元线性回归的预测方法，即通过已知的两点预测下一点的值，令x1为已知1，x2为已知2，y为需要预测的点，公式如下：

（5）高频分量的预测：通过频域分解后得到的高频部分仍然没什么规律，但是比还没滤去日周期和低频部分的原始负荷序列平缓，有利于预测，本文将高频分量通过提升小波分解，并将其中得到的二层提升小波的低频部分输入到 BP神经网络的数学模型中训练和预测，因为经过提升小波分解后的低频部分比较平缓，可以很大程度地提高预测算法的预测精度，另外分解后得到的二层提升小波相对来说又比较细致，可以保留比较多高频分量的形状，精度更高。

5 实验结果

为了说明该方法的有效性，根据上述思想，本文选取我国北方某风电场的实际数据，建立预测的模型。本文取22天的数据，10min一个点，共1 584个点。本文中将数据分为两部分，其中前面 11天792个点作为训练样本，后面11天的792个点作为测试样本。图3为原始负荷序列。图4为通过频域分解后的四个部分。

图3 原始风电负荷序列Fig.3 The original wind power load sequence

下面首先利用前面11天792个点作为样本进行频域分解。正如上文所说，图4中日周期部分规律很明显，周周期部分全为零，低频部分是一段光滑的曲线，高频部分比较嘈杂，但是比原始序列舒缓。

图4 频域分解后的四个部分图Fig.4 The chart of four parts after frequency domain decomposition

通过运用建立的数学模型对不同的部分采用不同方法训练和预测，然后利用后面11天的792个点作为测试样本。可以分别得到预测结果图 5～图 8所示。

图5 日周期部分的预测结果图Fig.5 The chart of daily cycle part forecasting result

如图5所示，日周期部分的预测效果比较好，相对误差为5.49%。图6所示低频部分的预测效果非常好，误差非常小。图7为高频部分经过二层提升小波分解后与原高频部分的对比图，从图中可以看出，分解后的信号图和分解前的信号图是基本重合的，但是分解后的图没有了毛刺。图8是高频部分经提升小波分解后的二层小波经 BP神经网络训练和预测后的预测结果图，高频部分的预测效果也比较好，相对误差为6.25%。

图6 低频部分的预测结果图Fig.6 The chart of low frequency part forecasting result

图7 高频部分经提升小波分解后的对比图Fig.7 The comparison chart of the high-frequency part after lifting wavelet decomposition

图8 高频部分的预测结果图Fig.8 The chart of high frequency part forecasting result

各部分预测值相加就是最终的预测结果，预测值与实际值的对比如图9所示。不同预测方法的相对误差列于下表中。

图9 最后的预测结果图Fig.9 The final forecasting result chart

表 不同预测方法的相对误差Tab. The relative error of different forecasting methods

从各图和表中可以看出，通过运用频域分解的方法可以从毫无规律的风电功率中找出规律，方便用预测方法进行训练和预测，使各部分预测的精度得以提高，因此可以使最后的预测精度得到很大的提高。

6 结论

针对由风的随机性和不确定性导致的风电功率曲线的毫无规律性，建立了基于频域分解方法的风电短期负荷预测模型，在此基础上针对性地运用不同方法对频域分解出的各部分进行训练和预测，其中用了 BP神经网络、一元线性回归和提升小波与BP神经网络相结合的方法。该方法的数学模型较为简单，虽然涉及多个算法，但各算法都比较小；通过频域分解的方法可以找到一些风电负荷的规律，运用提升小波的分解可以基本去除高频部分的毛刺，这些方法都有利于预测方法的训练和预测；该模型计算速度快，最主要的相对于以往的各种方法，使风电负荷预测的精度提高到了很高的层次。

[1] 李钇里. 富锦风电场一期工程接入对黑龙江省电网的影响[J]. 黑龙江电力, 2008, 30(3): 189-191.Li Yili. Effect of connecting with power grid for first-stage construction of Fujin wind power plant on heilongjiang power grid[J]. Power of Heilongjiang,2008, 30(3):189-191.

[2] 王丽婕, 廖晓钟, 高爽. 并网型大型风电场风力发电功率-时间序列的混沌属性分析[J]. 北京理工大学学报, 2007, 27(12): 1077-1080.Wang Lijie, Liao Xiaozhong, Gao Shuang. Chaos characteristics analysis of wind power generation time series for a grid connecting wind farm [J].Transactions of Beijing Institute of Technology, 2007,27(12): 1077-1080.

[3] 王白玲. 电力负荷组合预测的理论方法及影响因素分析[D]. 北京: 华北电力大学, 2005.

[4] George Sideratos and Nikos D. Hatziargyriou. An advanced statistical method for wind power forecasting [J]. IEEE Transactions on Power Systems,2007, 22(1): 258-265.

[5] T H M El-Fouly, E F El-Saadany, M M A Salama.Grey predictor for wind energy conversion systems output power prediction[J]. IEEE Transactions on Power Systems, 2006, 21(3): 1450-1452.

[6] 于希宁，牛成林，李建强. 基于决策树和专家系统的短期电力负荷预测系统[J]. 华北电力大学学报,2005, 32 (5): 57-61.Yu Xining, Niu Chenglin, Li Jianqiang. Electric load forecast based on decision tree and expert system [J].Journal of North China Electric Power University,2005, 32 (5): 57-61.

[7] 杨期余, 汪卫华, 蓝信军. 长期电力负荷预测的模糊数学方法[J]. 湖南大学学报(自然科学版), 2002.29 (6): 67-70.Yang Qiyu, Wang Weihua, Lan Xinjun. A fuzzy mathematic method for long term load forecasting [J].Journal of Hunan University (Natural Sciences Edition), 2002, 29(6): 67-70.

[8] 赵海青. 神经网络优选组合预测模型在电力负荷预测中的应用[J]. 运筹与管理, 2005, 14 (1): 115-118.Zhao Haiqing. The application to power load forecasting of ANN optimization combinatorial predication model [J]. Operations Research and Management Science, 2005, 14(1): 115-118.

[9] J P S Catalão, H M I Pousinho, V M F Mendes.Hybrid wavelet-PSO-ANFIS approach short-term wind power forecasting in portugal [J]. IEEE Transactions on Sustainable Energy, 2011, 2(1):50-59.

[10] 庞松岭, 穆钢, 王修权, 等. 基于负荷规律性分析的支持向量机短期负荷预测方法[J]. 东北电力大学学报, 2006, 26(4): 1-6.Pang Songling, Mu Gang, Wang Xiuquan, et al. Short term load forecasting method based on load regularity analysis for supporting vector machines[J]. Journal of Northeast Dianli University Natural Science Edition,2006, 26(4): 1-6.

[11] Hans Bludszuweit, José Antonio Domínguez-Navarro,Andrés Llombart. Statistical analysis of wind power forecast error[J]. IEEE Transactions on Power Systems, 2008, 3(23):983-991.

[12] Nima Amjady, Farshid Keynia, Hamidreza Zareipour.Wind power prediction by a new forecast engine composed of modified hybrid neural network and enhanced particle swarm optimization[J]. IEEE Transactions on Sustainable Energy, 2011, 3(2):265-276.

[13] Saurabh Tewari, Charles J Geyer, Ned Mohan. A statistical model for wind power forecast error and its application to the estimation of penalties in liberalized markets[J]. IEEE Transactions on Power Systems, 2011, 26(4):2031-2039.

[14] 王丽婕, 冬雷, 廖晓钟, 等. 基于小波分析的风电场短期发电功率预测[J]. 中国电机工程学报, 2009,29(28): 30-33.Wang Lijie, Dong Lei, Liao Xiaozhong, et al. Shortterm power prediction of a wind farm based on wavelet analysis[J]. Proceedings of the CSEE, 2009,29(28): 30-33.

[15] 姜玉山, 刘嘉婧, 卢毅. 基于回归分析的频域分解短期负荷预测方法[J]. 电力需求侧管理, 2011, 13(5):12-16.Jiang Yushan, Liu Jiajing, Lu Yi. Short term load forecasting based on frequency analysis of regression[J]. Power Demand Side Management, 2011, 13(5):12-16.